a) Gọi \(ƯCLN\left(a^2,a+b\right)=d\)  với \(d\inℕ^∗\)

\(\Rightarrow\left\{{}\begin{matrix}a^2⋮d\\a+b⋮d\end{matrix}\right.\) 

\(\Rightarrow\left\{{}\begin{matrix}a^2⋮d\\a^2+ab⋮d\end{matrix}\right.\) 

\(\Rightarrow ab⋮d\) 

Vì \(a,b\) nguyên tố cùng nhau \(\Rightarrow\left[{}\begin{matrix}a⋮d\\b⋮d\end{matrix}\right.\)

Hơn nữa, vì \(a+b⋮d\) nên nếu \(a⋮d\) thì \(b⋮d\). Nếu \(b⋮d\) thì \(a⋮d\). Như vậy \(a,b⋮d\).

 Nhưng do \(a,b\) nguyên tố cùng nhau nên \(d=1\) \(\RightarrowƯCLN\left(a^2,a+b\right)=1\) hay \(a^2,a+b\) nguyên tố cùng nhau.

b) Gọi \(ƯCLN\left(ab,a+b\right)=d\)

\(\Rightarrow\left\{{}\begin{matrix}ab⋮d\\a+b⋮d\end{matrix}\right.\)

 Vì a và b nguyên tố cùng nhau nên từ \(ab⋮d\Rightarrow\left[{}\begin{matrix}a⋮d\\b⋮d\end{matrix}\right.\). Đến đây kết hợp với \(a+b⋮d\)  và lập luận tương tự như câu a), sẽ chứng minh được \(d=1\)

 Theo mình thì nó phải là ngược lại mới đúng: Tổng cạnh huyền và đường cao tương ứng luôn lớn hơn tổng hai cạnh góc vuông. (*)

 Chứng minh:

 Ta có \(AB^2+AC^2=BC^2\) (định lý Pythagoras)

\(\Leftrightarrow AB^2+2AB.AC+BC^2=BC^2+2AH.BC\)

\(\Leftrightarrow\left(AB+AC\right)^2=BC\left(2AH+BC\right)\)  

 Mà \(BC\left(2AH+BC\right)\le\left(\dfrac{BC+2AH+BC}{2}\right)^2\) \(=\left(AH+BC\right)^2\) (áp dụng bất đẳng thức  \(ab\le\left(\dfrac{a+b}{2}\right)^2\))

 Dấu "=" không thể xảy ra vì khi đó \(BC=BC+2AH\), vô lí.

 Vậy \(\left(AB+AC\right)^2=BC\left(2AH+BC\right)< \left(AH+BC\right)^2\)

 \(\Leftrightarrow AB+AC< AH+BC\). 

 Vậy (*) được chứng minh.

Ta biến đổi \(1+\dfrac{1}{\left(k-1\right)\left(k+1\right)}\) 

\(=\dfrac{\left(k-1\right)\left(k+1\right)+1}{\left(k-1\right)\left(k+1\right)}\)

\(=\dfrac{\left(k^2-1\right)+1}{\left(k-1\right)\left(k+1\right)}\)

\(=\dfrac{k^2}{\left(k-1\right)\left(k+1\right)}\) (với \(k\ge2\))

Do đó \(P=\left(1+\dfrac{1}{1.3}\right)\left(1+\dfrac{1}{2.4}\right)\left(1+\dfrac{1}{3.5}\right)...\left(1+\dfrac{1}{2020.2022}\right)\left(1+\dfrac{1}{2021.2023}\right)\)
\(P=\dfrac{2^2}{1.3}.\dfrac{3^2}{2.4}.\dfrac{4^2}{3.5}...\dfrac{2021^2}{2020.2022}.\dfrac{2022^2}{2021.2023}\)

\(P=\dfrac{2.2022}{2023}\)

\(P=\dfrac{4044}{2023}\)

Mình gửi trước câu a nhé.

a) Xét tập hợp \(A=\left\{x\inℕ|2^x\le56\right\}\). Vì A bị chặn trên nên A có phần tử lớn nhất. Giả sử \(\alpha=maxA\). Gọi \(a\) là tích của tất cả các số lẻ không vượt quá 56. Xét số \(b=2^{\alpha-1}.a\). Ta có \(b\) là bội của tất cả các phần tử của tập hợp \(\left\{2,3,4,...,56\right\}\backslash\left\{2^{\alpha}\right\}\). Do đó:

 \(b.B=\dfrac{b}{2}+\dfrac{b}{3}+...+\dfrac{b}{2^{\alpha}}+...+\dfrac{b}{56}\notinℤ\)

 Vậy B không thể là số nguyên. Ta có đpcm.

 Trước khi xem lời giải của mình thì bạn chú ý là trong đó có sử dụng những kí hiệu, thuật ngữ và tính chất khá khó hiểu với học sinh cấp II (thậm chí một vài bạn cấp III cũng chưa chắc đã hiểu thấu). Vì vậy nếu có gì khúc mắc trong lời giải thì bạn cứ nhắn tin riêng cho mình nhé. 

 Trước hết ta đến với các định nghĩa sau:

 Định nghĩa 1: Với điểm X nằm ngoài đường tròn (I), kí hiệu \(d_X\) là đường thẳng nối 2 tiếp điểm của 2 tiếp tuyến qua X ứng với (I).

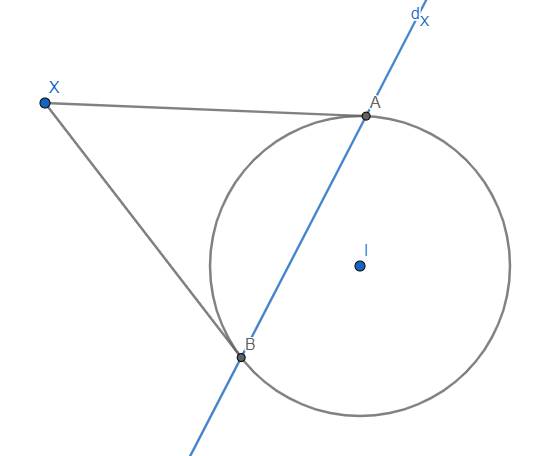
 Định nghĩa 2: Còn với điểm (I) nằm trong đường tròn, nếu lấy điểm Y trên tia IX mà \(IY.IX=R^2\) thì d_X lại là đường thẳng qua Y và vuông góc với IX.

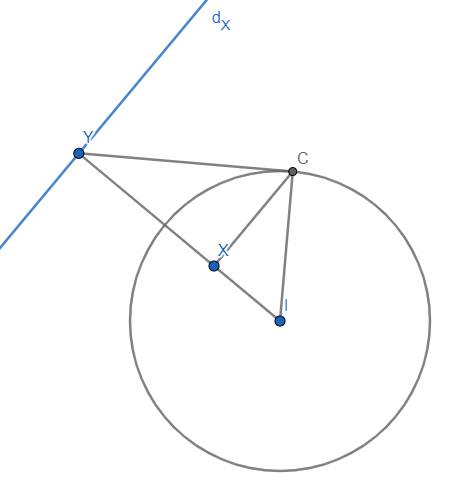
 Định nghĩa 3: Bốn điểm A, B, C, D theo thứ tự nằm trên 1 đường thẳng mà thỏa mãn \(\dfrac{AB}{AD}=\dfrac{CB}{CD}\) thì ta kí hiệu \(\left(BDCA\right)=-1\) và nếu lấy một điểm O bất kì nằm ngoài đường thẳng đó thì ta kí hiệu \(O\left(BDCA\right)=\left(OB,OD,OC,OA\right)=-1\)

 Sau đây là một số tính chất: 

 Tính chất 1: \(d_X\perp IX\), hiển nhiên.

 Tính chất 2: \(Y\in d_X\Leftrightarrow X\in d_Y\) , cũng quá hiển nhiên.

 Tính chất 3: Từ một điểm X nằm ngoài I, vẽ cát tuyến XUV với U, V thuộc (I). Khi đó một điểm Y bất kì thuộc cát tuyến này mà thỏa mãn \(\left(UVYX\right)=-1\) \(\Leftrightarrow Y\in d_X\). 

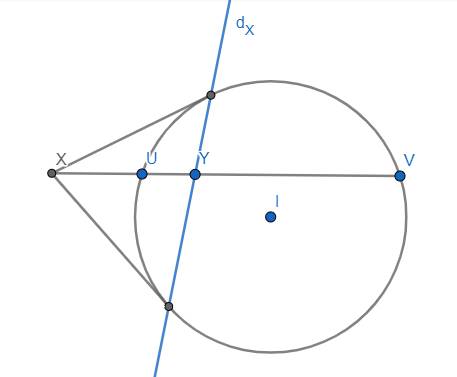
 Tính chất 4: Cho 4 điểm A, B, C, D theo thứ tự nằm trên đường thẳng d thỏa mãn \(\left(BDCA\right)=-1\) và 1 điểm O nằm ngoài d. Khi đó nếu vẽ 1 đường thẳng d' khác d cắt OA, OB, OC, OD lần lượt tại A', B', C', D' thì \(\left(B'D'C'A'\right)=-1\)

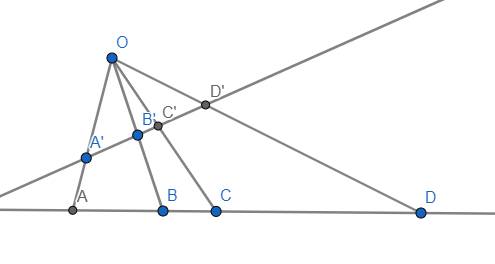
 Tính chất 5: Cho 4 điểm A, B, C, D nằm trên d và một điểm O nằm ngoài d. Khi đó kẻ một đường thẳng song song với một đường bất kì trong số OA, OB, OC, OD và cắt 3 đường còn lại tại M, N, P (N nằm giữa M và P). Khi đó M là trung điểm của NP \(\Leftrightarrow\left(BDCA\right)=-1\)

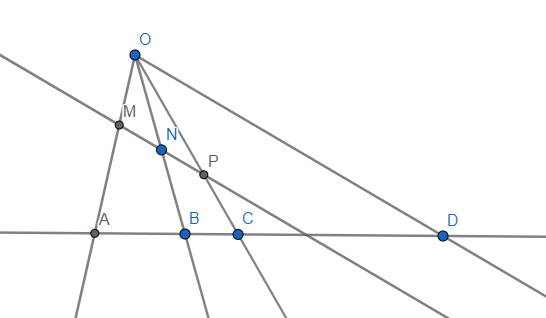
 Quay trở lại bài toán chính.

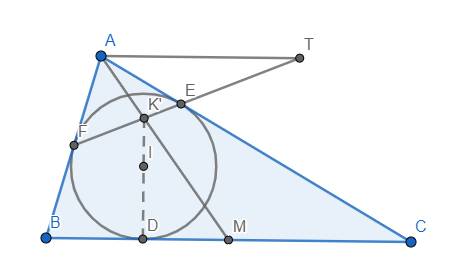
 Gọi M là trung điểm BC, K' là giao điểm của AM và EF. Qua A kẻ đường thẳng song song với BC cắt EF tại T.

 Ta sẽ chứng minh \(K'\equiv K\) hay D, E, K' thẳng hàng.

 Thật vậy, vì AT//BC và M là trung điểm BC nên theo tính chất 5\(\left(AB,AC,AM,AT\right)=-1\). Áp dụng tính chất 4, ta được \(\left(EFK'T\right)=-1\), điều này có nghĩa là \(T\in d_{K'}\) do tính chất 3.

 Hơn nữa, \(K'\in EF\equiv d_A\) nên \(A\in d_{K'}\) (tính chất 2). Do đó \(AT\equiv d_{K'}\) dẫn đến \(IK'\perp AT\) (tính chất 1).

 Do AT//BC nên \(IK'\perp BC\). Mà \(ID\perp BC\) nên D, I, K' thẳng hàng hay \(K'\equiv K\). Ta có đpcm. 

Nếu \(a=b=c=d=0\) thì nó đâu thỏa mãn đâu bạn?

À bài đó mình nhầm đề. Bài này phải làm như sau:

Ta thấy \(p^2+2q=10\)

\(\Leftrightarrow q=\dfrac{10-p^2}{2}\) \(\Rightarrow p\) chẵn

Có thế thấy nếu ta thay bất kì \(p\) chẵn nào thì đều tìm được \(q\) thỏa mãn. Chẳng hạn:

 \(\left(p,q\right)\in\left\{\left(0,5\right),\left(\pm2,3\right),\left(\pm4,-3\right),\left(\pm6,-13\right),...\right\}\)

 Ta thấy \(p^2+2q=10\)

\(\Rightarrow p\) chẵn \(\Rightarrow p=2\) \(\Rightarrow2^2+2q=10\) \(\Rightarrow q=3\), nhận.

 Vậy \(\left(p,q\right)=\left(2,3\right)\)

a) \(C=\left\{1,2,3,...,20\right\}\) hay \(C=\left\{n\inℕ^∗|n\le20\right\}\)

b) Số phần tử của không gian mẫu \(\left|\Omega\right|=20\)

Gọi A là biến cố: "Số được rút ra là số chia cho 2 và 3 đều có số dư là 1."

 Xét số \(a\) bất kì thỏa mãn \(a\equiv1\left[2\right]\) và \(a\equiv1\left[3\right]\). Khi đó \(a-1⋮2\) và \(a-1⋮3\). Do \(ƯCLN\left(2,3\right)=1\)  nên từ đây suy ra \(a-1⋮6\) hay \(a\equiv1\left[6\right]\).

 Ngược lại, nếu \(a\equiv1\left[6\right]\) thì \(a=6b+1\left(b\inℕ\right)\). Khi đó vì \(6b⋮2,6b⋮3\) nên \(a=6b+1\equiv1\left[2\right],\equiv1\left[3\right]\)

 Như vậy, \(\left\{{}\begin{matrix}a\equiv1\left[2\right]\\a\equiv1\left[3\right]\end{matrix}\right.\Leftrightarrow a\equiv1\left[6\right]\)

 Do đó biến cố A tương đương với biến cố: "Số được rút ra chia 6 dư 1".

 Khi đó các kết quả thuận lợi cho A là \(1,7,13,19\)

 \(\Rightarrow\left|A\right|=4\)

 \(\Rightarrow P\left(A\right)=\dfrac{\left|A\right|}{\left|\Omega\right|}=\dfrac{4}{20}=\dfrac{1}{5}\)

Ta thấy \(10^2!=100!=1.2.3...100\) nên có chữ số tận cùng là 0.