a) Thay hoành độ và tung độ của A vào 2 pt đường thẳng (d₁) và (d₂), ta lần lượt được:

 \(1=3\left(-1\right)+4\) (luôn đúng)

 \(-1-2.1=0\) (vô lí)

Như vậy, \(A\in d_1;A\notin d_2\)

b) Gọi giao điểm của d₁, d₂ là \(B\left(x_0;y_0\right)\). Khi đó \(x_0,y_0\) là các số thỏa mãn \(\left\{{}\begin{matrix}y_0=3x_0+4\\x_0-2y_0=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}y_0=6y_0+4\\x_0=2y_0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}y_0=-\dfrac{4}{5}\\x_0=-\dfrac{8}{5}\end{matrix}\right.\)

Vậy giao điểm của d₁ và d₂ là \(B\left(-\dfrac{8}{5};-\dfrac{4}{5}\right)\)

c) Để đường thẳng d₁, d₂, d₃ đồng quy thì d₃ phải đi qua giao điểm của d₁ và d₂. Nói cách khác, d₃ phải đi qua điểm \(B\left(-\dfrac{8}{5};-\dfrac{4}{5}\right)\)

\(\Leftrightarrow\left(m-1\right).\dfrac{-8}{5}+\left(m-2\right).\dfrac{-4}{5}+m+1=0\)

\(\Leftrightarrow\dfrac{21}{5}-\dfrac{7}{5}m=0\)

\(\Leftrightarrow m=3\)

Vậy \(m=3\) thỏa mãn ycbt.

 Gọi 2 số nguyên tố đó là p, q và giả sử \(p>q\). Khi đó ta có \(p+q,p-q\) đều là các số nguyên tố.

 Nếu \(p-q=2\) \(\Rightarrow p+q=2\) (vì \(\left(p-q\right)+\left(p+q\right)=2p⋮2\)), vô lí

 Tương tự với TH \(p+q=2\) cũng sẽ dẫn tới điều vô lí.

 Do đó \(p+q,p-q\) lẻ, mà p và q đều các số nguyên tố \(\Rightarrow q=2\)

 Vậy, ta cần tìm p để \(p\pm2\) là các số nguyên tố \(\Rightarrow p\ge5\)

 Xét \(p=5\) thì \(p+2=7;p-2=3\) thỏa mãn.

 Xét \(p>5\) thì p có dạng \(p=6k+1,p=6k+5\left(k\ge1\right)\), khi đó dễ thấy rằng \(p+2,p-2\) là hợp số, vô lí.

 Vậy \(p=5,q=2\) là cặp số nguyên tố duy nhất thỏa mãn đề bài.

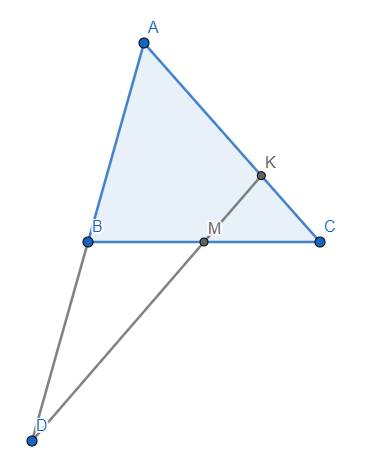
 Bài này có thể giải bằng cách dùng định lý Menelaus khá ngắn như sau:

 Áp dụng định lý Menelaus cho tam giác ABC với cát tuyến DMK, ta có: \(\dfrac{MB}{MC}.\dfrac{KC}{KA}.\dfrac{DA}{AB}=1\) \(\Rightarrow1.\dfrac{KC}{KA}.2=1\) \(\Leftrightarrow\dfrac{KC}{KA}=\dfrac{1}{2}\) \(\Leftrightarrow KA=2KC\) (đpcm)

 Nhưng nếu bạn chưa được dùng định lý Menelaus thì sẽ phải làm như sau:

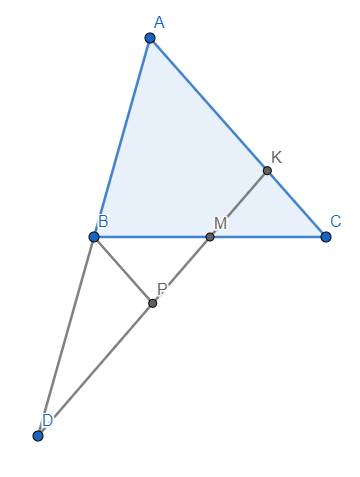
 Kẻ BP//AC \(\left(P\in DK\right)\). Khi đó theo định lý Thales, \(\dfrac{MB}{MC}=\dfrac{BP}{CK}\) và \(\dfrac{DA}{DB}=\dfrac{AK}{BP}\). Do đó:

 \(\dfrac{MB}{MC}.\dfrac{KC}{KA}.\dfrac{DA}{DB}=\dfrac{BP}{CK}.\dfrac{CK}{AK}.\dfrac{AK}{BP}=1\), và tới đây ta lại quay về tính như đã trình bày ở trên.

 Ta nhận thấy tổng các hệ số của pt bậc 2 đã cho là \(1-a+a-1=0\) nên pt này có 1 nghiệm là 1, nghiệm kia là \(a-1\), nhưng do không được giải pt nên ta sẽ làm theo cách sau:

 Ta thấy pt này luôn có 2 nghiệm phân biệt. Theo hệ thức Viète:

 \(\left\{{}\begin{matrix}x_1+x_2=a\\x_1x_2=a-1\end{matrix}\right.\)

 Vậy, \(M=\dfrac{3\left(x_1^2+x_2^2\right)-3}{x_1x_2\left(x_1+x_2\right)}\)

\(M=\dfrac{3\left[\left(x_1+x_2\right)^2-2x_1x_2\right]-3}{a\left(a-1\right)}\)

\(M=\dfrac{3\left(a^2-2\left(a-1\right)\right)-3}{a\left(a-1\right)}\)

\(M=\dfrac{3\left[\left(a-1\right)^2-1\right]}{a\left(a-1\right)}\)

\(M=\dfrac{3a\left(a+2\right)}{a\left(a-1\right)}\)

\(M=\dfrac{3a+6}{a-1}\)

b) Ta có \(P=\left(x_1+x_2\right)^2-2x_1x_2=a^2-2\left(a-1\right)=\left(a-1\right)^2\ge0\)

Dấu "=" xảy ra \(\Leftrightarrow a=1\). Vậy để P đạt GTNN thì \(a=1\)

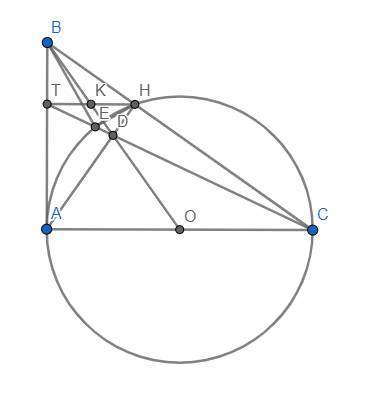
 Gọi T là giao điểm của CD và AB. Khi đó xét tứ giác ACHT, ta có:

O (trung điểm AC), D (giao điểm của 2 đường chéo) và B (giao điểm của 2 đường thẳng chứa 2 cạnh đối) thẳng hàng nên ACHT là hình thang. (bổ đề hình thang quen thuộc)

 \(\Rightarrow\) HT//AC \(\Rightarrow\) H, K, T thẳng hàng.

 Lại có \(\widehat{CEH}=\widehat{CAH}\) (góc nội tiếp cùng chắn cung AH)

 Mà \(\widehat{CAH}=\widehat{B}\) (cùng phụ với góc C)

 \(\Rightarrow\widehat{CEH}=\widehat{B}\)

 \(\Rightarrow\) Tứ giác BTEH nội tiếp \(\Rightarrow\widehat{BEH}=\widehat{BTH}\)

Mà \(\widehat{BTH}=90^o\) nên \(\widehat{BEH}=90^o\). Ta có đpcm.

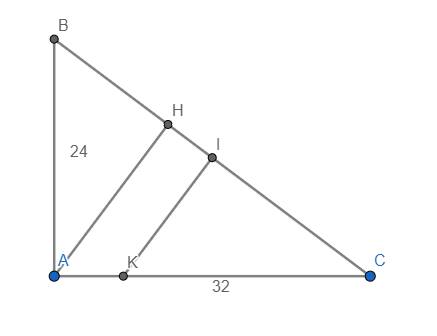
Ta có \(\widehat{HAC}=\widehat{B}\) (cùng phụ với \(\widehat{C}\)) 

Mà \(\widehat{B}=\tan^{-1}\left(\dfrac{AC}{AB}\right)=\tan^{-1}\left(\dfrac{32}{24}\right)=\tan^{-1}\left(\dfrac{4}{3}\right)\approx53,13^o\)

Nên \(\widehat{HAC}\approx53,13^o\)

Ta có \(BC=\sqrt{AB^2+AC^2}=\sqrt{24^2+32^2}=40\) cm

\(\Rightarrow IB=IC=20cm\)

Ta có \(CH=\dfrac{AC^2}{BC}=\dfrac{32^2}{40}=25,6cm\) 

\(AH=\dfrac{AB.AC}{BC}=\dfrac{24.32}{40}=19,2cm\)

Do vậy \(\dfrac{CI}{CH}=\dfrac{IK}{AH}\Rightarrow IK=\dfrac{CI.AH}{CH}=\dfrac{20.19,2}{25,6}=15cm\)

Mặt khác \(\dfrac{CI}{CH}=\dfrac{CK}{CA}\Rightarrow CK=\dfrac{CI.CA}{CH}=\dfrac{20.32}{25,6}=25cm\)

\(\Rightarrow C_{CIK}=CI+CK+IK\) \(=20+15+25=60cm\)

Mặt khác, \(S_{ABC}=\dfrac{1}{2}AB.AC=\dfrac{1}{2}.24.32=384cm^2\)

Lại có \(\Delta CIK~\Delta CAB\left(g.g\right)\) \(\Rightarrow\dfrac{S_{CIK}}{S_{CAB}}=\left(\dfrac{IK}{AB}\right)^2=\left(\dfrac{15}{24}\right)^2=\dfrac{25}{64}\)

\(\Rightarrow S_{CIK}=\dfrac{25}{64}S_{CAB}=\dfrac{25}{64}.384=150cm^2\)

a) Tứ giác BCDE nội tiếp nên \(\widehat{ABD}=\widehat{ACE}\). Từ đó dễ dàng chứng minh \(\Delta ABD~\Delta ACE\left(g.g\right)\) \(\Rightarrow\dfrac{AB}{AC}=\dfrac{AD}{AE}\) \(\Rightarrow AD.AC=AB.AE\) (đpcm)

b) Đường tròn (O) có đường kính BC nên \(\widehat{BEC}=\widehat{BDC}=90^o\) (góc nội tiếp chắn nửa đường tròn)

 \(\Rightarrow BD\perp AC,CE\perp AB\) \(\Rightarrow\) H là trực tâm tam giác ABC

 \(\Rightarrow AH\perp BC\) (đpcm)

c) Hạ \(HS\perp AO\) tại S. \(\Rightarrow S\in\left(AH\right)\). Khi đó tứ giác OKHS nội tiếp nên \(AS.AO=AH.AK=AD.AC=AN^2\) .

 Từ đây dễ dàng chứng minh \(\Delta ASN~\Delta ANO\left(c.g.c\right)\) \(\Rightarrow\widehat{ASN}=\widehat{ANO}\). Ta có \(\widehat{ANO}=90^o\Rightarrow\widehat{ASN}=90^o\) hay \(SN\perp AO\) tại S

 Hoàn toàn tương tự, ta chứng minh được \(SM\perp AO\) tại S

 Lại có \(HS\perp AO\) tại S nên H, M, N thẳng hàng (đpcm).

a) PTHH \(S+O_2\underrightarrow{t^o}SO_2\)

b) Khí SO₂ chính là chất làm cho chuột chết. Hợp chất này tên là lưu huỳnh đi-ô-xít (tên Tiếng Anh là sulfur dioxide). Đây là một oxit axit. 

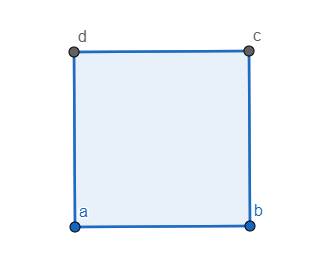
 Xét 1 mặt bất kì của khối lập phương như hình vẽ và gọi 4 số ở đỉnh là a, b, c, d. Khi đó do \(a+b+c,b+c+d,c+d+a,d+a+b\ge10\) nên \(3\left(a+b+c+d\right)\ge40\) \(\Rightarrow a+b+c+d\ge14\)

 Làm tương tự cho 4 mặt còn lại, ta đều được tổng của 4 số trên mỗi mặt đều không nhỏ hơn 14.

 Nhưng trong một mặt, sẽ có mặt có chứa đỉnh mang số 8. Khi đó 3 đỉnh còn lại bắt buộc là 1, 2, 3, mà \(1+2+3< 10\), vô lí. Lập luận tương tự cho trường hợp GTNN là 15, 16, 17. Nếu GTNN là 18, ta chỉ ra 1 trường hợp dấu "=" xảy ra:

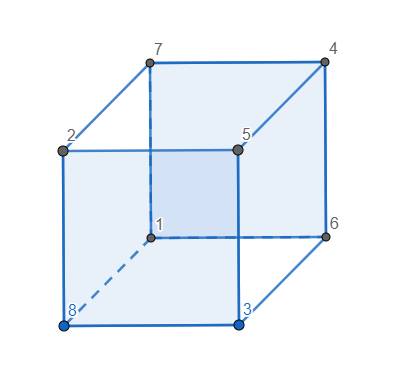
Vậy GTNN của 4 số trong cùng 1 mặt là 18.

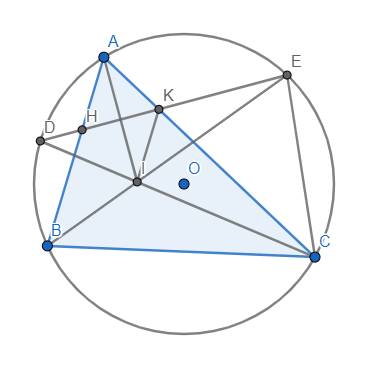
a) Ta có \(\widehat{AHK}=\dfrac{sđ\stackrel\frown{AE}+sđ\stackrel\frown{BD}}{2}\) 

và \(\widehat{AKH}=\dfrac{sđ\stackrel\frown{CE}+sđ\stackrel\frown{AD}}{2}\)

 Mặt khác, do D, E lần lượt là điểm chính giữa của cung AB, AC nên \(sđ\stackrel\frown{AD}=sđ\stackrel\frown{BD};sđ\stackrel\frown{AE}=sđ\stackrel\frown{CE}\). Từ đó \(\Rightarrow\widehat{AHK}=\widehat{AKH}\) hay tam giác AHK cân tại A (đpcm).

 b) Hiển nhiên I là tâm đường tròn nội tiếp tam giác ABC \(\Rightarrow\) AI là tia phân giác của \(\widehat{BAC}\) (hay chính là \(\widehat{HAK}\)). Mà theo câu a), tam giác AHK cân tại A nên AI đồng thời là đường cao của tam giác AHK \(\Rightarrow AI\perp HK\) hay \(AI\perp DE\) (đpcm)

 c) Ta có \(\widehat{CIE}=\dfrac{sđ\stackrel\frown{CE}+sđ\stackrel\frown{BD}}{2}\)

\(=\dfrac{sđ\stackrel\frown{CE}+sđ\stackrel\frown{AD}}{2}\) \(=\widehat{CKE}\)  nên tứ giác CEKI nội tiếp 

 \(\Rightarrow\widehat{HKI}=\widehat{DCE}\) \(=\dfrac{sđ\stackrel\frown{DE}}{2}\) 

\(=\dfrac{sđ\stackrel\frown{DA}+sđ\stackrel\frown{AE}}{2}\)  \(=\dfrac{sđ\stackrel\frown{BD}+sđ\stackrel\frown{AE}}{2}\)  \(=\widehat{AHK}\)

Từ đó dễ dàng suy ra KI//AH hay KI//AB (đpcm)