Nãy mình nhìn nhầm đề, xin lỗi bạn nhiều. Cách trình bày vẫn như vậy nhé.

Sửa lại đề chỗ kia là \(\dfrac{b}{a}\) chứ không phải \(\dfrac{b}{b}\) nhé.

Đặt \(\dfrac{a}{b}=t>0\) . Khi đó BĐT cần chứng minh tương đương:

\(t^2+\dfrac{1}{t^2}\ge t+\dfrac{1}{t}\) 

\(\Leftrightarrow t^2+\dfrac{1}{t^2}+2\ge t+\dfrac{1}{t}+2\)

\(\Leftrightarrow\left(t+\dfrac{1}{t}\right)^2\ge t+\dfrac{1}{t}+2\) (*)

Đặt \(u=t+\dfrac{1}{t}\left(u\ge2\right)\), khi đó (*) tương đương:

\(u^2-u-2\ge0\)

\(\Leftrightarrow u^2+u-2u-2\ge0\)

\(\Leftrightarrow u\left(u+1\right)-2\left(u+1\right)\ge0\)

\(\Leftrightarrow\left(u+1\right)\left(u-2\right)\ge0\) (luôn đúng vì \(u\ge2\))

Dấu "=" xảy ra \(\Leftrightarrow u=2\) \(\Leftrightarrow t+\dfrac{1}{t}=2\) \(\Leftrightarrow t=1\) \(\Leftrightarrow a=b\)

Vậy ta có đpcm.

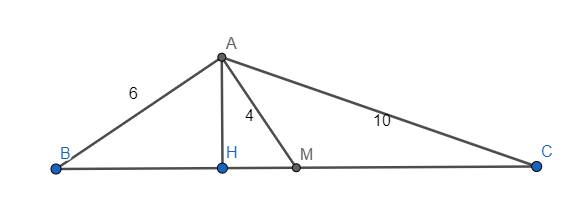
Hạ \(AH\perp BC\) tại H. Đặt \(MB=MC=x;HM=y;AH=h\)

Theo định lý Pythagoras: \(\left\{{}\begin{matrix}AH^2+HM^2=AM^2\\AH^2+BH^2=AB^2\\AH^2+CH^2=AC^2\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}h^2+y^2=16\\h^2+\left(x-y\right)^2=36\\h^2+\left(x+y\right)^2=100\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}h^2+y^2=16\\h^2+x^2+y^2-2xy=36\\h^2+x^2+y^2+2xy=100\end{matrix}\right.\)

Cộng theo vế của 2 pt thứ 2 và thứ 3 của hệ này, ta được:

\(2\left(h^2+x^2+y^2\right)=136\)

\(\Leftrightarrow x^2+\left(h^2+y^2\right)=68\)

\(\Leftrightarrow x^2+16=68\)

\(\Leftrightarrow x^2=52\) hay \(BM^2=52\)

Mà ta lại có \(AB^2+AM^2=6^2+4^2=52\)

\(\Rightarrow AB^2+AM^2=BM^2\) \(\Rightarrow\Delta ABM\) vuông tại A \(\Rightarrow\) đpcm

d) Áp dụng tính chất 2 tiếp tuyến cắt nhau trong đường tròn (O) và 2 tiếp tuyến tại M và N, ta có AO là tia phân giác của \(\widehat{MAN}\) (1)

 Lại có \(\widehat{AME}=\widehat{MNE}\) (do chúng là góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp chắn cung đó)

 Hơn nữa, vì AO là trung trực của đoạn MN nên E thuộc trung trực của MN \(\Rightarrow EM=EN\) \(\Rightarrow\Delta EMN\) cân tại E \(\Rightarrow\widehat{ENM}=\widehat{EMN}\)

 Từ đó suy ra \(\widehat{AME}=\widehat{EMN}\) hay ME là tia phân giác của \(\widehat{AMN}\). (2)

 Từ (1) và (2) \(\Rightarrow\) đpcm.

e) Gọi C là giao điểm của PO và (AMN). Khi đó ta có  \(PB^2=PN.PM=PC.PO\) nên \(\Delta PBC~\Delta POB\left(c.g.c\right)\) \(\Rightarrow\widehat{PCB}=\widehat{PBO}=90^o\) \(\Rightarrow PC\perp BC\)

Mặt khác, do đường tròn (AMN) có đường kính là AO nên \(\widehat{ACO}=90^o\Rightarrow AC\perp PC\)

 Từ đó suy ra A, B, C thẳng hàng. Do đó \(\widehat{ABM}=\widehat{BPO}\) (vì cùng phụ với \(\widehat{POB}\))

Tổng trên sẽ bằng:

 \(\left(70000+1\right).70000:2=70001.35000⋮100\)

Vậy ta có đpcm.

 Trong 1 giờ, đội A làm được \(\dfrac{1}{12}\) đoạn đường, đội B được \(\dfrac{1}{15}\) đoạn đường, đội C được \(\dfrac{1}{17}\) đoạn đường còn đội D được \(\dfrac{1}{19}\) đoạn đường.

 Như vậy, trong 1 giờ, cả 4 đội cùng làm thì được \(\dfrac{1}{12}+\dfrac{1}{15}+\dfrac{1}{17}+\dfrac{1}{19}=\dfrac{1689}{6460}\) đoạn đường. Do đó, để hoàn thành đoạn đường thì cả 4 đội cùng làm một lúc hết \(\dfrac{6460}{1689}\) giờ. 

 Xét câu A, hiển nhiên khi \(n\rightarrow+\infty\) thì \(a_n=\sqrt{n^3+n}\rightarrow+\infty\) nên dãy (a_n) không bị chặn.

 Ở câu C, lấy n chẵn và cho \(n\rightarrow+\infty\) thì dãy (c_n) cũng sẽ tiến tới \(+\infty\). Do đó dãy (c_n) cũng là 1 dãy không bị chặn.

 Ở câu B, ta xét hàm số \(f\left(x\right)=x^2+\dfrac{1}{x}\) trên \(\left[1;+\infty\right]\), ta thấy \(f'\left(x\right)=2x-\dfrac{1}{x^2}\) \(=\dfrac{2x^3-1}{x^2}\) \(=\dfrac{x^3+x^3-1}{x^2}>0,\forall x\ge1\) . Do đó \(f\left(x\right)\) đồng biến trên \(\left[1;+\infty\right]\) và do đó cũng đồng biến trên \(ℕ^∗\). Nói cách khác, (b_n) là dãy tăng . Như vậy, nếu b_n bị chặn thì tồn tại giới hạn hữu hạn. Giả sử \(\lim\limits_{n\rightarrow+\infty}b_n=L>1\). Chuyển qua giới hạn, ta được \(L=\lim\limits_{n\rightarrow+\infty}\left(n^2+\dfrac{1}{n}\right)=+\infty\), vô lí. Vậy (b_n) không bị chặn trên.

 Còn lại câu D. Ta thấy với \(n\inℕ^∗\) thì hiển nhiên \(d_n>0\). Ta thấy \(d_n=\dfrac{3n}{n^3+2}=\dfrac{3n}{n^3+1+1}\le\dfrac{3n}{3\sqrt[3]{n^3.1.1}}=1\), với mọi \(n\inℕ^∗\). Vậy, (d_n) bị chặn 

 \(\Rightarrow\) Chọn D.

 Ta nhận thấy một số có tận cùng là \(x\) thì khi lũy thừa lên mũ \(4k+1\left(k\inℕ\right)\) thì số nhận được cũng sẽ có tận cùng là \(x\). (*)

 Thật vậy, giả sử \(N=\overline{a_0a_1a_2...a_n}\). Khi đó \(N^{4k+1}=\left(\overline{a_0a_1a_2...a_n}\right)^{4k+1}\) \(=\left(\overline{a_0a_1a_2...a_{n-1}0}+a_n\right)^{4k+1}\) \(=a_n^{4k+1}\) nên ta chỉ cần xét số dư của các số từ 0 đến 9 lũy thừa với số mũ \(4k+1\).

 Dễ nhận thấy nếu \(a_n\in\left\{0,1,5,6\right\}\) thì \(a_n^{4k+1}\) sẽ có chữ số tận cùng là \(a_n\).

 Nếu \(a_n\in\left\{3,7,9\right\}\) thì để ý rằng \(3^4=9^2=81;7^4=2401\) đều có tận cùng là 1 nên hiển nhiên \(a_n^{4k}=\left(a_n^4\right)^k\) có tận cùng là 1. Do đó nếu nhân thêm \(a_n\) thì \(a_n^{4k+1}\) có chữ số tận cùng là \(a_n\).

 Nếu \(a_n\in\left\{2,4,8\right\}\) thì do \(2^4=16;4^4=256;8^4=4096\) đều có chữ số tận cùng là 6 \(\Rightarrow a_n^{4k}\) có chữ số tận cùng là 6. Khi nhân thêm \(a_n\) vào thì bộ \(\left(a_n;a_n^{4k+1}\right)\) sẽ là \(\left(2;2\right);\left(4;4\right);\left(8;8\right)\). 

 Vậy (*) đã được chứng minh.

 \(\Rightarrow\) S có chữ số tận cùng là \(2+3+4+...+4\) (tới đây bạn chỉ cần đếm xem có bao nhiêu trong mỗi chữ số từ 0 đến 9 xuất hiện trong tổng trên là xong nhé)

\(a_n^{4k}\)

Ta có \(111...11+444...44+1\) 

          100cs         50cs

\(=\dfrac{1}{9}.999...99+\dfrac{4}{9}.999...99+1\)

         100cs             50cs

\(=\dfrac{10^{100}-1}{9}+\dfrac{4\left(10^{50}-1\right)}{9}+1\)

\(=\dfrac{10^{100}-1+4.10^{50}-4+9}{9}\)

\(=\dfrac{10^{100}+4.10^{50}+4}{9}\)

\(=\left(\dfrac{10^{50}+2}{3}\right)^2\)

 Vì \(10^{50}+2\) có tổng các chữ số là 3 nên \(\dfrac{10^{50}+2}{3}\inℕ\). Vậy ta có đpcm.

 Ta có \(2\overrightarrow{MA}-3\overrightarrow{MB}=\overrightarrow{0}\) \(\Leftrightarrow\overrightarrow{MA}=\dfrac{3}{2}\overrightarrow{MB}\) . Điểm này có thể dựng được dễ dàng bằng cách lấy trên đường thẳng AB điểm M sao cho M không nằm giữa đoạn thẳng AB và thỏa mãn \(MA=\dfrac{3}{2}MB\)

Với điểm Q bất kì, ta có \(2\overrightarrow{QA}=2\overrightarrow{QM}+2\overrightarrow{MA}\) và \(3\overrightarrow{QB}=3\overrightarrow{QM}+3\overrightarrow{MB}\) nên:

\(2\overrightarrow{QA}-3\overrightarrow{QB}=-\overrightarrow{QM}+\left(2\overrightarrow{MA}-3\overrightarrow{MB}\right)\) \(=-\overrightarrow{QM}\) (do \(2\overrightarrow{MA}-3\overrightarrow{MB}=\overrightarrow{0}\)

Ta có đpcm.