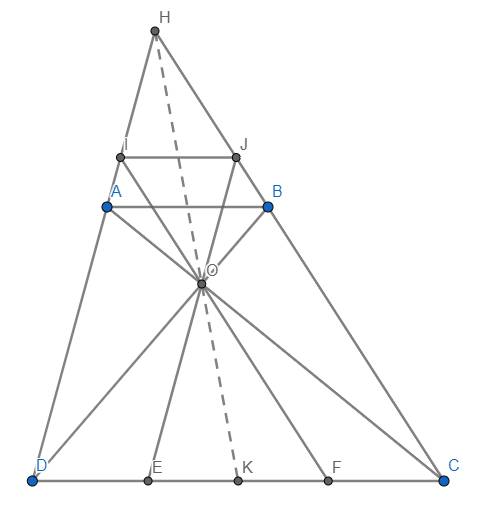
b) Theo Thales: \(\dfrac{DE}{DC}=\dfrac{AO}{AC};\dfrac{CF}{CD}=\dfrac{BO}{BD}\)

Theo câu a thì \(\dfrac{AO}{AC}=\dfrac{BO}{BD}\) \(\Rightarrow\dfrac{DE}{DC}=\dfrac{CF}{CD}\Rightarrow DE=CF\) (đpcm)

c) Từ \(DE=CF\Rightarrow\dfrac{DE}{EF}=\dfrac{CF}{EF}\)

Mà theo Thales: \(\dfrac{DE}{EF}=\dfrac{IO}{OF};\dfrac{CF}{EF}=\dfrac{JO}{OE}\) 

Do đó \(\dfrac{IO}{OF}=\dfrac{JO}{OE}\) \(\Rightarrow\) IJ//CD//AB

d) Dùng định lý Menelaus đảo nhé bạn. Ta có \(\dfrac{HA}{HD}=\dfrac{AB}{CD}=\dfrac{OA}{OC}\) nê \(\dfrac{HA}{AD}.\dfrac{OC}{OA}=1\). Do K là trung điểm EF mà \(DE=CF\) nên K cũng là trung điểm CD hay \(\dfrac{KD}{KC}=1\). Do đó \(\dfrac{HA}{AD}.\dfrac{KD}{KC}.\dfrac{OC}{OA}=1\). Theo định lý Menalaus đảo \(\Rightarrow\)H, O, K thẳng hàng (đpcm)

 Từ công thức \(F_A=d.V\), do 2 vật có cùng V và cùng ngâm trong nước (d bằng nhau) nên lực đẩy Archimèdes tác dụng lên 2 vật cũng bằng nhau.

9. D (HAppy, MENtal, PUBlic, reMOTE)

10. Unknown underline parts

11. C (the word "since" help identifying the present perfect tense)

12. C (the word "last" help identifying the past simpe tense)

13. A (the word "today" help identifying the present continous tense)

14. C (refers to an action that happened in the past which was caused by objective reasons)

15. D (adjectives always stand before nouns in a noun phrase)

16. A (base on the meaning of the word)

 February 23rd is Saturday -> February 29th is Friday (since this is a leap year) -> March 1st is again Saturday -> March 23rd is Sunday.

Có \(\overrightarrow{MA}+k\overrightarrow{MB}+\left(1-k\right)\overrightarrow{MC}=\overrightarrow{0}\)

\(\Leftrightarrow\left(\overrightarrow{MA}+\overrightarrow{MC}\right)+k\left(\overrightarrow{MB}-\overrightarrow{MC}\right)=\overrightarrow{0}\)       (1)

Gọi N là trung điểm của AC thì 

(1) \(\Leftrightarrow2\overrightarrow{MN}+k\overrightarrow{CB}=\overrightarrow{0}\)

\(\Leftrightarrow\overrightarrow{NM}=\dfrac{k}{2}\overrightarrow{CB}\)      (2)

Vậy điểm M là điểm thỏa mãn \(\overrightarrow{NM}=\dfrac{k}{2}\overrightarrow{CB}\) với N là trung điểm AC.

Choose A

-> To put a large amount of information on a map, a variety of symbols are used.

Gọi \(x,y,z,t\) lần lượt là số học sinh khối 6, 7, 8, 9.

Theo đề bài, ta có:

\(\left\{{}\begin{matrix}y+z+t=930\\x+z+t=980\\x+y+t=970\\x+y+z=960\end{matrix}\right.\)

Cộng theo vế cả 4 pt trên, thu được

\(3\left(x+y+z+t\right)=3840\)

\(\Leftrightarrow x+y+z+t=1280\)

Do đó \(x=1280-\left(y+z+t\right)=1280-930=350\)

\(y=1280-\left(x+z+t\right)=1280-980=300\)

\(z=1280-\left(x+y+t\right)=1280-970=310\)

\(t=1280-\left(x+y+z\right)=1280-960=320\)

Trước tiên, ta chứng minh \(\dfrac{1}{a}+\dfrac{1}{b}\ge\dfrac{4}{a+b}\) với \(a,b>0\) (*)

(*) \(\Leftrightarrow\dfrac{a+b}{ab}\ge\dfrac{4}{a+b}\)

\(\Leftrightarrow\left(a+b\right)^2\ge4ab\)

\(\Leftrightarrow a^2+2ab+b^2\ge4ab\)

\(\Leftrightarrow a^2-2ab+b^2\ge0\)

\(\Leftrightarrow\left(a-b\right)^2\ge0\), luôn đúng.

Vậy (*) được chứng minh. Dấu "=" xảy ra \(\Leftrightarrow a=b\) 

\(\Rightarrow VT=a+b+\dfrac{1}{a}+\dfrac{1}{b}\ge a+b+\dfrac{4}{a+b}\)

Đặt \(a+b=t\left(0< t\le\dfrac{1}{2}\right)\)thì

\(VT\ge t+\dfrac{4}{t}\) \(=t+\dfrac{1}{4t}+\dfrac{15}{4t}\)  (1)

Bây giờ ta sẽ chứng minh \(a+b\ge2\sqrt{ab}\) với \(a,b>0\) (**)

(**) \(\Leftrightarrow a-2\sqrt{ab}+b\ge0\)

\(\Leftrightarrow\left(\sqrt{a}\right)^2-2\sqrt{a}\sqrt{b}+\left(\sqrt{b}\right)^2\ge0\)

\(\Leftrightarrow\left(\sqrt{a}-\sqrt{b}\right)^2\ge0\) (luôn đúng)

Vậy (**) được chứng minh. Dấu "=" xảy ra \(\Leftrightarrow a=b\)

Do đó từ (1) \(\Rightarrow VT\ge\left(t+\dfrac{1}{4t}\right)+\dfrac{15}{4t}\) 

\(\ge2\sqrt{t.\dfrac{1}{4}t}+\dfrac{15}{4.\dfrac{1}{2}}\) (do \(0< t\le\dfrac{1}{2}\))

\(=\dfrac{17}{2}\)

Dấu "=" xảy ra \(\Leftrightarrow\left\{{}\begin{matrix}t=a+b=\dfrac{1}{2}\\a=b\end{matrix}\right.\Leftrightarrow a=b=\dfrac{1}{4}\)

Ta có đpcm.

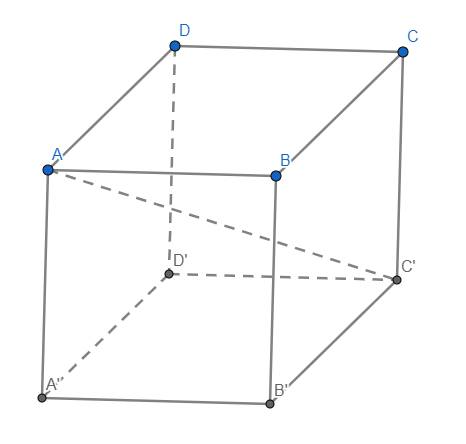
Ta có \(3AB^2=AC'^2=9a^2\) \(\Leftrightarrow AB^2=3a^2\Leftrightarrow AB=a\sqrt{3}\)

\(\Rightarrow V_{hlp}=AB^3=3a^3\sqrt{3}\) (đơn vị thể tích)

Điều kiện đã cho \(\Leftrightarrow7\left(x-2019\right)^2+y^2=23\) (*)

Do \(\left(x-2019\right)^2,y^2\ge0\) nên (*) suy ra \(y^2\le23\Leftrightarrow y^2\in\left\{0,1,4,9,16\right\}\)

\(\Leftrightarrow y\in\left\{0,1,2,3,4\right\}\)

Hơn nữa, lại có \(y^2=23-7\left(x-2019\right)^2\). Ta thấy \(VP\) chia 7 dư 2.

\(\Rightarrow y^2\) chia 7 dư 2 \(\Rightarrow y\in\left\{3,4\right\}\)

Xét \(y=3\) \(\Rightarrow7\left(x-2019\right)^2=14\) \(\Leftrightarrow\left(x-2019\right)^2=2\), vô lí.

Xét \(y=4\Rightarrow7\left(x-2019\right)^2=7\) \(\Leftrightarrow\left(x-2019\right)^2=1\) \(\Leftrightarrow\left[{}\begin{matrix}x=2020\\x=2018\end{matrix}\right.\)

Vậy \(\left(x,y\right)\in\left\{\left(4;2020\right),\left(4;2018\right)\right\}\) thỏa mãn ycbt.