Chỗ này mình sửa lại nhé.

 Vẽ đường tròn (C) có tâm D bất kì. Với một điểm X nằm ngoài đường tròn (C), kí hiệu \(d_X\) chính là đường thẳng nối 2 tiếp điểm của 2 tiếp tuyến kẻ từ D với (C)

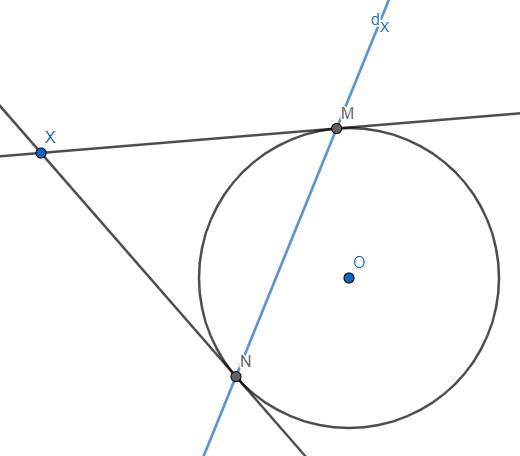
 Còn với điểm X nằm trong đường tròn, lúc này ta lại chọn 1 điểm Y nằm trên DX sao cho \(OX.OY=R^2\) (R là bán kính của (C)) thì ta định nghĩa d_X là đường thẳng qua Y và vuông góc với OX.

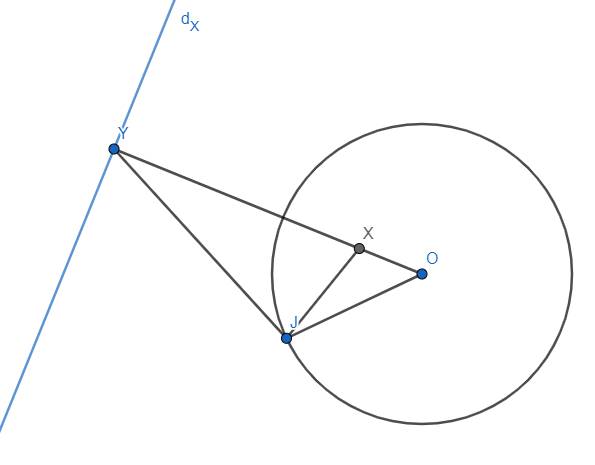
Từ các định nghĩa trên, hiển nhiên \(X\in d_Y\Leftrightarrow Y\in d_X\)

Ta có một bổ đề quan trọng sau:

Bổ đề 1: 3 điểm X, Y, Z thẳng hàng \(\Leftrightarrow\) d_X, d_Y, d_Z đồng quy.

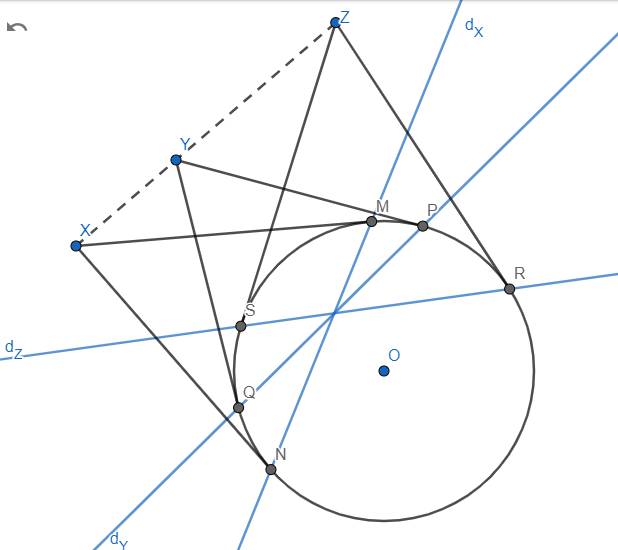
 Chứng minh: Giả sử có X, Y, Z thẳng hàng. Gọi T là giao điểm của \(d_X,d_Y\). Khi đó \(T\in d_X\Leftrightarrow X\in d_T\). Tương tự thì \(Y\in d_T\) \(\Rightarrow XY\equiv d_T\). Thế nhưng do X, Y, Z thẳng hàng \(\Rightarrow Z\in d_T\Leftrightarrow T\in d_Z\). Vậy d_X, d_Y, d_Z đồng quy tại T.

 Ngược lại, giả sử d_X, d_Y, d_Z đồng quy tại T. Đương nhiên khi đó \(T\in d_X,d_Y,d_Z\)  nên \(X,Y,Z\in d_T\) hay X, Y, Z thẳng hàng.

 Vậy bổ đề 1 được chứng minh.

 Trở lại bài toán chính.

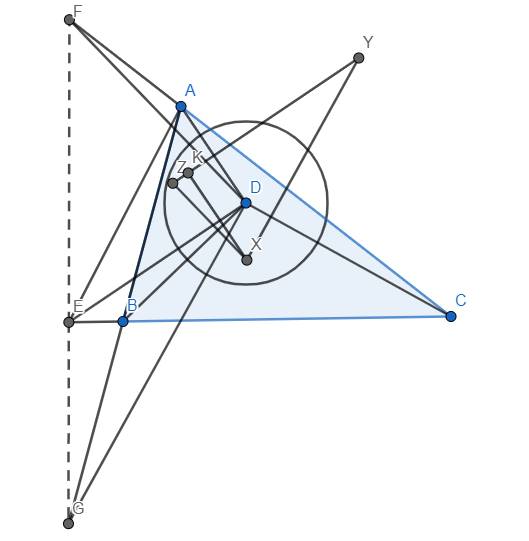
 Ta có E, B, C thẳng hàng nên theo bổ đề 1, d_E, d_B, d_C đồng quy tại X. Tương tự, d_F, d_C, d_A đồng quy tại Y và d_G, d_A, d_B đồng quy tại Z.

 Hơn nữa, \(d_E\perp DE,d_A\perp DA,DA\perp DE\) nên \(d_X\perp d_A\). Suy ra d_E là đường cao kẻ từ A' của tam giác A'B'C'. Tương tự suy ra d_E, d_F, d_G đồng quy tại trực tâm của tam giác A'B'C'.

 Lại theo bổ đề 1 \(\Rightarrow\) E, F, G thẳng hàng. (đpcm)

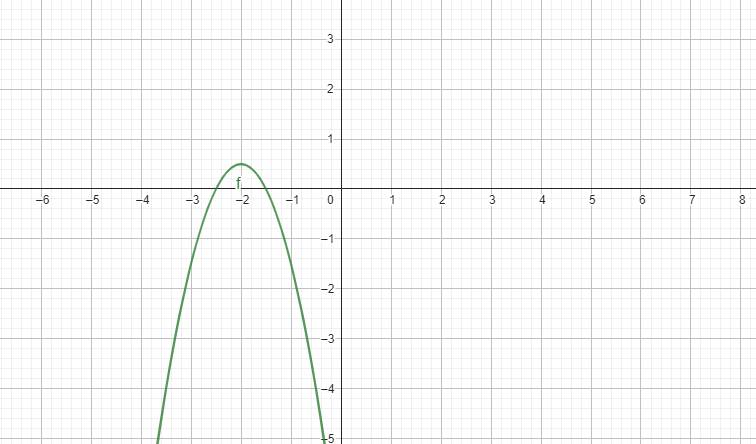
 Xét parabol \(\left(C_m\right):y=-2x^2-\left(2m-1\right)x+6-3m\), ta có \(\Delta=\left[-\left(2m-1\right)\right]^2-4\left(-2\right)\left(6+3m\right)=4m^2+20m+49\)

  Gọi \(I_m\) là đỉnh của \(\left(C_m\right)\) thì \(I_m\left(\dfrac{-2m+1}{4};\dfrac{4m^2+20m+49}{8}\right)\)

  Để hàm số đã cho nghịch biến trong khoảng \(\left(-2;+\infty\right)\) thì \(\dfrac{-2m+1}{4}=-2\Leftrightarrow m=\dfrac{9}{2}\)

a) Khối lượng nước cần đun \(m=DV=2,5.1=2,5\left(kg\right)\)

Nhiệt lượng \(Q_{nc}=mc\Delta t=2,5.4200.80=840000\left(J\right)\)

Công suất \(P=\dfrac{Q_{nc}}{t}=\dfrac{840000}{14.60+35}=960\left(W\right)\)

Hiệu suất của bếp là \(H\%=\dfrac{P}{P_{tp}}.100\%=\dfrac{960}{1000}.100\%=96\%\)

b) Điện năng tiêu thụ trong 1 ngày là \(Q'=\dfrac{2Q}{H}=\dfrac{2.840000}{0,96}=1750000\left(J\right)\)

Nhiệt lượng cần dùng trong 30 ngày là \(Q_{tp}=1750000.30=52500000\left(J\right)\) \(=14,583\left(kWh\right)\)

Số tiền điện phải đóng là \(Q_{tp}.800=21875\) (đồng)

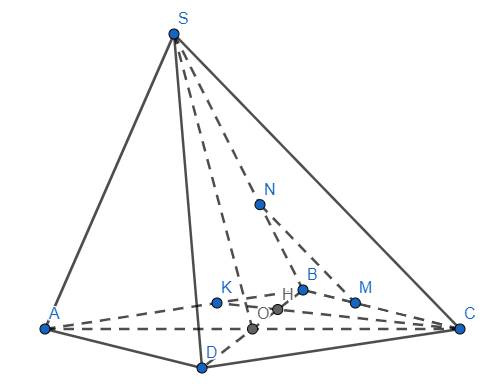
a) Ta có \(\left\{{}\begin{matrix}S\subset\left(SAC\right)\\S\subset\left(SBD\right)\end{matrix}\right.\)

và \(\left\{{}\begin{matrix}O\in AC\subset\left(SAC\right)\\O\in BD\subset\left(SBD\right)\end{matrix}\right.\) nên SO chính là giao tuyến của (SAC) và (SBD)

b) Trong mp(ABCD) cho CK cắt BD tại H. Do \(BD\subset\left(SBD\right)\) nên H cũng là giao điểm của CK và (SBD).

c) Vì \(\dfrac{BN}{NS}=\dfrac{BM}{MC}=\dfrac{1}{2}\) \(\Rightarrow\) MN//SC (Thelas đảo)

\(\Rightarrow\) MN//(SAC)

Rất rõ ràng là câu A nhé bạn, vì \(O\in AC\subset\left(SAC\right)\)

 Ở đây ta kí hiệu \(N,P,F_k,F_{ms}\) lần lượt là phản lực mặt sàn tác dụng lên thùng; trong lực của thùng; lực kéo, lực ma sát tác dụng lên vật. Chọn chiều (+) là chiều chuyển động của vật.

a) Do vật di chuyển theo phương ngang nên \(N=P=mg=50.10=500\left(N\right)\)

 Ta có \(F_{ms}=\mu N=0,4.500=200\left(N\right)\)

b) Áp dụng định luật II Newton, ta có \(\overrightarrow{F}=m\overrightarrow{a}\) 

Chiếu lên phương chuyển động của vật, ta có

\(F_k-F_{ms}=ma\) \(\Leftrightarrow a=\dfrac{F_k-F_{ms}}{m}=\dfrac{220-200}{50}=0,4\left(m/s^2\right)\)

c) Quãng đường thùng dịch chuyển: \(s=\dfrac{1}{2}at^2=\dfrac{1}{2}.0,4.10^2=20\left(m\right)\)

d) Vận tốc của vật sau khi di chuyển được 2 giây: \(v=at=0,4.2=0,8\left(m/s\right)\)

Cách 1: Dùng định lý Menelaus đảo:

Từ đề bài, ta có \(\dfrac{BD}{BC}=\dfrac{2}{3}\), \(\dfrac{MC}{MA}=\dfrac{3}{2}\), \(\dfrac{IA}{ID}=1\)

\(\Rightarrow\dfrac{BD}{BC}.\dfrac{MC}{MA}.\dfrac{IA}{ID}=1\)

Theo định lý Menelaus đảo, suy ra B, I, M thẳng hàng.

Cách 2: Dùng vector

 Ta có \(\overrightarrow{BI}=\dfrac{1}{2}\left(\overrightarrow{BA}+\overrightarrow{BD}\right)\)

\(=\dfrac{1}{2}\overrightarrow{BA}+\dfrac{1}{2}.\dfrac{2}{3}\overrightarrow{BC}\)

\(=\dfrac{1}{2}\overrightarrow{BA}+\dfrac{1}{3}\overrightarrow{BC}\) 

\(=\dfrac{1}{6}\left(3\overrightarrow{BA}+2\overrightarrow{BC}\right)\)

Lại có \(\overrightarrow{BM}=\dfrac{MC}{AC}\overrightarrow{BA}+\dfrac{MA}{AC}\overrightarrow{BC}\)

\(=\dfrac{3}{5}\overrightarrow{BA}+\dfrac{2}{5}\overrightarrow{BC}\)

\(=\dfrac{1}{5}\left(3\overrightarrow{BA}+2\overrightarrow{BC}\right)\)

\(=\dfrac{6}{5}.\dfrac{1}{6}\left(3\overrightarrow{BA}+2\overrightarrow{BC}\right)\)

\(=\dfrac{6}{5}\overrightarrow{BI}\)

Vậy \(\overrightarrow{BM}=\dfrac{6}{5}\overrightarrow{BI}\), suy ra B, I, M thẳng hàng. 

code cho C++ nhé

#include <bits/stdc++.h>
using namespace std;
string s;
int res = 0;
int main()
{
    cin >> s;
    for (int i = 0; i < (int)s.size(); ++i) res += ((int(s[i]) >= 97 && int(s[i]) <= 122) ? 2 : 3);
    return cout << res, 0;
}