Luu Quynh Anh
Giới thiệu về bản thân



































Từ đề bài ta có: Số thứ nhất chiếm 2 phần; Số thứ 2 chiếm 3 phần Vì số thứ 2 bằng 1/3 số thứ 3 => Số thứ 3 chiếm 9 phần.
Số phần số thứ 3 hơn số thứ nhất là :
( phần )
Giá trị của 1 phần là :
Số thứ nhất là :
Số thứ 2 là :
Số thứ 3 là :
- Số thứ nhất:
- Số thứ hai:
- Số thứ ba:
Họa sĩ Bùi Xuân Phái
Trong số các danh họa Việt Nam, họa sĩ Bùi Xuân Phái (1920-1988) nổi tiếng nhất về chủ đề tranh phố cổ Hà Nội. Ông say mê vẽ những bức tranh miêu tả lại phố cổ Hà Nội trong thế kỷ 20, đã tạo nên một dòng tranh về chủ đề này với tên gọi “Phố Phái”.
) Tầng 1: 280 quyển
b) Tầng 2: 240 quyển; Tầng 3: 180 quyển
Giải thích các bước giải:
a) Số sách ở tầng 1 là
700 x 40 : 100 = 280 (quyển)
b) Tổng số sách ở tầng 2 và tầng 3 là
700 – 280 = 420 (quyển)
Sau khi chuyển thì tổng số sách ở hai tầng đó vẫn không thay đổi.
Số sách ở tầng 3 sau khi chuyển là
420 : (2 + 5) x 2 = 120 (quyển)
Số sách ở tầng 3 lúc đầu là
120 x 2 = 240 (quyển)
Số sách ở tầng 2 lúc đầu là
420 – 240 = 180 (quyển)
Đáp số: a) Tầng 1: 280 quyển
b) Tầng 2: 240 quyển; Tầng 3: 180 quyển
a) Tầng 1: 280 quyển
b) Tầng 2: 240 quyển; Tầng 3: 180 quyển
Giải thích các bước giải:
a) Số sách ở tầng 1 là
700 x 40 : 100 = 280 (quyển)
b) Tổng số sách ở tầng 2 và tầng 3 là
700 – 280 = 420 (quyển)
Sau khi chuyển thì tổng số sách ở hai tầng đó vẫn không thay đổi.
Số sách ở tầng 3 sau khi chuyển là
420 : (2 + 5) x 2 = 120 (quyển)
Số sách ở tầng 3 lúc đầu là
120 x 2 = 240 (quyển)
Số sách ở tầng 2 lúc đầu là
420 – 240 = 180 (quyển)
Đáp số: a) Tầng 1: 280 quyển
b) Tầng 2: 240 quyển; Tầng 3: 180 quyển
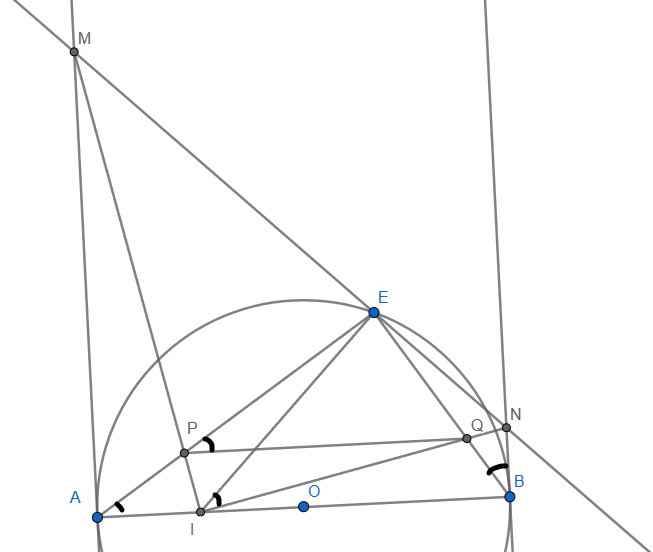 Mình gửi hình nhé
Mình gửi hình nhé



1. I usually ride a bike in spring.
2. You prepare dinner at 4 o'clock every day.
3. Mary and I go to school at quarter past 7.
4. my parents finish work at 4 o'clock in the afternoon.
Thể tích của bể hình hộp chữ nhật được tính bằng công thức \(V_{bể}=dài\cdot rộng\cdot cao\)
\(\Rightarrow V_{bể}=1,2\cdot0,8\cdot0,6=0,576m^3\)
Mực nước cao bằng 3 phần 4 chiều cao bề, tức là \(0,6\cdot\dfrac{3}{4}=0,45m\)
Ta có \(V_{nước}=V_{bể}-V_{sỏi}\)
Trước tiên, chuyển đổi thể tích của các viên sỏi từ dm³ sang m³: \(9,6dm^3=0,0096m^{^3}\)
\(\Rightarrow0,567-0,0096=0,5664\left(m^3\right)\)
Diện tích đáy bể = dài x rộng = 1,2x0,8=0,96m^2
Mực nước \(=\dfrac{V_{nước}}{S_{đáy}}=\dfrac{0,5664}{0,96}\)≈0.59m
Vậy mực nước trong bể lúc này cao khoảng 0.59 mét.
Gọi x là lưu lượng nước của vòi A trong một phút;
là lưu lượng nước của vòi B trong một phút.
Nếu mở cả hai vòi A và B cùng lúc, thì sau 30 phút bể đầy:
\(30\cdot\left(x+y\right)=1\left(bể\right)\)
\(\Rightarrow x+y=\dfrac{1}{30}\Rightarrow y=\dfrac{1}{30}-x\) (1)
Nếu mở vòi A trong 12 phút rồi đóng lại và mở vòi B trong 42 phút thì bể đầy: \(12x+42y=1\left(bể\right)\) (2)
Thay (1) vào (2) ta được:
\(12x+42\left(\dfrac{1}{30}-x\right)=1\)
\(\Rightarrow12x+42\cdot\dfrac{1}{30}-42x=1\)
\(\Rightarrow12x+1.4-42x=1\)
\(\Rightarrow-20x+4=1\)
\(\Rightarrow-30x=-0,4\)
\(\Rightarrow x=\dfrac{0,4}{30}=\dfrac{2}{150}=\dfrac{1}{75}\)
Thay giá trị của x vào phương trình ta được
\(\Rightarrow y=\dfrac{1}{30}-\dfrac{1}{75}=\dfrac{1}{50}\)
Vậy trong 1 phút bể A chảy được 1/75 bể và vòi chảy được 1/50 bể.
Gọi là thời gian mở vòi A trước khi mở vòi B. Để khi bể đầy, lượng nước chảy ra từ hai vòi bằng nhau:
\(t\cdot x=\left(30-t\right)\cdot y\)
\(\dfrac{1}{75}\cdot t=\left(30-t\right)\cdot\dfrac{1}{50}\)
\(\Rightarrow50t=75\left(30-t\right)\)
\(\Rightarrow50t=2250-75t\)
\(\Rightarrow125t=2250\)
\(\Rightarrow t=\dfrac{2250}{125}=18\)
Vậy cần mở vòi A trước 18 phút để khi bể đầy để lượng nước chảy ra từ hai vòi bằng nhau.