a) Δ��� Tam giác ABC vuông cân nên góc B= góc C = 45 độ

Tam giácBHE vuông tại H có góc BEH + góc B = 90 độ

Suy ra góc BEH = 90 độ - 45 độ = 45 độ nên góc B= góc BEH = 45 độ

Vậy tam giác BEH vuông tại H

b) Chứng minh tương tự như câu a ta được tam giác CFG vuông tại G nên GF=GC và HB=HE

Lại có BH=HG=GC suy ra EH=HG=GF và EH//FG ( cùng vuông góc với BC)

Tứ giác EFGH có EH//FG, EH=FG

=>tứ giác EFGH là hình bình hành 

Xét hình bình hành có một góc vuông là góc H nên là hình chữ nhật

Mà hình chữ nhật có hai cạnh kề bằng nhau là EH=HG nên là hình vuông

Vậy EFGH là hình vuông

AC⊥Oy (gt); \(O x \bot O y\) (gt) => AC//Oy => AC//OB

C/m tương tự có AB//OC

=> OBAC là hình bình hành (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh)

Mà \(\hat{x O y} = 9 0^{o}\)

=> OBAC là HCN

Ta có

AC=AB (Tính chất đường phân giác)

=> OBAC là hình vuông

a)ABCD là hình bình hành nên hai đường chéo AC,BD cắt nhau tại O là trung điểm của mỗi đường.

Xét ΔOBM và ΔODP có:

     OB=OD ( giả thiết)

     GOC OBM=ODP (so le trong)

     BOM=DOP (đối đỉnh)

Vậy ΔOBM=ΔODP (g.c.g)

Suy ra,OM=OP (hai cạnh tương ứng)

Chứng minh tương tự ΔOAQ=ΔOCN (g.c.g) suy ra OQ=ON (hai cạnh tương ứng)

MNPQ có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên là hình bình hành.

b) Hình bình hành ����MNPQ có hai đường chéo ��⊥��MP⊥NQ nên là hình thoi.

a) ABCD là hình bình hành nên AB=DC suy ra AB=​DC

Do đó AM=BM=DN=CN.

Tứ giác AMCN có AM // NC,AM=NC nên là hình bình hành.

Lại có ΔADC vuông tại A có AN là đường trung tuyến nên AN=​DC=DN=CN.

Hình bình hành AMCN có hai cạnh kề bằng nhau nên là hình thoi, khi đó hai đường chéo AC,MN vuông góc với nhau.

Tứ giác AMCN là hình thoi.

Ta có ABCD là hình thoi nên AC⊥BD tại trung điểm của mỗi đường nên BD là trung trực của AC

Suy ra GA=GC,HA=HC (1)(1)

Và AC là trung trực của BD suy ra AG=AH,CG=CH (2)(2)

Từ (1),(2)(1),(2) suy ra AG=GC=CH=HA nên AGCH là hình thoi.

a) Ta có:Ax⊥AC và By // AC

=> Ax⊥By
⇒Góc AMB = 90 độ

Xét ΔMAQ và ΔQBM có

Góc MQA = góc BQM (so le trong);

MQ là cạnh chung;

Góc AMQ = góc BQM(Ax//QB)

Suy ra ,ΔMAQ= ΔQBM (g-c-g)

Suy ra góc MBQ = góc MAQ= 90 độ (2 góc tương ứng)

Xét tứ giác AMBQ có

Góc QAM = góc AMB = góc MBQ = 90 độ

=> tứ giácAMBQ là hình chữ nhật.

b) Do tứ giác AMBQ là hình chữ nhật

Mà P là trung điểm AB

=>P là trung điểm của MQ; AB = MQ

=> PQ = 1/2 AB (1) 

Xét  tam giác AIB vuông tại I và có IP là đường trung tuyến

=> IP = 1/2 AB(2)

Từ (1) và (2)

=> QP =IP 

=> Tam giác PQI cân tại P

• Vì \(\angle A = \angle D = 90^{\circ}\) nên \(A B \parallel D C\) và \(A B \bot A D\), \(D C \bot A D\).
• \(M\) là trung điểm \(A C\) nên \(A M = M C = \frac{1}{2} A C\).
• \(B M = \frac{1}{2} A C\) (theo giả thiết).
• Do đó, \(A B C D\) có 4 góc vuông (vì tổng góc tứ giác là \(360^{\circ}\) và hai góc ở \(A , D\) đã vuông).
• Vậy \(A B C D\) là hình chữ nhật.

Xét tứ giác AHCD có 

I là trung điểm của đường chéo AC

I là trung điểm của đường chéo HD

Do đó: AHCD là hình bình hành

mà \(\hat{A H C} = 9 0^{0}\)

nên AHCD là hình chữ nhật

a) Do ABCD là hình bình hành

\(\Rightarrow A D = B C\) và \(A D\) // \(B C\)

Do \(A D\) // \(B C\) (cmt)

\(\Rightarrow \hat{A D H} = \hat{C B K}\) (so le trong)

Xét hai tam giác vuông: \(\Delta A D H\) và \(\Delta C B K\) có:

\(A D = B C\) (cmt)

\(\hat{A D H} = \hat{C B K}\) (cmt)

\(\Rightarrow \Delta A D H = \Delta C B K\) (cạnh huyền - góc nhọn)

\(\Rightarrow A H = C K\) (hai cạnh tương ứng)

Do \(A H \bot B D\) (gt)

\(C K \bot B D\) (gt)

\(\Rightarrow A H\) // \(C K\)

Xét tứ giác AHCK có:

\(A H\) // \(C K\) (cmt)

\(A H = C K\) (cmt)

\(\Rightarrow A H C K\) là hình bình hành

b) Do AHCK là hình bình hành (cmt)

\(I\) là trung điểm của HK (gt)

\(\Rightarrow I\) là trung điểm của AC

Do ABCD là hình bình hành (gt)

\(I\) là trung điểm của AC (cmt)

\(\Rightarrow I\) là trung điểm của BD

\(\Rightarrow I B = I D\)

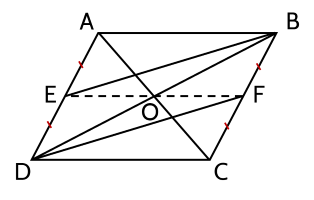a) Ta có : t/g ABCD là hbh 

Suy ra : AD=BC

Mà E là trung điểm của AD ; F là trung điểm của BC

Suy ra : AE=DE=BF=CF

Xét tứ giác EBFD có : BF//ED ( BC//AD )

                                    BF=ED ( cmt )

Suy ra : t/g EBFD là hbh.

b) Từ O là giao điểm của hai đường chéo của hbh ABCD hay là giao điểm của AC và BD.

Suy ra : O là trung điểm của BD hay 3 điểm B ; O ; D thẳng hàng 

Ta có : t/g EBFD là hbh ( cmt ) 

Suy ra : BD cắt EF tại trung điểm của mỗi đường .

Mà O là trung điểm của BD 

Suy ra : O cũng là trung điểm của EF.

suy ra : 3 điểm F;O;E thẳng hàng.