x2+xy+2023x+2022y+2023=0

\(x^{2} + x y + x + 2022 x + 2022 y + 2022 + 1 = 0\)

\(x \left(\right. x + y + 1 \left.\right) + 2022 \left(\right. x + y + 1 \left.\right) = - 1\)

\(\left(\right. x + 2022 \left.\right) \left(\right. x + y + 1 \left.\right) = - 1\)

\(x + 2022 = 1\) hoặc \(x + y + 1 = - 1\)

\(x + 2022 = - 1\) hoặc \(x + y + 1 = 1\)

\(x = - 2021\) và \(y = 2019\) hoặc \(x = - 2023\) và \(y = 2023\)

Vậy \(\left(\right. x ; y \left.\right) \in \left{\right. \left(\right. - 2021 ; 2019 \left.\right) ; \left(\right. - 2023 ; 2023 \left.\right) \left.\right}\).

Từ \(x + y + z = 0\) suy ra \(x + y = - z\)

\(x^{2} + 2 x y + y^{2} = z^{2}\)

\(x^{2} + y^{2} - z^{2} = - 2 x y\).

Tương tự ta có: \(y^{2} + z^{2} - x^{2} = - 2 y z\) và \(z^{2} + x^{2} - y^{2} = - 2 z x\).

Do đó \(A = \frac{x y}{- 2 x y} + \frac{y z}{- 2 y z} + \frac{z x}{- 2 z x} = - \frac{1}{2} - \frac{1}{2} - \frac{1}{2} = - \frac{3}{2}\).

Vậy \(A = - \frac{3}{2}\).

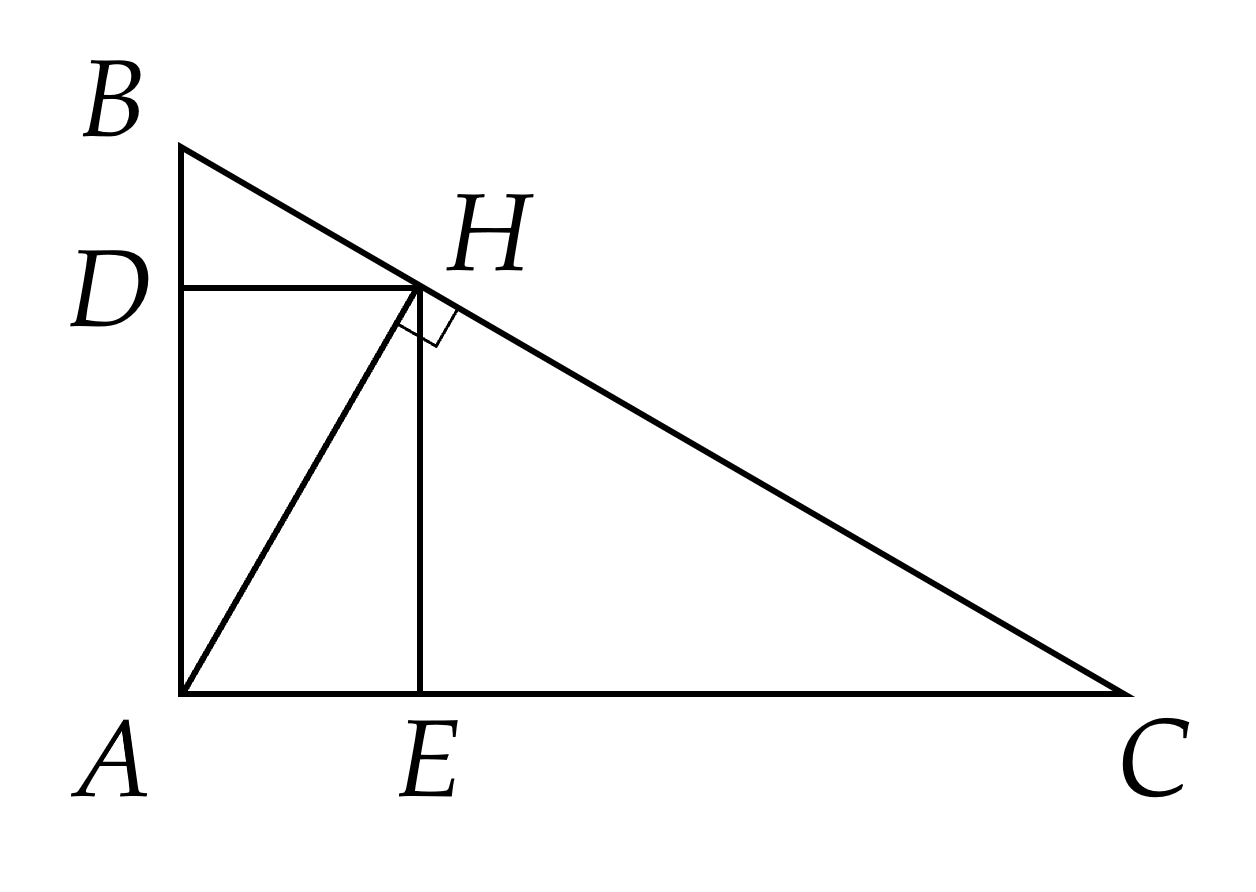
a) \(\Delta A B C\) vuông tại \(A\) suy ra \(\hat{B A C} = 9 0^{\circ}\) suy ra \(\hat{D A E} = 9 0^{\circ}\).

Do \(H D ⊥ A B\) suy ra \(\hat{H D A} = 9 0^{\circ}\); \(H E ⊥ A C\) suy ra \(\hat{H E A} = 9 0^{\circ}\).

Tứ giác \(A D H E\) có \(\hat{D A E} = \hat{H D A} = \hat{H E A} = 9 0^{\circ}\) suy ra tứ giác \(A D H E\) là hình chữ nhật. 

b) Do \(\Delta A H D\) vuông tại \(D\), áp dụng định lí Pythagore suy ra:

\(A H^{2} = A D^{2} + D H^{2}\)

\(25 = 16 + D H^{2}\)

\(D H^{2} = 9\) nên \(D H = 3\) cm.

Do \(A D H E\) là hình chữ nhật suy ra \(S_{A D H E} = A D . D H = 4.3 = 12\) (cm\(^{2}\)).

Vì đồ thị hàm số \(y = a x + b\) đi qua điểm \(A \left(\right. - 1 ; 2 \left.\right)\) nên ta có:

   \(2 = - 1. a + b\) suy ra \(- a + b = 2\)

Vi đồ thị hàm số \(y = a x + b\) đi qua điểm \(B \left(\right. 1 ; 4 \left.\right)\) nên ta có:

   \(4 = 1. a + b\) suy ra \(a + b = 4 \left(\right. 2 \left.\right)\)

Từ (1) và (2) ta tìm được \(a = 1 ; b = 3\)

Vậy hàm số cần tìm là \(y = x + 3\).

a) Thay \(x = 2\) (thỏa mãn điều kiện xác định) vào \(Q = \frac{x + 1}{x^{2} - 9}\), ta được:

\(Q = \frac{x + 1}{x^{2} - 9} = \frac{2 + 1}{2^{2} - 9} = \frac{3}{- 5} = - \frac{3}{5}\).

b) \(P = \frac{2 x^{2} - 1}{x \left(\right. x + 1 \left.\right)} - \frac{\left(\right. x - 1 \left.\right) \left(\right. x + 1 \left.\right)}{x \left(\right. x + 1 \left.\right)} + \frac{3 x}{x \left(\right. x + 1 \left.\right)}\)

\(P = \frac{2 x^{2} - 1 - \left(\right. x^{2} - 1 \left.\right) + 3 x}{x \left(\right. x + 1 \left.\right)}\)

\(P = \frac{2 x^{2} - 1 - x^{2} + 1 + 3 x}{x \left(\right. x + 1 \left.\right)}\)

\(P = \frac{x^{2} + 3 x}{x \left(\right. x + 1 \left.\right)} = \frac{x + 3}{x + 1}\).

c) Ta có \(M = P . Q = \frac{x + 3}{x + 1} . \frac{x + 1}{x^{2} - 9} = \frac{x + 3}{\left(\right. x - 3 \left.\right) \left(\right. x + 3 \left.\right)} = \frac{1}{x - 3}\)

\(M = \frac{- 1}{2}\) suy ra \(\frac{1}{x - 3} = \frac{- 1}{2}\)

\(x - 3 = - 2\)

\(x = 1\).

Vậy với \(x = 1\) thì\(M = \frac{- 1}{2}\).

a) \(5 \left(\right. x + 2 y \left.\right) - 15 x \left(\right. x + 2 y \left.\right) = 5 \left(\right. x + 2 y \left.\right) . \left(\right. 1 - 3 x \left.\right)\).

b) \(4 x^{2} - 12 x + 9 = \left[\right. \left(\left(\right. 2 x \left.\right)\right)^{2} - 2.2 x . 3 + 3^{2} \left]\right. = \left(\left(\right. 2 x - 3 \left.\right)\right)^{2}\).

c) \(\left(\left(\right. 3 x - 2 \left.\right)\right)^{3} - 3 \left(\right. x - 4 \left.\right) \left(\right. x + 4 \left.\right) + \left(\left(\right. x - 3 \left.\right)\right)^{3} - \left(\right. x + 1 \left.\right) \left(\right. x^{2} - x + 1 \left.\right)\)

\(= 27 x^{3} - 54 x^{2} + 36 x - 8 - 3 \left(\right. x^{2} - 16 \left.\right) + x^{3} - 9 x^{2} + 27 x - 27 - \left(\right. x^{3} + 1 \left.\right)\)

\(= \left(\right. 27 x^{3} + x^{3} - x^{3} \left.\right) + \left(\right. - 54 x^{2} - 3 x^{2} - 9 x^{2} \left.\right) + \left(\right. 36 x + 27 x \left.\right) + \left(\right. - 8 + 48 - 27 - 1 \left.\right)\)

\(= 27 x^{3} - 66 x^{2} + 63 x + 12\).

​\(A = 5 + 2 x y + 14 y - x^{2} - 5 y^{2} - 2 x\)

\(= - \left(\right. x^{2} + y^{2} + 1 - 2 x y - 2 y + 2 x \left.\right) - \left(\right. 4 y^{2} - 12 y + 9 \left.\right) + 15\)

\(= - \left(\left(\right. x - y + 1 \left.\right)\right)^{2} - \left(\left(\right. 2 y - 3 \left.\right)\right)^{2} + 15 \leq 15\)

Suy ra giá trị lớn nhất của \(A = 15\) khi và chỉ khi:

\(x - y = - 1\) và \(2 y - 3 = 0\)

Suy ra \(x = \frac{1}{2}\) và \(y = \frac{3}{2}\).

a) Góc ngoài tại đỉnh \(B\) có số đo bằng \(7 0^{\circ}\) nên góc trong tại đỉnh \(B\) có số đo bằng \(18 0^{\circ} - 7 0^{\circ} = 11 0^{\circ}\)

Xét tứ giác \(A B C D ,\) ta có: \(\hat{A} + \hat{B} + \hat{C} + \hat{D} = 36 0^{\circ}\)

Do đó \(3 x + 11 0^{\circ} + x + 9 0^{\circ} = 36 0^{\circ}\)

uy ra \(4 x = 16 0^{\circ}\) nên \(x = 4 0^{\circ}\)

Vậy \(x = 4 0^{\circ}\).

b) Áp dụng định lí Pythagore vào tam giác \(A B H\) vuông tại \(H\) ta có: \(A B^{2} = A H^{2} + B H^{2}\)

Suy ra \(A H^{2} = A B^{2} - B H^{2}\)

Do đó \(A H = \sqrt{A B^{2} - B H^{2}} = \sqrt{3 , 7^{2} - 1 , 2^{2}} = 3 , 5\) m

Ta có \(\frac{A H}{B H} = \frac{3 , 5}{1 , 2} \approx 2 , 9\)

Mà \(2 , 9 > 2 , 2\) nên khoảng cách đặt thang cách chân tường đã cho là không an toàn.

Thể tích khúc gỗ hình lập phương là: \(30^{3} = 27 000\) (cm³).

Thể tích của phần gỗ còn lại hình chóp tứ giác đều là: \(\frac{1}{3} \left(. 30\right)^{2} . 30 = 9 000\) (cm³).

Thể tích của khối gỗ bị cắt đi là: \(27 000 - 9 000 = 18 000\) (cm³).

a) \(x^{2} - 2 x + 1 - y^{2}\)

\(= \left(\right. x^{2} - 2 x + 1 \left.\right) - y^{2}\)

\(= \left(\left(\right. x - 1 \left.\right)\right)^{2} - y^{2}\)

\(= \left(\right. x - 1 - y \left.\right) \left(\right. x - 1 + y \left.\right) .\)

b) \(x^{2} - 8 x + 12\)

\(= x^{2} - 2 x - 6 x + 12\)

\(= \left(\right. x^{2} - 2 x \left.\right) - \left(\right. 6 x - 12 \left.\right)\)

\(= x \left(\right. x - 2 \left.\right) - 6 \left(\right. x - 2 \left.\right)\)

\(= \left(\right. x - 2 \left.\right) \left(\right. x - 6 \left.\right) .\)