Chia \(2012\) số \(1\); \(\sqrt{2}\); \(\sqrt{3}\); ... ; \(\sqrt{2024}\) thành \(44\) đoạn gồm \(\left[\right. \sqrt{1} ; \sqrt{3} \left]\right.\); \(\left[\right. \sqrt{4} ; \sqrt{8} \left]\right.\); ...; \(\left[\right. \sqrt{1936} ; \sqrt{2012} \left]\right.\).

 Các đoạn trên có dạng tổng quát là \(\left[\right. \sqrt{k^{2}} ; \sqrt{\left(\right. k + 1 \left.\right)^{2} - 1} \left]\right.\) với \(k \geq 1\).

Như vậy \(90\) số thuộc tập hợp \(X\) nằm trong \(44\) đoạn trên. Theo nguyên lí Dirichlet thì tồn tại ba số trong \(90\) số trên nằm trong cùng một đoạn.

Không mất tính tổng quát, ta giả sử hai số đó là \(x\), \(y\), \(z\) và chúng nằm trong đoạn \(\left[\right. \sqrt{k^{2}} ; \sqrt{\left(\right. k + 1 \left.\right)^{2} - 1} \left]\right.\).

Chia đoạn \(\left[\right. \sqrt{k^{2}} ; \sqrt{\left(\right. k + 1 \left.\right)^{2} - 1} \left]\right.\) thành hai đoạn \(\left[\right. \sqrt{k^{2}} ; \sqrt{\left(\right. k^{2} + k} \left]\right.\) và \(\left[\right. \sqrt{k^{2} + k} ; \sqrt{\left(\right. k + 1 \left.\right)^{2} - 1} \left]\right.\). Khi đó theo nguyên lí Dirichlet tồn tại hai số nằm trên cùng một đoạn. Giả sử hai số đó là \(x\), \(y\). Khi đó:

 Nếu \(x\) và \(y\) nằm trên đoạn \(\left[\right. \sqrt{k^{2}} ; \sqrt{\left(\right. k^{2} + k} \left]\right.\) thì ta được

\(\mid x - y \mid \leq \sqrt{k^{2} + k} - \sqrt{k^{2}} < \sqrt{k^{2} + k + \frac{1}{4}} - \sqrt{k^{2}} = k + \frac{1}{2} - k = \frac{1}{2} .\)

 Nếu \(x\) và \(y\) nằm trên đoạn \(\left[\right. \sqrt{k^{2} + k} ; \sqrt{\left(\right. k + 1 \left.\right)^{2} - 1} \left]\right.\) thì ta được:

\(\mid x - y \mid \leq \sqrt{\left(\right. k + 1 \left.\right)^{2} - 1} - \sqrt{k^{2} + k} = \frac{\left(\right. k + 1 \left.\right)^{2} - 1 - k^{2} - k}{\sqrt{\left(\right. k + 1 \left.\right)^{2} - 1} + \sqrt{k^{2} + k}} \&\text{nbsp}; < \frac{k}{2 k} \&\text{nbsp}; = \frac{1}{2} .\)

Vậy trong \(90\) số khác nhau bất kì được lấy ra từ tập \(X\) luôn tồn tại hai số \(x\), \(y\) sao cho \(\mid x - y \mid < \frac{1}{2}\).

Biến đổi phương trình trở thành:

\(\left(\left(\right. a^{2} + a b + b^{2} - 3 \left.\right)\right)^{2} + 3 \left(\right. a - b \left.\right)^{2} = 0\)

\(a^{2} + a b + b^{2} = 3\) và \(\left(\right. a - b \left.\right)^{2} = 0\)

\(a^{2} + a b + b^{2} = 3\) và \(a = b\).

Thay \(a = b\) vào \(a^{2} + a b + b^{2} = 3\), ta được:

\(a^{2} + a . a + a^{2} = 3\)

\(a^{2} = 1\)

Hay \(a = b = 1\) hoặc \(a = b = - 1\).

Vậy ta tìm được hai cặp \(\left(\right. a ; b \left.\right)\) là \(\left(\right. 1 ; 1 \left.\right)\) và \(\left(\right. - 1 ; - 1 \left.\right)\).

1) Diện đáy của hình chóp tứ giác đều là

\(6 250.3 : 30 = 625\) (cm\(^{2}\))

Độ dài cạnh đáy của hình chóp tứ giác đều là

\(\sqrt{625} = 25\) (cm)

2) 

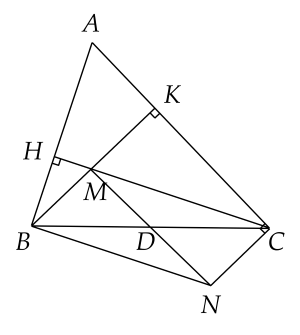
a) Xét tứ giác \(B M C N\) có hai đường chéo \(M N\) và \(B C\) cắt nhau tại trung điểm mỗi đường, đo đó \(B M N C\) là hình bình hành.

b) Vì \(B M C N\) là hình bình hành nên ta suy ra \(B M / / N C\). Vậy \(B K C N\) là hình thang. Mặt khác do \(\hat{B K C} = 9 0^{\circ}\) nên \(B M C N\) là hình thang cân.

c) Để \(B M C N\) là hình thoi thì \(M D \bot B C\).

Mặt khác ta cũng có \(A M \bot B C\) (giao điểm ba đường cao).

Kẻ đường thẳng \(d\) vuông góc với \(B C\), từ đây ta suy ra

\(M D / / d\) và \(A M / / d\). Vậy theo tiên đề Euclid, ta có 3 điểm \(M , A , D\) thẳng hàng, hay \(A D\) vừa là đường cao và vừa là đường trung tuyến của tam giác \(A B C\).

Dễ dàng chứng minh được \(\Delta A M D = \Delta A D C\), từ đó suy ra \(A B = A C\), hay tam giác \(A B C\) cân tại \(A\).

Vậy để \(B M C N\) là hình thoi thì \(\Delta A B C\) là tam giác cân.

Gọi phương trình đường thẳng \(A B\) là \(y = a x + b\) \(\left(\right. a , b \in \mathbb{R}\) và \(a \neq 0 \left.\right)\).

Ta có \(A \left(\right. - 3 ; 0 \left.\right) \in A B\) suy ra \(0 = a . \left(\right. - 3 \left.\right) + b\) hay \(b = 3 a\).

\(B \left(\right. 0 ; 2 \left.\right) \in A B\) suy ra \(2 = a . 0 + b\) hay \(b = 2\). Từ đó suy ra \(a = \frac{2}{3}\).

Vậy phương trình đường thẳng \(A B\) là \(y = \frac{2}{3} x + 2\).

a) Điều kiện: \(x \neq 0 , x \neq - 5\).

b) \(A = \frac{x^{2} + 2 x}{2 x + 10} + \frac{x - 5}{x} - \frac{5 x - 50}{2 x \left(\right. x + 5 \left.\right)}\)

\(= \frac{x^{2} + 2 x}{2 x + 10} + \frac{x - 5}{x} + \frac{50 - 5 x}{2 x \left(\right. x + 5 \left.\right)}\)

\(= \frac{x^{3} + 2 x^{2} + 2 x^{2} - 50 + 50 - 5 x}{2 x \left(\right. x + 5 \left.\right)}\)

\(= \frac{x \left(\right. x^{2} + 2 x + 2 x - 5 \left.\right)}{2 x \left(\right. x + 5 \left.\right)}\)

\(= \frac{x^{2} - x + 5 x - 5}{2 \left(\right. x + 5 \left.\right)}\)

\(= \frac{\left(\right. x - 1 \left.\right) \left(\right. x + 5 \left.\right)}{2 \left(\right. x + 5 \left.\right)} = \frac{x - 1}{2}\)

Nếu giá trị của biểu thức bằng \(1\) thì giá trị của \(\frac{x - 1}{2}\) cũng bằng \(1\). Ta có : \(\frac{x - 1}{2} = 1\) khi \(x - 1 = 2\) hay \(x = 3\). 

Vì \(x = 3\) thoả mãn điều kiện nên đó là giá trị phải tìm.

c) Tương tự \(\frac{x - 1}{2} = - \frac{1}{2}\) khi \(x - 1 = - 1\) hay \(x = 0\) (không thoả mãn điều kiện). Vậy không có giá trị nào của \(x\) để phân thức có giá trị bằng \(- \frac{1}{2}\).

d) Tương tự \(\frac{x - 1}{2} = - 3\) khi \(x - 1 = - 6\) hay \(x = - 5\) (không thoả mãn điểu kiện). Vậy không có giá trị nào của \(x\) để phân thức có giá trị bằng \(- 3.\)

Phân tích đa thức sau thành nhân tử:

a) \(2 x \left(\right. x - 3 y \left.\right) - 25 \left(\right. 3 y - x \left.\right)\)

\(= 2 x \left(\right. x - 3 y \left.\right) + \&\text{nbsp}; 25 \left(\right. x - 3 y \left.\right)\)

\(= \left(\right. 2 x + \&\text{nbsp}; 25 \left.\right) \left(\right. x - 3 y \left.\right)\)

b) \(36 x^{2} - 24 x + 4\);

\(= \left(\right. 6 x \left.\right)^{2} - 2.6 x . 2 + 2^{2}\)

\(= \left(\right. 6 x - 2 \left.\right)^{2}\)

c) \(\left(\right. 3 x + 2 \left.\right)^{2} + 2. \left(\right. 3 x + 2 \left.\right) . \left(\right. 3 x - 1 \left.\right) + \left(\right. 3 x - 1 \left.\right)^{2}\).

\(= \left(\right. 3 x + 2 + 3 x - 1 \left.\right)^{2}\)

\(= \left(\right. 6 x + 1 \left.\right)^{2}\)

a) \(\left(\right. 6 x^{3} y^{2} - 27 x^{3} y \left.\right) : 3 x y = 2 x^{2} y - 9 x^{2}\).

b) \(\left(\right. \frac{2}{3^{2}} x^{4} \left.\right) . \left(\right. 3 y x^{5} \left.\right) = \left(\right. \frac{2}{9} . 3 \left.\right) \left(\right. x^{4} \cdot x^{5} \left.\right) y = \frac{2}{3} x^{9} y\).

c) \(\frac{x^{2}}{x^{2} - 4} + \frac{1}{x - 2} + \frac{1}{x + 2} = \frac{x^{2}}{\left(\right. x - 2 \left.\right) \left(\right. x + 2 \left.\right)} + \frac{x + 2}{\left(\right. x - 2 \left.\right) \left(\right. x + 2 \left.\right)} + \frac{x - 2}{\left(\right. x - 2 \left.\right) \left(\right. x + 2 \left.\right)} = \frac{x^{2} + x + 2 + x - 2}{\left(\right. x - 2 \left.\right) \left(\right. x + 2 \left.\right)} = \frac{x^{2} + 2 x}{\left(\right. x - 2 \left.\right) \left(\right. x + 2 \left.\right)} = \frac{x \left(\right. x + 2 \left.\right)}{\left(\right. x - 2 \left.\right) \left(\right. x + 2 \left.\right)} = \frac{x}{x - 2}\).

d) \(\frac{2}{x - y} - \left(\right. \frac{x}{x - 1} - \frac{2}{y - x} \left.\right) - \left(\right. \frac{- 2}{x + y} - \frac{x}{x - 1} \left.\right) = \frac{2}{x - y} - \frac{x}{x - 1} + \frac{2}{y - x} + \frac{2}{x + y} + \frac{x}{x - 1} = \left(\right. \frac{2}{x - y} + \frac{2}{y - x} \left.\right) + \left(\right. - \frac{x}{x - 1} + \frac{x}{x - 1} \left.\right) + \frac{2}{x + y} = \frac{2}{x + y}\).

a) \(x^{2} - 3 x = 0\)

\(x^{2} - 3 x = 0\) suy ra \(x \left(\right. x - 3 \left.\right) = 0\)

TH1: \(x = 0\)

TH2: \(x - 3 = 0\) hay \(x = 3\).

b) \(x^{2} - 6 x + 8 = 0\)

\(x^{2} - 6 x + 8 = 0\)

\(\left(\right. x^{2} - 4 x \left.\right) - \left(\right. 2 x - 8 \left.\right) = 0\)

\(\left(\right. x - 4 \left.\right) \left(\right. x - 2 \left.\right) = 0\)

TH1: \(x - 4 = 0\) suy ra \(x = 4\)

TH2: \(x - 2 = 0\) suy ra \(x = 2\)

Vậy \(x = 4\) hoặc \(x = 2\).

1. Đổi: \(100\) cm \(= 10\) dm.

Thể tích của hình chóp tứ giác đều đó là:

   \(V = \frac{1}{3} . S_{đ} \&\text{nbsp}; . h = \frac{1}{3} . 30.10 = 100\) (dm\(^{3}\)) 

2. Xét phương trình hoành độ giao điểm của \(d_{1}\) và \(d_{2}\):

\(x + 4 = - x + 4\) suy ra \(2 x = 0\) nên \(\&\text{nbsp}; x = 0\).

Thay \(x = 0\) vào một trong hai hàm số của \(d_{1}\) và \(d_{2}\) ta tìm được \(y = 4\).

Vậy tọa độ giao điểm của hai đường thẳng thẳng \(d_{1}\) và \(d_{2}\) là \(\left(\right. 0 ; 4 \left.\right)\).

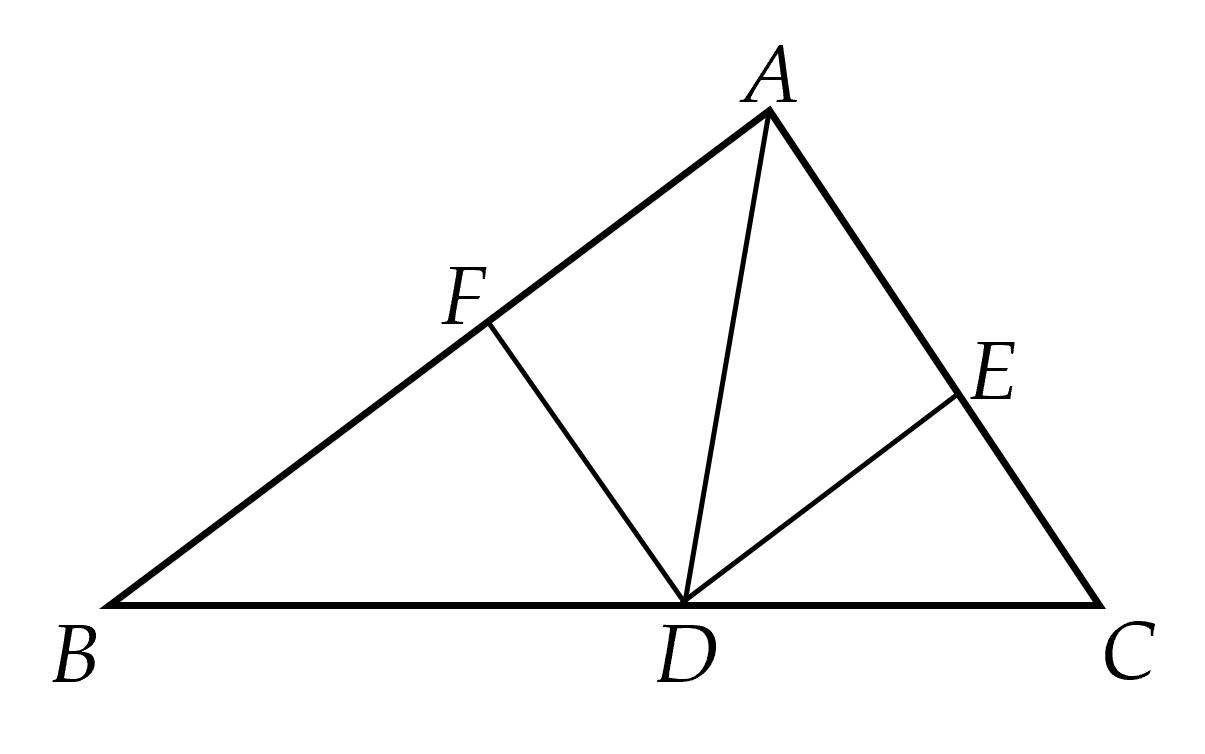
a) Xét tứ giác \(A E D F\) có:

\(D E\) // \(A F\) (do \(D E\) // \(A B\));

\(D F\) // \(A E\) (do \(D F\) // \(A C \left.\right)\).

Suy ra \(A E D F\) là hình bình hành (DHNB)

Mà đường chéo \(A D\) là tia phân giác của \(\hat{F A E}\) (gt)

Nên \(A E D F\) là hình thoi (DHNB).

b) Vì \(A E D F\) là hình thoi (cmt) nên \(D E\) // \(A F\); \(D E = A F\) (tính chất)

Mà \(A F = G F\) (gt) ; \(G\) thuộc tia đối của tia \(F A\) (gt) nên \(D E = G F\); \(D E\) // \(D F\) 

Xét tứ giác \(E F G D\) có: \(D E = G F\) (cmt); \(D E\) // \(G F\) (cmt)

Vậy \(E F G D\) là hình bình hành.

c) Theo bài ra, \(G\) thuộc tia đối của tia \(F A\) và \(F A = F G\) suy ra \(F\) là trung điểm của \(A G\)

Ta có: \(A G = 2 A F\); \(I D = 2 D F\)

Mà \(A F = D F\) (do \(A E D F\) là hình thoi) suy ra \(A G = I D\)

Xét tứ giác \(A D G I\) có:

Hai đường chéo \(A G\) và \(I D\) cắt nhau tại trung điểm \(F\) của mỗi đường;

Suy ra \(A D G I\) là hình bình hành (DHNB)

Lại có \(A G = I D\) (cmt) suy ra \(A D G I\) là hình chữ nhật (DHNB)

\(G D\) // \(I A\) suy ra \(G D\) // \(A K\) (\(A , I , K\) thẳng hàng)

Xét tứ giác \(A K D G\) có: \(G D\) // \(A K\) (cmt) ; \(D K\) // \(A G \left(\right.\) do \(D E\) // \(A F \left.\right)\) 

Suy ra \(A K D G\) là hình bình hành (DHNB) 

Khi đó hai đường chéo \(A D\) và \(G K\) cắt nhau tại trung điểm của mỗi đường 

Mà \(O\) là trung điểm của \(A D\) (do \(O\) là giao điểm của hai đường chéo trong hình thoi \(A E D F \left.\right)\) 

Vậy \(O\) là trung điểm của \(G K\).