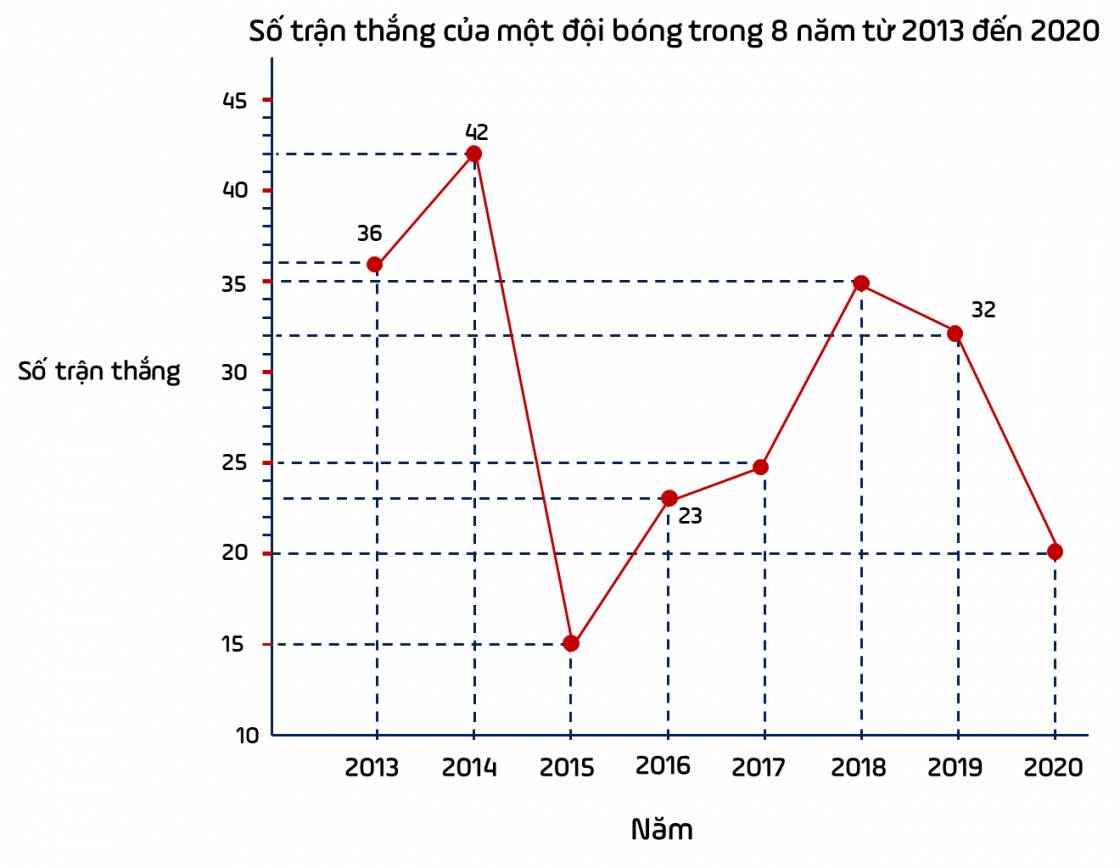
- Nhận xét: Từ năm 2015 đến năm 2018, số trận thắng của đội bóng có xu hướng tăng.

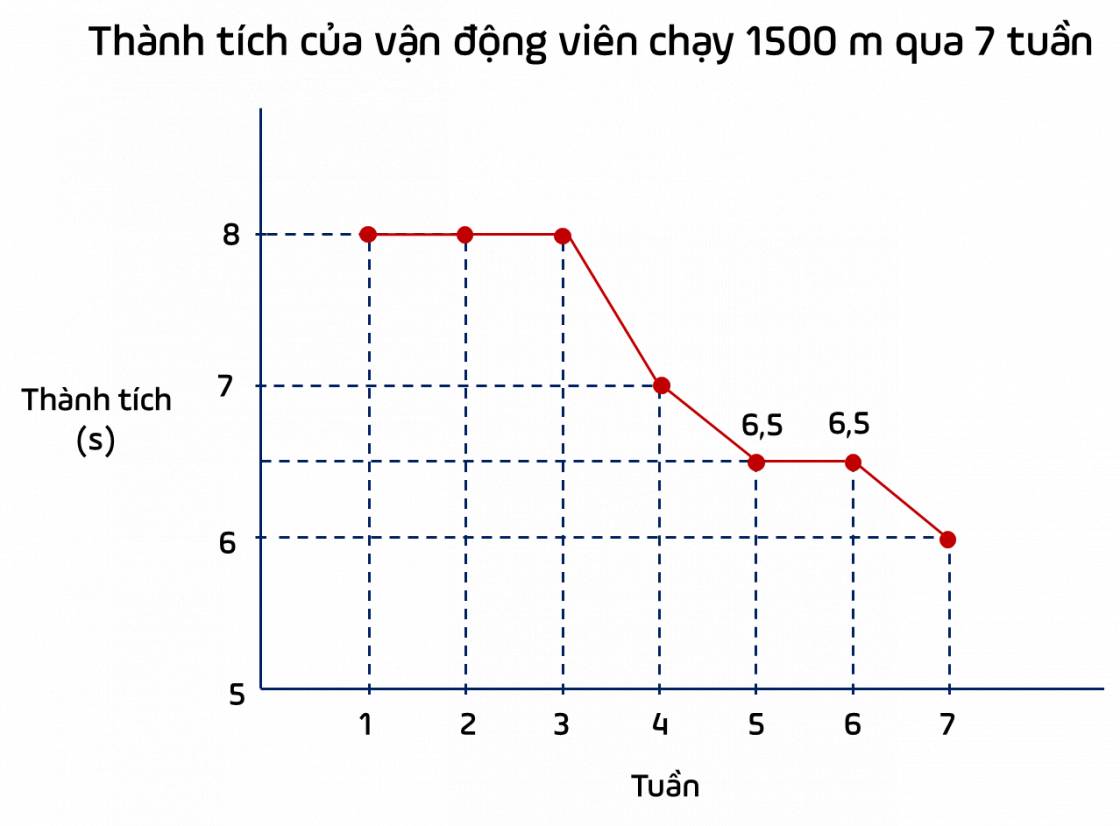
Nhận xét: Từ tuần 1 đến tuần 3, biểu đồ nằm ngang, nên trong thời gian này, thành tích của cận động viên giữ nguyên là 8 phút.

Từ tuần 3 đến tuần 5, biểu đồ có xu hướng đi xuống, nên trong thời gian này, thành tích của cận động viên đã được cải thiện từ 8 phút xuống đến 6,5 phút (chạy nhanh hơn nên thời gian giảm).

Từ tuần 5 đến tuần 6, biểu đồ nằm ngang, nên trong thời gian này, thành tích của cận động viên giữ nguyên là 6,5 phút.

Từ tuần 6 đến tuần 7, thành tích của vận động viên được cải thiện từ 6,5 phút xuống 6 phút.

A=1.21​+3.41​+5.61​+...+99.1001​

\(A = 1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + \frac{1}{5} - \frac{1}{6} + . . . + \frac{1}{99} - \frac{1}{100}\)

\(A = \left(\right. 1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + . . . + \frac{1}{99} + \frac{1}{100} \left.\right) - 2 \left(\right. \frac{1}{2} + \frac{1}{4} + \frac{1}{6} + . . . + \frac{1}{100} \left.\right)\)

\(A = \left(\right. 1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + . . . + \frac{1}{99} + \frac{1}{100} \left.\right) - \left(\right. 1 + \frac{1}{2} + \frac{1}{3} + . . . + \frac{1}{50} \left.\right)\)

\(A = \frac{1}{51} + \frac{1}{52} + \frac{1}{53} + . . . + \frac{1}{100}\)

Tổng \(A\) có \(50\) số hạng, ta có: \(A < \frac{1}{50} . 50 = 1\)

Phân số chỉ số trang sách đọc được trong ngày thứ tư là:

\(1 - \left(\right. \frac{1}{6} + \frac{1}{4} + \frac{1}{5} \left.\right)\)

\(= 1 - \left(\right. \frac{10}{60} + \frac{15}{60} + \frac{12}{60} \left.\right)\)

\(= 1 - \frac{37}{60} = \frac{23}{60}\) (quyển sách)

Phân số chỉ số trang sách đọc được trong hai ngày đầu là:

\(\frac{1}{6} + \frac{1}{4} = \frac{5}{12}\) (quyển sách)

Phân số chỉ số trang sách đọc được trong hai ngày sau là:

\(\frac{1}{5} + \frac{23}{60} = \frac{7}{12}\) (quyển sách)

Hai ngày đầu Bình đọc ít hơn hai ngày sau.

Phân số chỉ số chênh lệch đó là:

\(\frac{7}{12} - \frac{5}{12} = \frac{2}{12} = \frac{1}{6}\) (quyển sách)

Chiều cao của mực nươc trong bể sau khi bỏ thêm hòn đá:

60+5=65 (cm)

Thể tích của tảng đá đó:

(1.60.65)-(1.60.60)=300(cm³)

Vậy thể tích của tảng đá đó là 300 cm³

a) Thể tích của hình hộp chữ nhật đó là:

3.3.5=45(cm³)

Vậy Thể tích của hình hộp chữ nhật đó là 45 cm³

b) Thể tích của hình lăng trụ đứng tứ giác đó là:

(3+4).3:2.5=52,5(cm³)

Diện tích xung quanh của hình lăng trụ đứng tứ giác đó là:

(3+4+3+4).5=70(cm²)

Vậy thể tích và diện tích xung quanh của hình lăng trụ đứng tứ giác đó lần lượt là 52,5 cm³, 70 cm²​

a) \(x + \frac{1}{2} = \frac{6}{4}\)

\(x = \frac{6}{4} - \frac{1}{2}\)

\(x = \frac{6}{4} - \frac{2}{4} = 1\)

b) \(x^{4} \left(. 3\right)^{5} = 27^{3}\)

\(x^{4} \left(. 3\right)^{5} = \left(\left(\right. 3^{3} \left.\right)\right)^{3}\)

\(x^{4} \left(. 3\right)^{5} = 3^{9}\)

\(x^{4} = 3^{9} : 3^{5} = 3^{4}\)

\(x = 3\)

c) \(\frac{8}{3} . \left(\right. \frac{5}{24} - x \left.\right) = \frac{- 1}{3}\)

\(\frac{5}{24} - x = \frac{- 1}{3} : \frac{8}{3}\)

\(\frac{5}{24} - x = \frac{- 1}{8}\)

\(x = \frac{5}{24} + \frac{1}{8} = \frac{8}{24} = \frac{1}{3}\)

a) \(\frac{5}{4} - \left(\left(\right. \frac{1}{2} \left.\right)\right)^{2} = \frac{5}{4} - \frac{1}{4} = 1\)

b) \(\frac{2}{3} . \frac{- 3}{2} + \frac{- 7}{2} . \frac{2}{3}\)

\(= \frac{2}{3} . \left(\right. \frac{- 3}{2} + \frac{- 7}{2} \left.\right)\)

\(=\frac{2}{3}.\left(\right.-5\left.\right)=\frac{- 10}{3}\)

c) \(\left(\right. \frac{1}{5} + \frac{4}{13} \left.\right) + \left(\right. \frac{- 2}{5} + \frac{7}{13} \left.\right) - \left(\right. \frac{4}{5} - \frac{2}{13} \left.\right)\)

\(= \frac{1}{5} + \frac{4}{13} - \frac{2}{5} + \frac{7}{13} - \frac{4}{5} + \frac{2}{13}\)

\(=\left(\right.\frac{1}{5}-\frac{2}{5}-\frac{4}{5}\left.\right)+\left(\right.\frac{4}{13}+\frac{7}{13}+\frac{2}{13}\left.\right)=-1+1=0\)