Phương trình đã cho trở thành

\(\frac{4 x^{2} y^{2}}{\left(\right. x^{2} + y^{2} \left.\right)^{2}} - 1 + \frac{x^{2}}{y^{2}} + \frac{y^{2}}{x^{2}} - 2 \geq 0\)

\(\frac{4 x^{2} y^{2} - \left(\right. x^{2} + y^{2} \left.\right)^{2}}{\left(\right. x^{2} + y^{2} \left.\right)^{2}} + \frac{x^{4} + y^{4} - 2 x^{2} y^{2}}{x^{2} y^{2}} \geq 0\)

\(\frac{- \left(\right. x^{2} - y^{2} \left.\right)^{2}}{\left(\right. x^{2} + y^{2} \left.\right)^{2}} + \frac{\left(\right. x^{2} - y^{2} \left.\right)^{2}}{x^{2} y^{2}} \geq 0\)

\(\left(\right. x^{2} - y^{2} \left.\right)^{2} . \left[\right. \frac{1}{x^{2} y^{2}} - \frac{1}{\left(\right. x^{2} + y^{2} \left.\right)^{2}} \&\text{nbsp}; \left]\right. \geq 0\)

\(\left(\right. x^{2} - y^{2} \left.\right)^{2} . \frac{\left(\right. x^{2} + y^{2} \left.\right)^{2} - x^{2} y^{2}}{x^{2} y^{2} \left(\right. x^{2} + y^{2} \left.\right)^{2}} \geq 0\)

\(\left(\right. x^{2} - y^{2} \left.\right)^{2} . \frac{x^{4} + y^{4} + x^{2} y^{2}}{x^{2} y^{2} \left(\right. x^{2} + y^{2} \left.\right)^{2}} \geq 0\).

Dấu bằng xảy ra khi và chỉ khi \(x = y\) hoặc \(x = - y\).

Chứng minh được: \(\Delta \&\text{nbsp}; A B C \sim \Delta \&\text{nbsp}; H B A\) (g.g)

Từ đó suy ra \(A B^{2} = B C . B H\)

\(\hat{A E D} = \hat{A D E}\) (Cùng phụ với \(\hat{A B D} = \hat{C B D}\))

Suy ra \(\Delta A E D\) cân tại \(A\) suy ra \(A I\) vuông góc với \(D E\) tại \(I\).

Chứng minh \(\Delta E H B\) và \(\Delta E I A\) đồng dạng (g.g).

Từ đó suy ra \(\frac{E I}{E H} = \frac{E A}{E B}\) nên \(E I . E B = E H . E A\).

Gọi \(x\) (km) là quãng đường \(A B\).

Điều kiện: \(x > 0\).

Thời gian người đó đi xe đạp từ \(A\) đến \(B\) là: \(\frac{x}{15}\) (h);

Thời gian lúc về của người đó là: \(\frac{x}{12}\) (h).

Vì thời gian về nhiều hơn thời gian đi \(45\) phút \(= \frac{3}{4}\) (h), nên ta có phương trình:

\(\frac{x}{12} - \frac{x}{15} = \frac{3}{4}\)

\(\frac{5 x}{60} - \frac{4 x}{60} = \frac{45}{60}\)

\(5 x - 4 x = 45\)

\(x = 45\) (TMĐK)

Vậy quãng đường \(A B\) dài \(45\) (km).

a) \(A = \frac{3 x + 15}{x^{2} - 9} + \frac{1}{x + 3} - \frac{2}{x - 3}\) (với \(x \neq 3\), \(x \neq - 3\))

\(A = \frac{3 x + 15}{\left(\right. x + 3 \left.\right) \left(\right. x - 3 \left.\right)} + \frac{1}{x + 3} - \frac{2}{x - 3}\)

\(A = \frac{3 x + 15 + x - 3 - 2 x - 6}{\left(\right. x + 3 \left.\right) \left(\right. x - 3 \left.\right)}\)

\(A = \frac{2 x + 6}{\left(\right. x + 3 \left.\right) \left(\right. x - 3 \left.\right)}\)

\(A = \frac{2}{x - 3}\).

b) Để \(A = \frac{2}{3}\) thì \(\frac{2}{x - 3} = \frac{2}{3}\)

\(x - 3 = 3\)

\(x = 6\) (thỏa mãn điều kiện).

Vậy \(x = 6\) thì \(A = \frac{2}{3}\).

Ta có \(x^{2} - 4 x + 9 = \left(\right. x - 2 \left.\right)^{2} + 5 \geq 5\).

Suy ra \(B = \frac{1}{x^{2} - 4 x + 9} = \frac{1}{\left(\right. x - 2 \left.\right)^{2} + 5} \leq \frac{1}{5}\).

Dấu bằng xảy ra khi \(x = 2\).

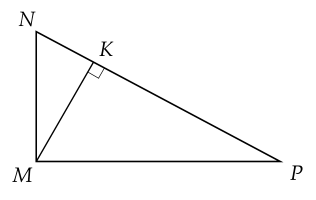
a) Xét \(\Delta K N M\) và \(\Delta M N P\) có:

     \(\hat{M K N} = \hat{N M P} = 9 0^{\circ}\);

     \(\hat{N}\) chung;

Suy ra \(\Delta K N M \sim \Delta M N P\) (g.g) (1)

Xét \(\Delta K M P\) và \(\Delta M N P\) có:

     \(\hat{M K P} = \hat{N M P} = 9 0^{\circ}\)

    \(\hat{P}\) là góc chung

Do đó \(\Delta K M P \sim \Delta M N P\) (g.g) (2)

Từ (1) và (2) suy ra \(\Delta K N M \sim \Delta K M P\).

b) Theo câu a \(\Delta K N M \sim \Delta K M P\).

Từ đây ta có tỉ lệ thức: \(\frac{M K}{K P} = \frac{N K}{M K}\)

Nên \(M K . \&\text{nbsp}; M K = N K . K P\) hay \(M K^{2} = N K . K P\)

c) Từ câu b, ta tính được \(M K = 6\) cm.

Nên \(S_{M N P} = \frac{1}{2} M K . N P = \frac{1}{2} . 6. \left(\right. 4 + 9 \left.\right) = 39\) cm\(^{2}\).

a) Rút gọn \(A = \frac{\left(\right. x - 1 \left.\right)^{2}}{\left(\right. x - 1 \left.\right) \left(\right. x + 1 \left.\right)} = \frac{x - 1}{x + 1}\).

b) Với \(x = 3\) thì \(A = \frac{3 - 1}{3 + 1} = \frac{1}{2}\)

Với \(x = \frac{3}{2}\) thì \(A = \frac{- \frac{3}{2} - 1}{- \frac{3}{2} + 1} = 5\)

c) Ta có biến đối: \(A = \frac{x - 1}{x + 1} = 1 + \frac{- 2}{x + 1}\).

Để biểu thức \(A\) nguyên khi \(\frac{- 2}{x + 1}\) hay \(x + 1\) là ước của \(- 2\).

Do đó

Đối chiếu điều kiện ta thấy \(x\) có giá trị \(- 2 ; - 3 ; 0\) thì biểu thức \(A\) nguyên.

a) \(7 x + 2 = 0\)

\(7 x = - 2\)

\(x = - \frac{2}{7}\).

b) \(18 - 5 x = 7 + 3 x\)

\(- 5 x - 3 x = 7 - 18\)

\(- 8 x = - 11\)

\(x = \frac{11}{8}\).

Question 1: Yes, I like surfing the net because I can find interesting information and watch videos. 

Question 2: I like spending time with other people because it's fun to talk and play together.

Question 3: Yes, I am in the football club. We practise every week. 

Question 4: I like the people in my town because they are friendly and always ready to help. 

Question 5: I feel pressure when I have many homework assignments and exams.

Question 6: I relax by listening to music or talking to my friends. They often give me useful advice to deal with challenges.

Topic 1: One of my favourite leisure activities is playing football. I usually play football twice a week, on the weekends and sometimes after school. I enjoy it a lot because it’s a great way to stay active and healthy. I usually play with my friends at the local park, and we have a lot of fun together. It’s also a good way to relax after a busy week of studying. Playing football helps me improve my teamwork skills because we have to work together to win the game. I like the competition and trying to get better each time. That’s why football is my favourite way to spend my free time.

Topic 2: I would like to join the school’s art club. In this club, students do all kinds of creative activities, like drawing, painting, and making crafts. I think joining the art club would help me improve my drawing skills, which is something I really enjoy. It would also give me a chance to meet other students who like art, so we could share ideas and learn from each other. I want to be a member of this club because I love expressing myself through art, and it would be a fun way to do that. Plus, it would help me relax and take a break from studying.

Topic 3: Last year, I visited a small village called Cổ Loa. It is located just outside Hanoi, in northern Vietnam. The village is very old and has a lot of history. I liked the peaceful atmosphere there because it was very quiet, with not much traffic like in the city. There were also many green fields and traditional houses, which made the place feel calm and beautiful. One thing I didn’t like was that there weren’t many shops or places to eat, so it was hard to find food or buy things. But overall, it’s a good place to live if you like a quiet and simple life. It’s not for everyone, but it’s perfect for people who enjoy peace and nature.