*Dạng thiếu:

if <điều kiện> then <câu lệnh>;

VD: if a>b then write(a);

HĐ: Nếu điều kiện đúng thì thực hiện câu lệnh, điều kiện sai thì kết thúc.

*Dạng đủ:

if <điều kiện> then <câu lệnh 1> else <câu lệnh 2>;

VD: if a>b then write(a) else write(b);

HĐ: Nếu điều kiện đúng thì thực hiện câu lệnh 1 ngược lại thực hiện câu lệnh 2 và kết thúc.

*Dạng thiếu:

if <điều kiện> then <câu lệnh>;

VD: if a>b then write(a);

HĐ: Nếu điều kiện đúng thì thực hiện câu lệnh, điều kiện sai thì kết thúc.

*Dạng đủ:

if <điều kiện> then <câu lệnh 1> else <câu lệnh 2>;

VD: if a>b then write(a) else write(b);

HĐ: Nếu điều kiện đúng thì thực hiện câu lệnh 1 ngược lại thực hiện câu lệnh 2 và kết thúc.

(x - a)/bc + (x - b)/ca + (x - c)/ab = 2/a + 2/b + 2/c

a(x - a) + b(x - b) + c(x - c) = 2bc + 2ac + 2ab

ax - a² + bx - b² + cx - c² = 2bc + 2ac + 2ab

(a + b + c)x = a² + b² + c² + 2bc + 2ac + 2ab

(a + b + c)x = (a + b + c)²

x = (a + b + c)²/(a + b + c)

x = a + b + c

Vậy S = {a + b + c}

a) Chứng minh tam giác ABE đồng dạng tam giác ACF. Suy ra \(A B \cdot A F = A C \cdot A E\)

Chứng minh đồng dạng:

• Xét hai tam giác \(\triangle A B E\) và \(\triangle A C F\):
• • \(\angle A B E = 90^{\circ}\) (do BE là đường cao)
  • \(\angle A C F = 90^{\circ}\) (do CF là đường cao)
  • Cùng góc \(\angle A\) là góc chung

⟹ \(\triangle A B E sim \triangle A C F\) (g.g)

Suy ra tỉ số đồng dạng:

\(\frac{A B}{A C} = \frac{A E}{A F} \Rightarrow A B \cdot A F = A C \cdot A E\)

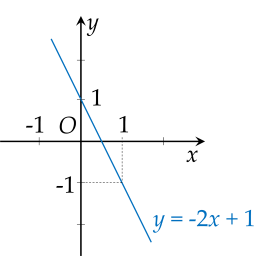
a) Với \(m = - 1\), hàm số trở thành \(y = - 2 x + 1\).

Xét hàm số \(y = - 2 x + 1\) :

Thay \(x = 0\) thì \(y = 1\).

Suy ra đồ thị hàm số \(y = - 2 x + 1\) đi qua điểm có tọa độ \(\left(\right. 0 ; 1 \left.\right)\).

Thay \(x = 1\) thì \(y = - 1\).

Suy ra đồ thị hàm số \(y = - 2 x + 1\) đi qua điểm có tọa độ \(\left(\right. 1 ; - 1 \left.\right)\).

Vẽ đồ thị:

b) Vì đường thẳng \(\left(\right. d \left.\right) : y = a x + b\) song song với đường thẳng \(\left(\right. d^{'} \&\text{nbsp}; \left.\right) : y = - 3 x + 9\) nên: \(a \neq - 3 ; b \neq 9\).

Khi đó ta có: \(\left(\right. d \left.\right) : y = - 3 x + b\) và \(b \neq 9\).

Vì đường thẳng \(\left(\right. d \left.\right) : y = a x + b\) đi qua \(A \left(\right. 1 ; - 8 \left.\right)\) nên: \(- 8 = - 3.1 + b\)

Suy ra \(b = - 5\) (thoả mãn)

Vậy đường thẳng cần tìm là \(\left(\right. d \left.\right) : y = - 3 x - 5\).

Gọi x (h) là thời gian người đó đi từ thành phố về quê (x > 0)

20 phút = 1/3 h

Thời gian người đó đi từ quê lên thành phố là: x + 1/3 (h)

Quãng đường đi từ thành phố về quê: 30x (km)

Quãng đường đi từ quê lên thành phố: 25(x + 1/3) (km)

Theo đề bài, ta có phương trình:

30x = 25(x + 1/3)

30x = 25x + 25/3

30x - 25x = 25/3

5x = 25/3

x = 25/3 : 5

x = 5/3 (nhận)

Vậy quãng đường từ thành phố về quê là: 30 . 5/3 = 50 km

a) 3x - 5 = 4

3x = 4 + 5

3x = 9

x = 9 : 3

x = 3

Vậy S = {3}

b) 2x/3 + (3x - 1)/6 = x/2

4x + 3x - 1 = 3x

7x - 3x = 1

4x = 1

x = 1/4

Vậy S = {1/4}