

Vương Gia Vinh
Giới thiệu về bản thân



































a) \(\frac{5}{17} - \frac{25}{31} + \frac{12}{17} + \frac{- 6}{31}\)
\(= \frac{5}{17} - \frac{25}{31} + \frac{12}{17} + \frac{- 6}{31}\)
\(= \left(\right. \frac{5}{17} + \frac{12}{17} \left.\right) + \left(\right. - \frac{25}{31} + \frac{- 6}{31} \left.\right)\)
\(= 1 + \left(\right. - 1 \left.\right)\)
\(= \&\text{nbsp}; 0\)
b) \(\frac{17}{8} : \left(\right. \frac{27}{8} + \frac{11}{4} \left.\right)\)
\(= \frac{17}{8} : \left(\right. \frac{27}{8} + \frac{22}{8} \left.\right)\)
\(= \frac{17}{8} : \frac{49}{8}\)
\(= \frac{17}{49}\).
c) \(\frac{1}{5} \cdot \frac{11}{16} + \frac{1}{5} \cdot \frac{5}{16} + \frac{4}{5}\)
\(= \frac{1}{5} \cdot \left(\right. \frac{11}{16} + \frac{5}{16} \left.\right) + \frac{4}{5}\)
\(= \frac{1}{5} \cdot 1 + \frac{4}{5}\)
\(= \frac{1}{5} + \frac{4}{5} = 1.\)
d) \(\frac{5}{6} : 25 - 2 + \frac{- 7}{3} \cdot \frac{2}{7}\)
\(= \frac{5}{6} : 25 - 2 + \frac{- 7}{3} \cdot \frac{2}{7}\)
\(= \frac{5}{6} \cdot \frac{1}{25} - 2 + \frac{- 2}{3}\)
\(= \frac{1}{30} - 2 + \frac{- 2}{3}\)
\(= \frac{1}{30} - \frac{60}{30} + \frac{- 20}{30}\)
\(= \frac{1}{30} - \frac{60}{30} + \frac{- 20}{30} = \frac{- 79}{30}\)
1. a) O thuộc các đoạn thẳng: .AB; CD; OA; OB; OC; OD.
b) Ta có O nằm giữa hai điểm A và B vOA = OB =3 cm nên O là trung điểm của đoạn thẳng AB.
2. a) Số đo góc xOy bằng \(3 0^{\circ}\).
b) 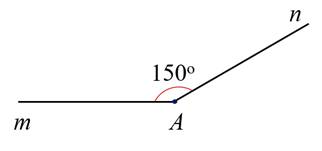
a) Số lượng bóng rổ bán được trong tháng 1, tháng 2, tháng 3 lần lượt là:
\(15\) quả; \(20\) quả; \(10\) quả.
b) Cả ba tháng cửa hàng bán được:
\(15 + 20 + 10 = 45\) (quả)
c) Tháng 2 cửa hàng bán được nhiều hơn tháng 3:
\(20 – 10 = 10\) (quả)
d) Tỉ số giữa số lượng bóng bán được trong tháng 1 và tháng 2 là:
\(3 : 4 = \frac{3}{4}\)
+ \(S=\frac{1}{31}+\frac{1}{32}+\frac{1}{33}+\ldots+\frac{1}{60}\)
\(S<\left(\right.\frac{1}{30}+\frac{1}{30}+\ldots+\frac{1}{30}\left.\right)+\left(\right.\frac{1}{40}+\frac{1}{40}+\ldots+\frac{1}{40}\left.\right)+\left(\right.\frac{1}{50}+\frac{1}{50}+\ldots+\frac{1}{50}\left.\right)\)
\(S<\frac{10}{30}+\frac{10}{40}+\frac{10}{50}<\frac{48}{60}=\frac{4}{5};\)
+ \(S>\left(\right.\frac{1}{40}+\frac{1}{40}+\ldots+\frac{1}{40}\left.\right)+\left(\right.\frac{1}{50}+\frac{1}{50}+\ldots+\frac{1}{50}\left.\right)+\left(\right.\frac{1}{60}+\frac{1}{60}+\ldots+\frac{1}{60}\left.\right)\)
\(S>\frac{10}{40}+\frac{10}{50}+\frac{10}{60}>\frac{3}{5}.\)
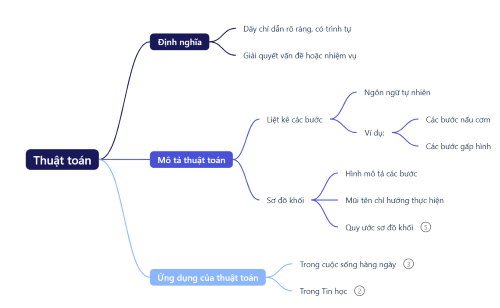
Một số công việc trong thực tế là: luộc rau muống
Đầu vào: rau muống, nước
Đầu ra: món rau muống luộc
Mô tả thuật toán:
1. Lấy 2 lít nước vào xoong.
2. Đun sôi nước.
3. Cho rau đã được rửa sạch vào nước sôi.
4. Chờ rau sôi khoảng 3 phút thì tắt bếp.
Món rau luộc được bày ra đĩa.
Thuật toán giải phương trình bậc nhất:
Bước 1: Nhập a, b;
Bước 2: Nếu a = 0, B≠ 0 thì thông báo vô nghiệm rồi kết thúc;
Bước 3: Nếu a = 0, B = 0 thì thông báo phương trình nghiệm đúng với mọi giá trị rồi kết thúc;
Bước 4: Nếu a ≠ 0 thì x = -b/a thông báo phương trinh có nghiệm duy nhất là x rồi kết thúc