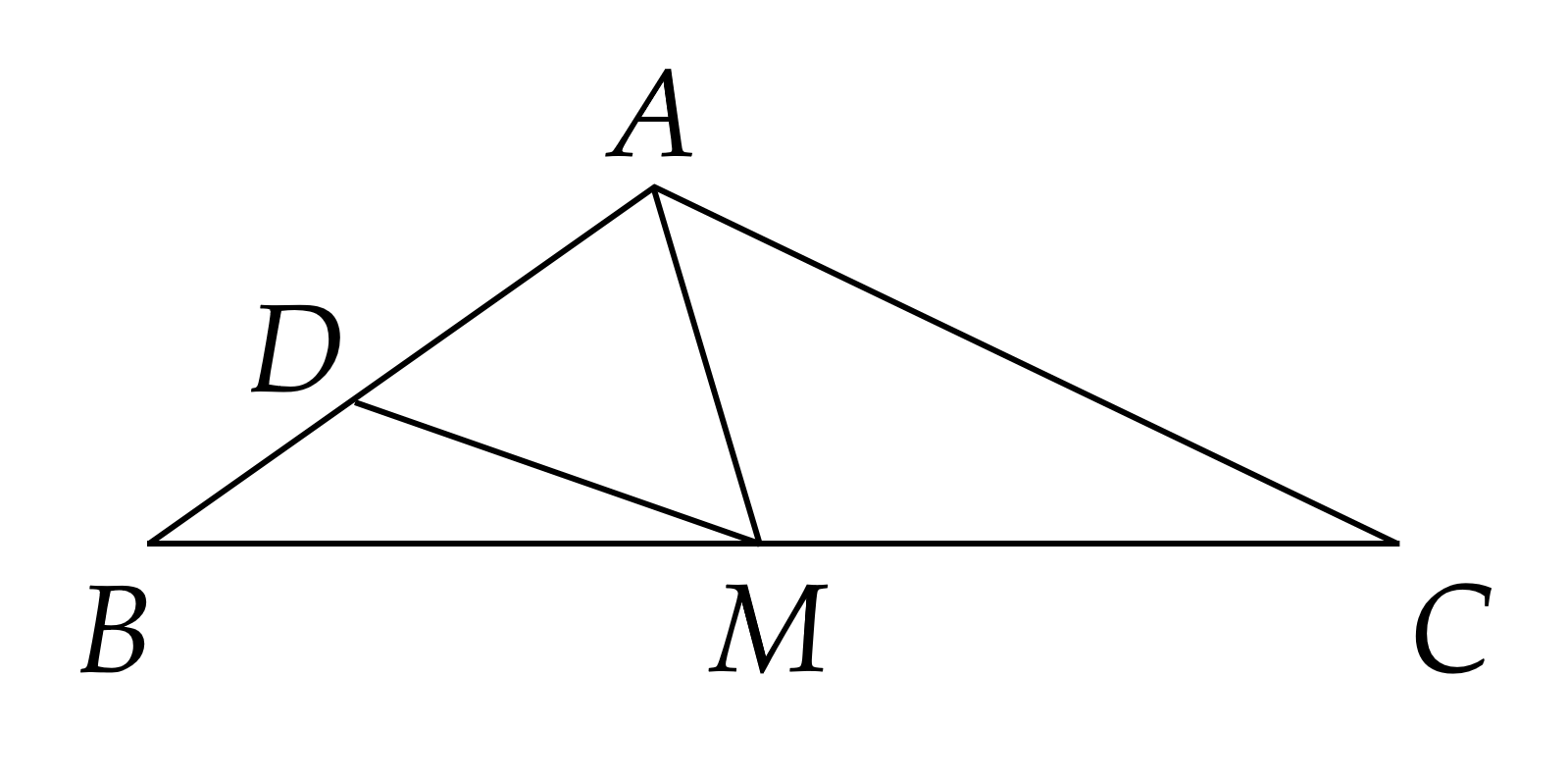
Ta có: \(A B = A D + D B\)

Suy ra \(D B = A B - A D = 10 - 6 = 4\) cm

\(A M\) là trung tuyến của \(\Delta A B C\) suy ra \(M\) là trung điểm của \(B C\)

Suy ra \(B M = C M = \frac{1}{2} B C = 15\) cm.

 Xét \(\Delta A B M\) có \(M D\) là phân giác của góc \(A M B\) nên

\(\frac{A M}{B M} = \frac{A D}{D B}\)

\(\frac{A M}{B M} = \frac{6}{4} = \frac{3}{2}\)

Do đó \(A M = \frac{3}{2} . B M = \frac{3}{2} . 15 = 22 , 5\) (cm).

Ta có: \(A B = A D + D B\)

Suy ra \(D B = A B - A D = 10 - 6 = 4\) cm

\(A M\) là trung tuyến của \(\Delta A B C\) suy ra \(M\) là trung điểm của \(B C\)

Suy ra \(B M = C M = \frac{1}{2} B C = 15\) cm.

 Xét \(\Delta A B M\) có \(M D\) là phân giác của góc \(A M B\) nên

\(\frac{A M}{B M} = \frac{A D}{D B}\)

\(\frac{A M}{B M} = \frac{6}{4} = \frac{3}{2}\)

Do đó \(A M = \frac{3}{2} . B M = \frac{3}{2} . 15 = 22 , 5\) (cm).

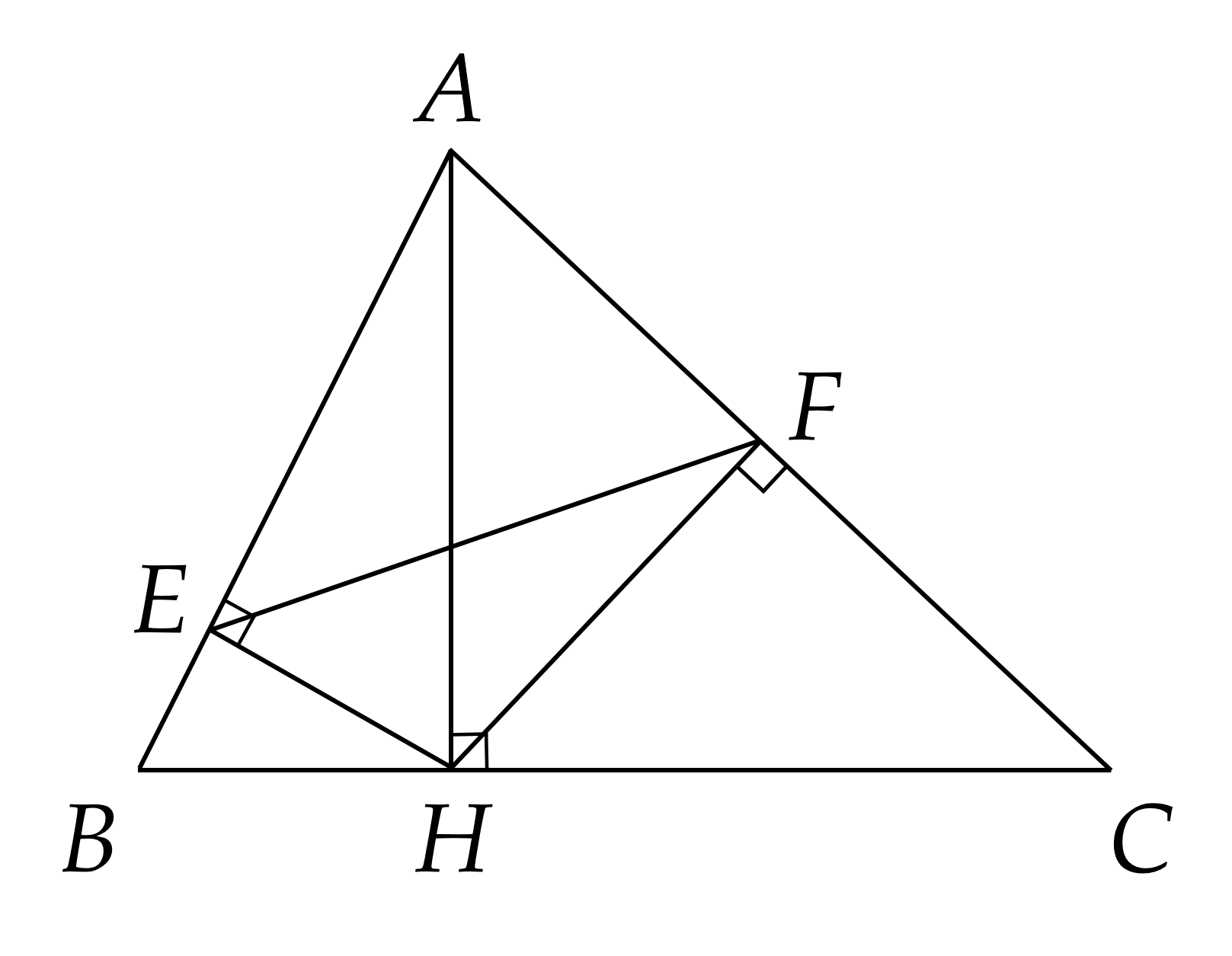
a) Xét \(\Delta A E H\) và \(\Delta A H B\) có:

\(\hat{B A H}\) chung và \(\hat{A E H} = \hat{A H B} = 9 0^{\circ}\)

Do đó \(\Delta A E H \sim \Delta A H B\) (g.g)

Suy ra \(\frac{A H}{A B} = \frac{A E}{A H}\) hay \(A H^{2} = A E . A B\) (1)

b) Chứng minh tương tự \(\Delta A H F \sim \Delta A C H\) (g.g) 

Suy ra \(\frac{A H}{A C} = \frac{A F}{A H}\) hay \(A H^{2} = A F . A C\) (2)

Từ (1) và (2) suy ra \(A E . A B = A F . A C\)

c) Ta có \(A E . A B = A F . A C\) nên \(\frac{A E}{A C} = \frac{A F}{A B}\).

Xét \(\Delta A E F\) và \(\Delta A C B\) có:

\(\hat{E A F}\) chung

\(\frac{A E}{A C} = \frac{A F}{A B}\) (cmt)

Do đó \(\Delta A E F \&\text{nbsp}; \sim \Delta A C B\) (c.g.c).

Suy ra \(\frac{E F}{C B} = \frac{P_{A E F}}{P_{A C B}} = \frac{20}{30} = \frac{2}{3}\) (tỉ số chu vi bằng tỉ số đồng dạng)

Áp dụng tính chất dãy tỉ số bằng nhau ta có \(\frac{S_{A E F}}{4} = \frac{S_{A C B}}{9} = \frac{S_{A C B} - S_{A E F}}{9 - 4} = \frac{25}{5} = 5\)

Suy ra

\(S_{A E F} = 5.4 = 20\) cm\(^{2}\);

\(S_{A C B} = 5.9 = 45\) cm\(^{2}\).

Vậy \(S_{A E F} = 20\) cm\(^{2}\) và \(S_{A C B} = 45\) cm\(^{2}\).

Xác suất cho biến cố "Thẻ rút ra là thẻ đánh số 3" là: \(\frac{6}{20} = \frac{3}{10}\).

Gọi vận tốc riêng của ca nô là \(x\) (km/h, \(x > 3\)).

Vận tốc ca nô khi đi xuôi khúc sông từ \(A\) đến \(B\) là: \(x + 3\)(km/h);

Vận tốc ca nô khi đi ngược khúc sông từ \(B\) về \(A\) là: \(x - 3\)(km/h);

Khúc sông \(A B\) có chiều dài không đổi nên ta có phương trình: \(\frac{3}{2} \left(\right. x + 3 \left.\right) = 2 \left(\right. x - 3 \left.\right)\).

Giải phương trình trên ta nhận được \(x = 21\) (thỏa mãn)

Do đó vận tốc riêng của ca nô là \(21\) km/h.

Chiều dài khúc sông là: \(2 \left(\right. 21 - 3 \left.\right) = 36\) (km).

Vậy vận tốc riêng của cano là \(21\) km/h, chiều dài khúc sông là \(36\) km .

a. Ta có: \(3 x - 4 = 5 + x\)

\(3 x - x = 5 + 4\)

\(2 x = 9\)

\(x = \frac{9}{2}\).

Vậy phương trình đã cho có nghiệm \(x = \frac{9}{2}\).

b. Ta có: \(3 \left(\right. x - 1 \left.\right) - 7 = 5 \left(\right. x + 2 \left.\right)\)

\(3 x - 3 - 7 = 5 x + 10\)

\(5 x - 3 x = - 3 - 7 - 10\)

\(2 x = - 20\)

\(x = - 10\).

Vậy phương trình có nghiệm \(x = - 10\).

Bài làm:

Trong kho tàng văn hóa dân gian Việt Nam, những câu tục ngữ thường chứa đựng những bài học quý giá về cách sống và cách ứng xử trong cuộc sống. Một trong những câu tục ngữ đáng chú ý là "Giấy rách phải giữ lấy lề". Mặc dù chỉ là một câu ngắn gọn, nhưng ý nghĩa của câu tục ngữ này lại rất sâu sắc và có giá trị lớn trong việc giáo dục con người, giúp mỗi chúng ta hiểu rõ hơn về cách đối mặt với khó khăn, giữ gìn những giá trị quan trọng trong cuộc sống.

Trước hết, chúng ta cần hiểu câu tục ngữ này từ góc độ nghĩa đen. "Giấy rách phải giữ lấy lề" có nghĩa là khi tờ giấy bị rách, dù không thể sửa chữa lại hoàn hảo như ban đầu, nhưng người ta vẫn cần phải giữ gìn phần lề của nó. Phần lề dù nhỏ nhưng vẫn có giá trị nhất định, giúp bảo vệ và giữ lại sự nguyên vẹn cho tờ giấy. Hình ảnh này ẩn dụ cho việc, trong cuộc sống, dù gặp phải những thất bại hay khó khăn, chúng ta vẫn cần biết giữ gìn những gì quan trọng, những giá trị cốt lõi mà không thể đánh mất.

Về mặt ý nghĩa sâu xa, câu tục ngữ này khuyên chúng ta rằng, khi gặp phải những khó khăn, thử thách trong cuộc sống, dù mọi thứ có thể không còn hoàn hảo, chúng ta vẫn cần bảo vệ những điều quan trọng nhất, những giá trị không thể thiếu. Đó có thể là gia đình, tình bạn, tình yêu, hay những nguyên tắc đạo đức mà chúng ta đã học được. Mỗi khi đối mặt với gian nan, thay vì buông xuôi, chúng ta cần biết giữ gìn và trân trọng những giá trị ấy, dù chúng có thể không còn nguyên vẹn như trước.

Câu tục ngữ "Giấy rách phải giữ lấy lề" cũng thể hiện một tinh thần kiên cường, không dễ dàng bỏ cuộc. Cuộc sống không phải lúc nào cũng suôn sẻ và thuận lợi, đôi khi chúng ta sẽ gặp phải thất bại, vấp ngã. Tuy nhiên, thay vì đầu hàng, chúng ta phải biết đứng dậy và bảo vệ những gì còn lại, dù đó chỉ là những điều nhỏ bé nhưng hết sức quan trọng. Chính trong những lúc khó khăn đó, chúng ta cần biết nắm giữ những giá trị tinh thần như lòng kiên nhẫn, sự yêu thương và sự tôn trọng đối với bản thân và mọi người xung quanh.

Đặc biệt, câu tục ngữ còn nhắc nhở chúng ta về sự trân trọng những giá trị không hoàn hảo. Mỗi người đều có những sai lầm, thiếu sót, nhưng chính những thiếu sót ấy tạo nên sự đa dạng và phong phú trong cuộc sống. Việc chấp nhận và bảo vệ những điều không hoàn hảo chính là cách để chúng ta học hỏi và trưởng thành. Cũng giống như tờ giấy rách, mặc dù không còn nguyên vẹn, nhưng nếu chúng ta biết giữ gìn, nó vẫn có giá trị và ý nghĩa riêng.

Hơn nữa, câu tục ngữ này còn đề cao tính kiên nhẫn và sự kiên trì trong cuộc sống. Khi gặp phải thất bại hay khó khăn, chúng ta không nên dễ dàng từ bỏ. Dù mọi thứ có thể không như ý muốn, nhưng nếu chúng ta kiên trì và cố gắng, thì dù là những điều nhỏ bé nhất cũng có thể mang lại giá trị. Đó chính là thông điệp mà câu tục ngữ muốn truyền đạt: dù gặp phải khó khăn, vẫn phải giữ lấy những điều quan trọng và kiên định với những giá trị mà mình tin tưởng.

Cuối cùng, câu tục ngữ "Giấy rách phải giữ lấy lề" chính là lời nhắc nhở mỗi chúng ta về sự quan trọng của việc bảo vệ những giá trị tinh thần và tình cảm trong cuộc sống. Dù đối mặt với khó khăn, thất bại hay mất mát, chúng ta không nên để mình bị suy sụp hoàn toàn, mà phải biết bảo vệ những giá trị còn lại, dù chúng có nhỏ bé hay không hoàn hảo. Bằng cách đó, chúng ta sẽ luôn tìm thấy ánh sáng và hy vọng trong những lúc tối tăm nhất.0000

Hướng dẫn giải:

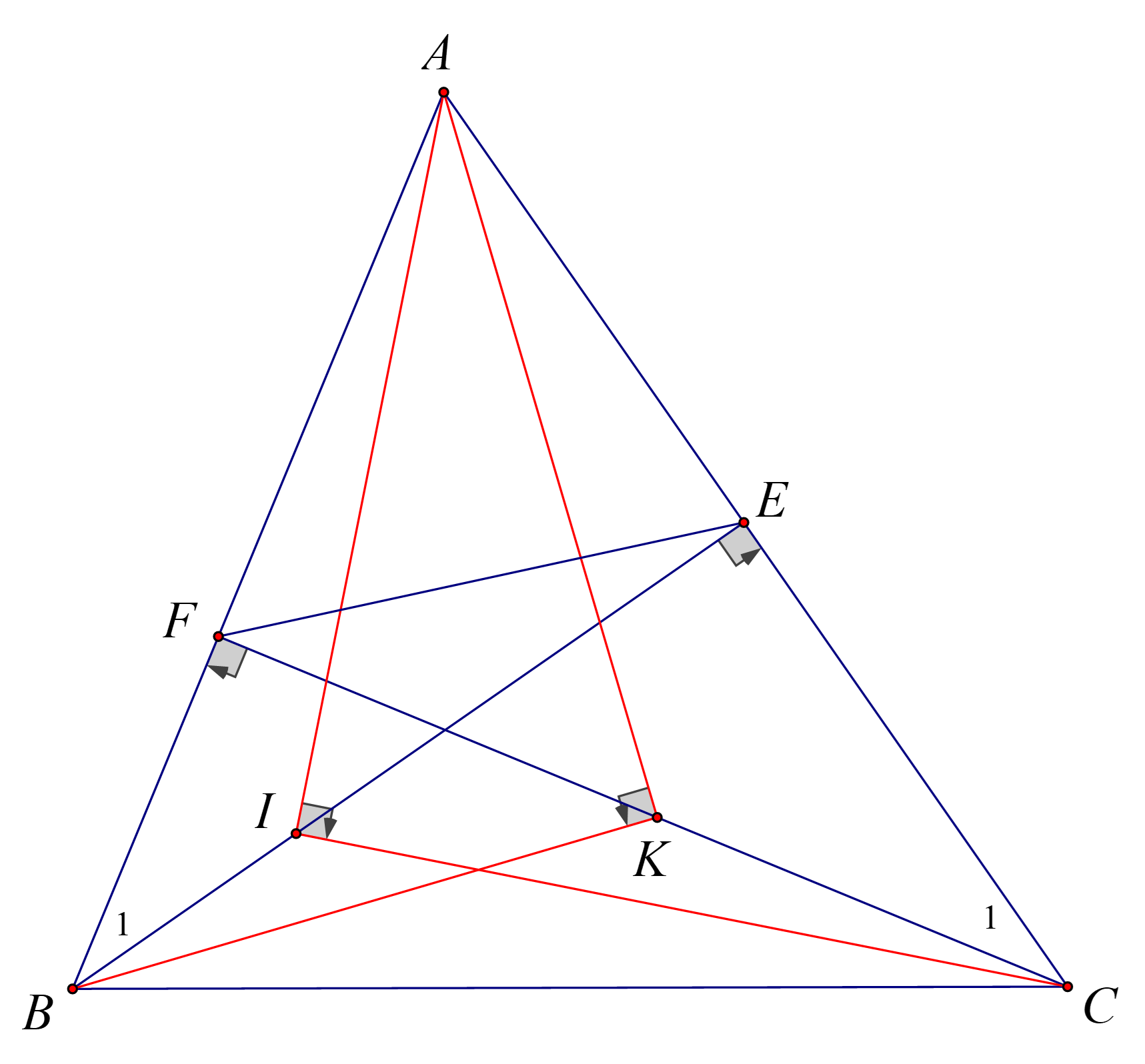
a) \(\Delta A I E \sim \Delta A C I\) (g.g) suy ra \(\frac{A I}{A C} = \frac{A E}{A I}\) hay \(A I^{2} = A E . A C\) (1)

Chứng minh tương tự:

\(\Delta A I K \sim \Delta A K B\) (g.g) suy ra \(\frac{A K}{A B} = \frac{A F}{A K}\) hay \(A K^{2} = A B . A F\) (2)

Mà \(\Delta A B E \sim \Delta A C F\) (g.g) suy ra \(\frac{A B}{A C} = \frac{A E}{A F}\) hay \(A B . A F = A C . A E\) (3)

Từ (1), (2) và (3) ta có \(A I^{2} = A K^{2}\) suy ra \(A I = A K\).

b) Vì \(\hat{A} = 60^{\circ}\) suy ra \(\hat{B_{1}} = 30^{\circ}\)

Trong tam giác \(A B E\) vuông tại \(E\) nên \(A E = \frac{1}{2} A B ,\)

Trong tam giác \(A F C\) vuông tại \(F\) có \(\hat{C_{1}} = 30^{\circ}\) suy ra \(A F = \frac{1}{2} A C\).

Do đó, \(\Delta A E F \sim \Delta A B C\) (c.g.c).

suy ra \(\frac{S_{A E F}}{S_{A B C}} = \left(\left(\right. \frac{A E}{A B} \left.\right)\right)^{2} = \frac{1}{4}\).

Vậy \(S_{A E F} = \frac{1}{4} . 120 = 30\) cm\(^{2}\).

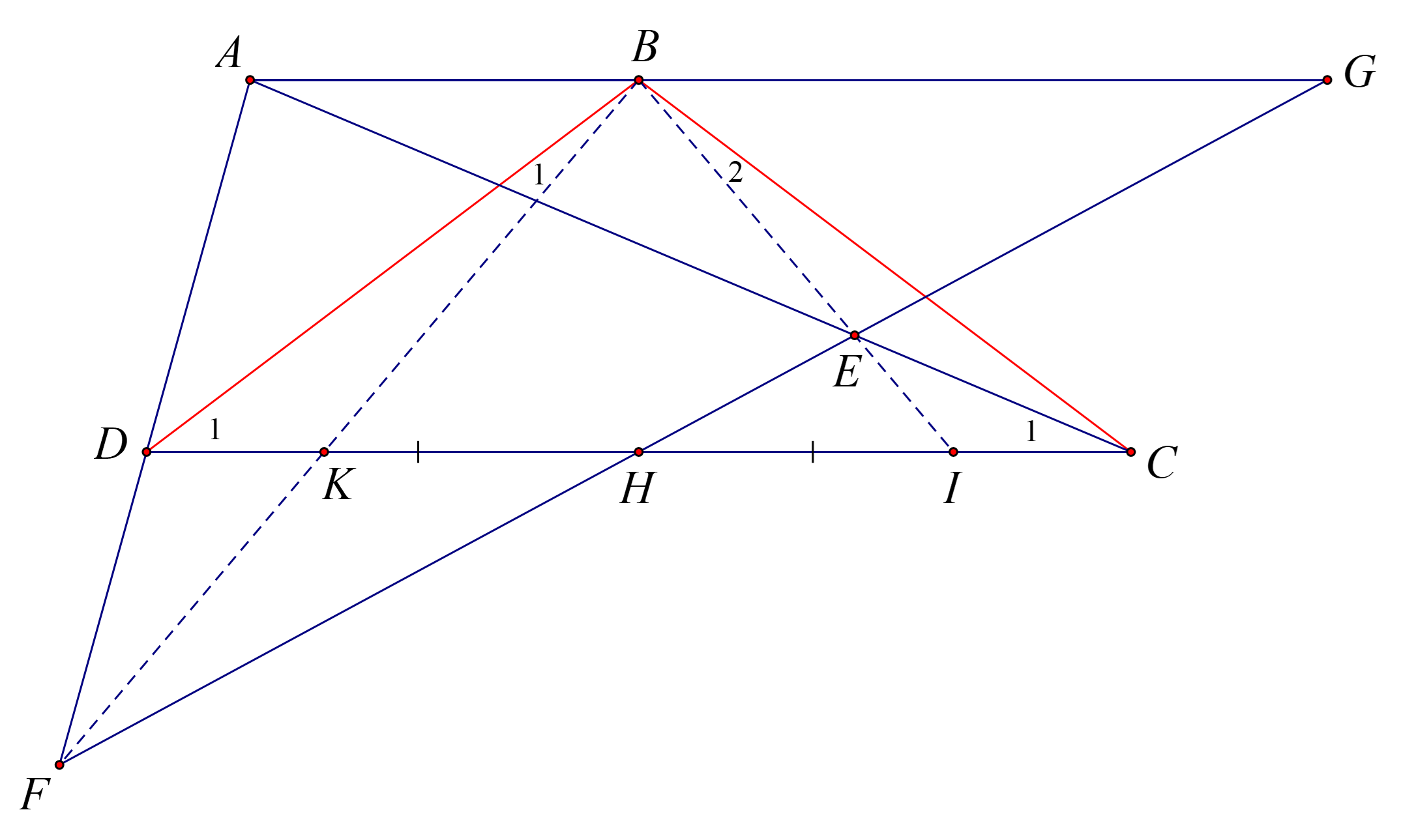
Gọi \(B F\) cắt \(D C\) tại \(K\), \(B E\) cắt \(D C\) tại \(I\), và \(E F\) cắt \(A B\) tại \(G\).

\(\Delta F A B\) có \(D K\) // \(A B\) suy ra \(\frac{D K}{A B} = \frac{F D}{F A}\) (1)

\(\Delta F A G\) có \(D H\) // \(A G\) suy ra \(\frac{D H}{A G} = \frac{F D}{F A}\) (2)

Từ (1) và (2) suy ra \(\frac{D K}{A B} = \frac{D H}{A G}\) hay \(\frac{D K}{D H} = \frac{A B}{A G}\) (*)

Tương tự \(\Delta E I C\) có \(A B\) // \(I C\) suy ra \(\frac{I C}{A B} = \frac{E C}{E A}\) (3)

\(\Delta E H C\) có \(H C\) // \(A B\) suy ra \(\frac{H C}{A G} = \frac{E C}{E A}\) (4)

Từ (3) và (4) ta có \(\frac{I C}{A B} = \frac{H C}{A G}\) hay \(\frac{I C}{H C} = \frac{A B}{A G}\) (**)

Từ (*) và (**) ta có \(\frac{D K}{D H} = \frac{I C}{H C}\).

Mà \(D H = H C\) (gt) suy ra \(D K = I C\)

Mặt khác \(B D = B C\) (gt) nên \(\Delta B D C\) cân

Suy ra \(\hat{B D K} = \hat{B C I}\)

Vậy \(\Delta B D K = \Delta B C I\) (c.g.c)

Suy ra \(\hat{D B K} = \hat{C B I}\).

a) \(\Delta A B E\) có \(A M\) // \(D G\) suy ra \(\frac{A E}{E G} = \frac{E B}{E D}\) (1)

\(\Delta A D E\) có \(A D\) // \(B K\) suy ra \(\frac{E B}{E D} = \frac{E K}{E A}\) (2)

Từ (1) và (2) ta có \(\frac{A E}{E G} = \frac{E K}{E A}\) nên \(A E^{2} = E K . E G\).

b) Từ \(\frac{1}{A E} = \frac{1}{A K} + \frac{1}{A G}\) suy ra \(\frac{A E}{A K} + \frac{A E}{A G} = 1\)

\(\Delta A D E\) có \(A D\) // \(B C\) suy ra \(\frac{A E}{E K} = \frac{E D}{E B}\)

     \(\frac{A E}{A E + E K} = \frac{E D}{E D + E B}\)

     \(\frac{A E}{A K} = \frac{E D}{D B}\) (3)

Tương tự \(\Delta A E B\) có \(A B\) // \(D G\) suy ra \(\frac{A E}{E G} = \frac{B E}{E D}\)

     \(\frac{A E}{A E + E G} = \frac{B E}{B E + E D}\)

     \(\frac{A E}{A G} = \frac{B E}{B D}\) (4)

Khi đó \(\frac{A E}{A K} + \frac{A E}{A G} = \frac{E D}{B D} + \frac{B E}{B D} = 1\).

c) Ta có \(\frac{B K}{K C} = \frac{A B}{C G}\) suy ra \(B K = \frac{K C . A B}{C G}\) và \(\frac{K C}{A D} = \frac{C G}{D G}\).

Suy ra \(D G = \frac{A D . C G}{K C}\)

Nhân theo vế ta được \(B K . D G = A B . A D\) không đổi.