\(\hat{O_{1}} - \hat{O_{2}} = 7 0^{\circ}\);

  \(\hat{O_{1}} + \hat{O_{2}} \&\text{nbsp}; + \hat{O_{3}} = 32 5^{\circ}\).

Hướng dẫn giải:

 Biết \(\hat{O_{1}} - \hat{O_{2}} = 7 0^{\circ}\)

Suy ra \(\hat{O_{1}} = \&\text{nbsp}; \hat{O_{2}} + 7 0^{\circ}\)

Mà \(\hat{O_{1}}\) và \(\hat{O_{2}}\) là hai góc kề bù nên \(\hat{O_{1}} + \&\text{nbsp}; \hat{O_{2}} = 18 0^{\circ}\).

Thay \(\hat{O_{1}} = \&\text{nbsp}; \hat{O_{2}} + 7 0^{\circ}\) ta được \(\hat{O_{2}} + \&\text{nbsp}; \hat{O_{2}} + 7 0^{\circ} = 18 0^{\circ}\)

Hay \(2. \hat{O_{2}} = 11 0^{\circ}\)

Suy ra \(\hat{O_{2}} = 5 5^{\circ}\).

Mà hai góc \(\hat{O_{2}}\) và \(\hat{O_{4}}\) đối đỉnh nên \(\hat{O_{4}} = 5 5^{\circ}\)

 Biết \(\hat{O_{1}} + \hat{O_{2}} \&\text{nbsp}; + \hat{O_{3}} = 32 5^{\circ}\).

Mà \(\hat{O_{1}}\) và \(\hat{O_{2}}\) là hai góc kề bù nên \(\hat{O_{1}} + \&\text{nbsp}; \hat{O_{2}} = 18 0^{\circ}\).

Suy ra \(\hat{O_{3}} = 32 5^{\circ} - 18 0^{\circ} = 14 5^{\circ}\).

Mà \(\hat{O_{3}}\) và \(\hat{O_{4}}\) là hai góc kề bù nên \(\hat{O_{4}} = 18 0^{\circ} - 14 5^{\circ} = 3 5^{\circ}\).

Ta có: \(1^{2} + 2^{2} + 3^{2} + \ldots + 1 0^{2} = 385\)

Suy ra: \(\left(\right. 1^{2} + 2^{2} + 3^{2} + \ldots + 1 0^{2} \left.\right) . 3^{2} = 385. 3^{2}\)

\(\left(\right. 1.3 \left.\right)^{2} + \left(\right. 2.3 \left.\right)^{2} + \left(\right. 3.3 \left.\right)^{2} + \ldots + \left(\right. 10.3 \left.\right)^{2} = 385. 3^{2}\)

Do đó \(A = 3^{2} + 6^{2} + 9^{2} + \ldots + 3 0^{2} = 3465\).

 Ta có \(\hat{C A x} + \hat{B A C} = 18 0^{\circ}\) (hai góc kề bù).

Suy ra: \(\hat{C A x} = 18 0^{\circ} - \hat{B A C}\)

\(\hat{C A x} = 18 0^{\circ} - \&\text{nbsp}; 10 0^{\circ} = 8 0^{\circ}\).

b) Vì \(A y\) là tia phân giác của \(\hat{C A x}\), nên

\(\hat{C A y} = \hat{x A y} = \frac{1}{2} . \hat{C A x} = \frac{1}{2} . 8 0^{\circ} = 4 0^{\circ}\).

Vậy \(\hat{C A y} = \hat{A C B}\), mà hai góc này ở vị trí so le trong, do đó \(A y\) // \(B C\).

c) Do \(A y\) // \(B C\), nên \(\hat{x A y} = \hat{A B C}\) (hai góc đồng vị).

Suy ra \(\hat{A B C} = 4 0^{\circ}\).

​a) \(x - \frac{2}{3} = \frac{1}{6}\)

\(x = \frac{1}{6} + \frac{2}{3}\)

\(x = \frac{1}{6} + \frac{4}{6}\)

\(x = \frac{5}{6}\).

b) \(2 x + \frac{1}{2} = - \frac{5}{3}\)

\(2 x = - \frac{5}{3} - \frac{1}{2}\)

\(2 x = - \frac{13}{6}\)

\(x = - \frac{13}{12}\).

c) \(3 x + \frac{3}{2} = x - \frac{5}{3}\)

\(3 x - x = - \frac{5}{3} - \frac{3}{2}\)

\(2 x = \frac{- 19}{6}\)

\(x = \frac{- 19}{12}\).

 \(​ \frac{11}{24} - \frac{5}{41} + \frac{13}{24} + 0 , 5 - \frac{36}{41} = \left(\right. \frac{11}{24} + \frac{13}{24} \left.\right) - \left(\right. \frac{5}{41} + \frac{36}{41} \left.\right) + 0 , 5 = 1 - 1 + 0 , 5 = 0 , 5\).

b) \(\frac{1}{2} \cdot \frac{3}{4} + \frac{1}{2} \cdot \frac{1}{4} + \frac{1}{2} = \frac{1}{2} \cdot \left(\right. \frac{3}{4} + \frac{1}{4} + 1 \left.\right) = \frac{1}{2} \cdot 2 = 1\).

c) \(\left(\right. \frac{- 3}{4} \left.\right)^{2} : \left(\right. \frac{- 1}{4} \left.\right)^{2} + 9 \cdot \left(\right. \frac{- 1}{9} \left.\right) + \left(\right. \frac{- 3}{2} \left.\right) = \frac{9}{16} : \frac{1}{16} - 1 - \frac{3}{2} = 9 - 1 - \frac{3}{2} = \frac{13}{2} .\)

d) \(\sqrt{0 , 25} \cdot \left(\right. - 3 \left.\right)^{3} - \sqrt{\frac{1}{81}} : \left(\right. \frac{- 1}{3} \left.\right)^{3} = 0 , 5 \cdot \left(\right. - 27 \left.\right) - \frac{1}{9} : \frac{- 1}{27} = \frac{- 27}{2} + 3 = \frac{- 21}{2}\).

Gọi số học sinh lớp \(7 B\) là \(x\) \(\left(\right. x \in \mathbb{N}^{*} \left.\right)\) (học sinh)

Số học sinh ban đầu lớp \(7 A\) là \(\frac{4}{5} x\) (học sinh)

Theo đề bài, ta có: 

 \(\frac{4}{5} x - 8 = \frac{1}{2} \left(\right. x + 8 \left.\right)\)

 \(\frac{4}{5} x - 8 = \frac{1}{2} x + 4\)

\(\frac{3}{10} x = 12\)

\(x = 40\) (thỏa mãn)

Vậy số học sinh là \(7 B\) là \(40\) học sinh

Số học sinh lớp \(7 A\) là: \(40. \frac{4}{5} = 32\) (học sinh)

Tổng số học sinh lớp \(7 A\) và lớp \(7 B\) của một trường là: \(40 + 32 = 72\) (học sinh)

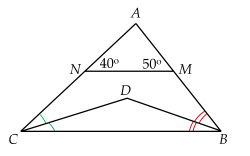
Vì \(M N / / B C\) nên \(\hat{A C B} = \hat{A N M} = 4 0^{\circ}\) và \(\hat{A B C} = \hat{A M N} = 5 0^{\circ}\)

Vì \(C D\) là phân giác góc \(A C B\) nên \(\hat{D C B} = 4 0^{\circ} : 2 = 2 0^{\circ}\)

Vì \(B D\) là phân giác góc \(A B C\) nên \(\hat{D B C} = 5 0^{\circ} : 2 = 2 5^{\circ}\)

Vậy \(\hat{D C B} < \hat{D B C}\)

Góc \(A O D\) và \(B O C\) đối đỉnh, góc \(A O B\) và \(C O D\) đối đỉnh

Diện tích mảnh vườn hình chữ nhật là: \(5.4 = 20\) (m²)

Diện tích mảnh đất trồng hoa là: \(20 - 11 = 9\) (m²)

Cạnh của mảnh đất trồng hoa hình vuông là: \(\sqrt{9} = 3\) (m

a) \(x - \frac{3}{7} = \frac{5}{4}\)

\(x = \frac{5}{4} + \frac{3}{7}\)

\(x = \frac{35}{28} + \frac{12}{28}\)

\(x = \frac{47}{28}\)

b) \(\left(\right. x - \frac{3}{5} \left.\right) : \frac{- 1}{3} = 0 , 4\)

\(x - \frac{3}{5} = 0 , 4. \frac{- 1}{3}\)

\(x - \frac{3}{5} = \frac{- 2}{15}\)

\(x = \frac{- 2}{15} + \frac{3}{5} = \frac{7}{15}\)