B=1.44​+4.74​+7.104​+....+94.974​+97.1004​

\(B = 4 \left(\right. \frac{1}{1.4} + \frac{1}{4.7} + \frac{1}{7.10} + . . . . + \frac{1}{94.97} + \frac{1}{97.100} \left.\right)\)

\(B = \frac{4}{3} \left(\right. \frac{3}{1.4} + \frac{3}{4.7} + \frac{3}{7.10} + . . . . + \frac{3}{94.97} + \frac{3}{97.100} \left.\right)\)

\(B = \frac{4}{3} \left(\right. 1 - \frac{1}{4} + \frac{1}{4} - \frac{1}{7} + \frac{1}{7} - \frac{1}{10} + . . . . + \frac{1}{94} - \frac{1}{97} + \frac{1}{97} - \frac{1}{100} \left.\right)\)

\(B = \frac{4}{3} \left(\right. 1 - \frac{1}{100} \left.\right)\)

\(B = \frac{4}{3} . \frac{99}{100}\)

\(B = \frac{33}{25}\).

Vậy \(B = \frac{33}{25}\).

a) Ta có điểm \(M\) nằm giữa \(O\) và \(A\) \(\left(\right. M\) là trung điểm \(O A \left.\right)\) hay \(M\) và \(A\) cùng phía so với \(O\).

Mặt khác \(A\) thuộc tia \(O x\) nên \(M\) thuộc tia \(O x\).

Tương tự, điểm \(N\) nằm giữa \(O\) và \(B\) \(\left(\right. N\) là trung điểm \(O B \left.\right)\) hay \(N\) và \(B\) cùng phía so với \(O\).

Mặt khác \(B\) thuộc tia \(O y\) nên \(N\) thuộc tia \(O y\).

Mà \(O x\) và \(O y\) là hai tia đối nên \(M\) và \(N\) khác phía so với \(O\).

Vậy \(O\) nằm giữa \(M\) và \(N\).

b) Theo đề bài, ta có \(M\) là trung điểm của \(O A\) nên:

\(O M = M A = \frac{O A}{2} = 3\) cm.

Ta có \(N\) là trung điểm của \(O B\) nên:

\(O N = N B = \frac{O B}{2} = \frac{3}{2} = 1 , 5\) cm.

Vì \(O\) nằm giữa điểm \(M\) và \(N\) nên ta có:

\(O M + O N = M N\) hay \(M N = 3 + 1 , 5 = 4 , 5\) cm.

1. Cân nặng của quả dưa hấu là:

\(2 : \frac{2}{3} = 3\) (kg).

Vậy quả dưa hấu nặng \(3\) kg.

2. Số thí sinh Châu Á dự thi là:

\(152. \frac{7}{19} = 56\) (thí sinh)

Số thí sinh Châu Âu, Châu Phi và Châu Mỹ tham gia dự thi là:

\(152 - 56 = 96\) (thí sinh)

Số thí sinh Châu Âu tham gia dự thi là:

\(96. \frac{5}{8} = 60\) (thí sinh)

Số thí sinh Châu Phi và Châu Mỹ dự thi là:

\(96 - 60 = 36\) (thí sinh)

Số thí sinh Châu Mỹ nhiều hơn số thí sinh Châu Phi là \(8\).

Do đó, số thí sinh Châu Mỹ tham gia dự thi là:

\(\left(\right. 36 + 8 \left.\right) : 2 = 22\) (thí sinh)

Số thí sinh Châu Phi dự thi là:

\(22 - 8 = 14\) (thí sinh)

Vậy Châu Á có \(56\) thí sinh, Châu Âu có \(60\) thí sinh, Châu Mỹ có \(22\) thí sinh, Châu Phi có \(14\) thí sinh.

1.

Do \(A\) là trung điểm \(O B\), nên \(O B = 2. O A\).

Thay số \(O A = 2\) cm, ta có

\(O B = 2.2 = 4\) (cm)

2.

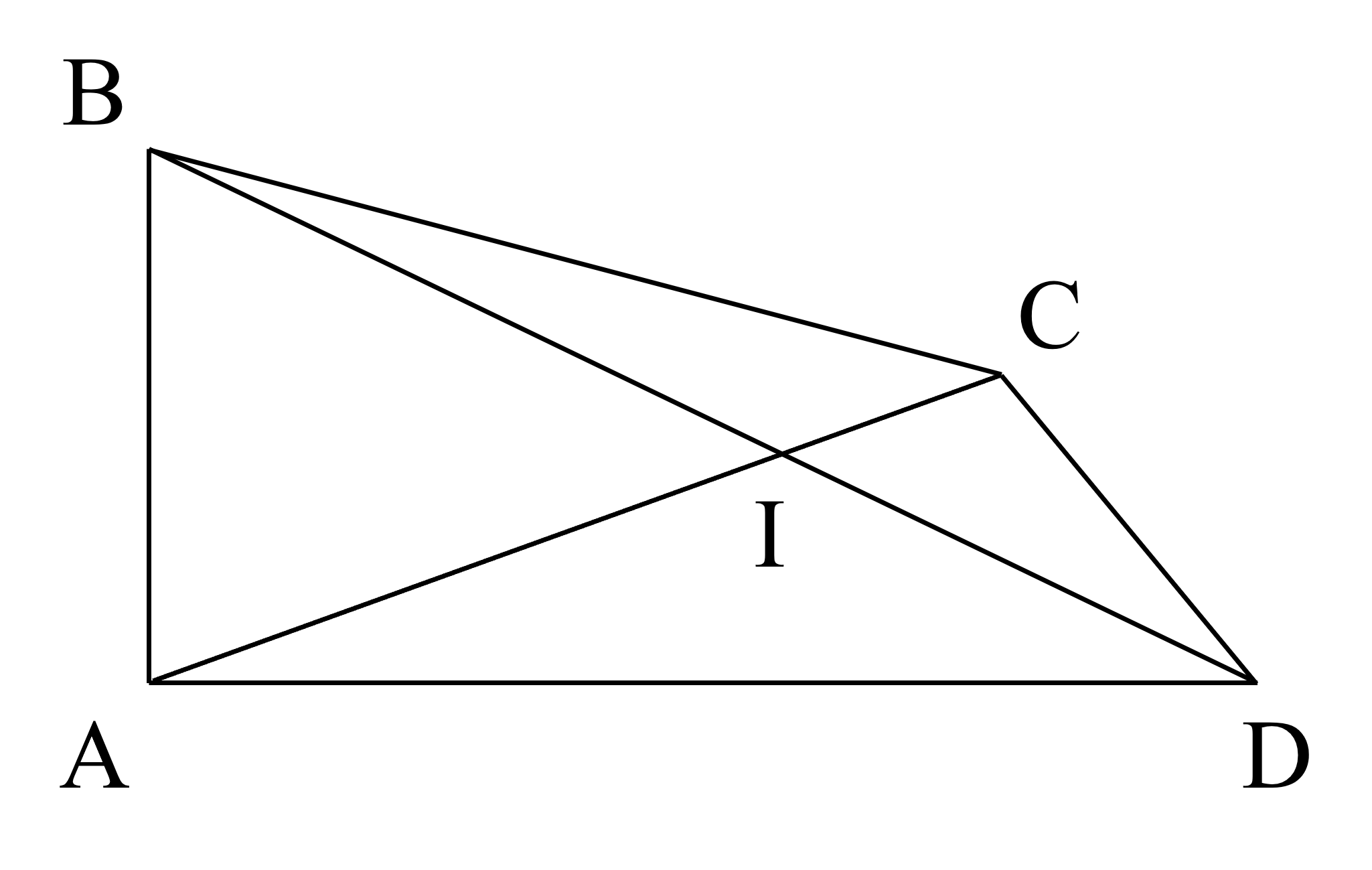
a) Điểm \(C\) và điểm \(I\) nằm trong góc \(B A D\).

b)

Các góc bẹt trong hình là góc \(B I D\) và \(A I C\).

c)

Đo góc, ta lần lượt có các số đo góc như sau:

\(\hat{A I C} = 18 0^{\circ}\)

\(\hat{A C D} = 7 0^{\circ}\)

\(\hat{B C D} = 13 5^{\circ}\)

\(\hat{B A D} = 9 0^{\circ}\)

Sắp xếp các góc theo thứ tự tăng dần về số đo, ta được:

\(\hat{A C D} ; \hat{B A D} ; \hat{B C D} ; \hat{A I C}\).

1.

Do \(A\) là trung điểm \(O B\), nên \(O B = 2. O A\).

Thay số \(O A = 2\) cm, ta có

\(O B = 2.2 = 4\) (cm)

2.

a) Điểm \(C\) và điểm \(I\) nằm trong góc \(B A D\).

b)

Các góc bẹt trong hình là góc \(B I D\) và \(A I C\).

c)

Đo góc, ta lần lượt có các số đo góc như sau:

\(\hat{A I C} = 18 0^{\circ}\)

\(\hat{A C D} = 7 0^{\circ}\)

\(\hat{B C D} = 13 5^{\circ}\)

\(\hat{B A D} = 9 0^{\circ}\)

Sắp xếp các góc theo thứ tự tăng dần về số đo, ta được:

\(\hat{A C D} ; \hat{B A D} ; \hat{B C D} ; \hat{A I C}\).

a) \(\frac{1}{2} - \frac{1}{2} : x = \frac{3}{4}\)

\(\frac{1}{2} : x = \frac{1}{2} - \frac{3}{4}\)

\(\frac{1}{2} : x = \frac{- 1}{4}\)

\(x=\frac{1}{2}:\frac{- 1}{4}\)

\(x = - 2\)

b) \(\frac{x - 1}{15} = \frac{3}{5}\)

\(\frac{x - 1}{15} = \frac{9}{15}\)

\(x - 1 = 9\)

\(x = 10\)

c) \(x + 2 , 5 = 1 , 4\)

\(x = 1 , 4 - 2 , 5\)

\(x = - 1 , 1\)

a) \(A = 2 , 34 + 5 , 35 + 7 , 66 + 4 , 65\)

\(= \left(\right. 2 , 34 + 7 , 66 \left.\right) + \left(\right. 4 , 65 + 5 , 35 \left.\right)\)

\(= 10 + 10\)

\(= 20\)

b) \(B = 2 , 13.75 + 2 , 13.25\)

\(= 2 , 13. \left(\right. 75 + 25 \left.\right)\)

\(= 2 , 13.100\)

\(= 213\)

c) \(C = \frac{1}{3} - \frac{1}{3} : \frac{3}{4}\)

\(=\frac{1}{3}-\frac{1}{3}.\frac{4}{3}\)

\(= \frac{1}{3} - \frac{4}{9}\)

\(= \frac{3}{9} - \frac{4}{9}\)

\(= \frac{- 1}{9}\)

ByxAMCz

a) Các tia chung gốc \(A\) là:

   \(A B\) (hay \(A y\)); \(A M\) (hay \(A C\), \(A z\)); \(A x\).

b) Các điểm thuộc tia \(A z\) mà không thuộc tia \(A y\) là:

   \(M\) và \(C\).

c) Tia \(A M\) và tia \(M A\) không chung gốc nên không phải hai tia đối nhau.

Số tiền \(15\) quyển vở trước khi giảm giá là:

\(15.7\) \(000 = 105\) \(000\) (đồng)

Số tiền \(15\) quyển vở sau khi giàm giá \(10 \%\) là:

\(105\) \(000.90 \% = 94\) \(500\) (đồng)

Vậy bạn An đem theo \(100\) \(000\) đồng nên đủ tiền mua \(15\) quyển vở.

a) \(1 - \frac{1}{2} + \frac{1}{3} = \frac{6 - 3 + 2}{6} = \frac{5}{6}\).

b) \(\frac{2}{5} + \frac{3}{5} : \frac{9}{10} = \frac{2}{5} + \frac{3}{5} \cdot \frac{10}{9} = \frac{2}{5} + \frac{2}{3} = \frac{16}{15}\).

c) \(\frac{7}{11} \cdot \frac{3}{4} + \frac{7}{11} \cdot \frac{1}{4} + \frac{4}{11} = \frac{7}{11} \left(\right. \frac{3}{4} + \frac{1}{4} \left.\right) + \frac{4}{11} = \frac{7}{11} + \frac{4}{11} = 1\).

d) \(\left(\right. \frac{3}{4} + 0 , 5 + 25 \% \left.\right) \cdot 2 \frac{2}{3} = \left(\right. \frac{3}{4} + \frac{1}{2} + \frac{1}{4} \left.\right) \cdot \frac{8}{3} = \frac{3}{2} \cdot \frac{8}{3} = 4\).