

Vương Gia Bảo
Giới thiệu về bản thân



































Ta có x2−4x+9=(x−2)2+5⩾5x2−4x+9=(x−2)2+5⩾5.
Suy ra B=1x2−4x+9=1(x−2)2+5⩽15B=x2−4x+91=(x−2)2+51⩽51.
Dấu bằng xảy ra khi x=2x=2.
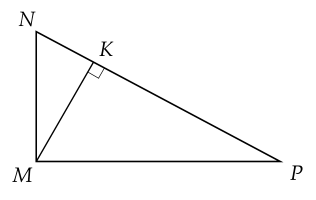
a) Xét ΔKNMΔKNM và ΔMNPΔMNP có:
MKN^=NMP^=90∘MKN=NMP=90∘;
N^N chung;
Suy ra ΔKNM∽ΔMNPΔKNM∽ΔMNP (g.g) (1)
Xét ΔKMPΔKMP và ΔMNPΔMNP có:
MKP^=NMP^=90∘MKP=NMP=90∘
P^P là góc chung
Do đó ΔKMP∽ΔMNPΔKMP∽ΔMNP (g.g) (2)
Từ (1) và (2) suy ra ΔKNM∽ΔKMPΔKNM∽ΔKMP.
b) Theo câu a ΔKNM∽ΔKMPΔKNM∽ΔKMP.
Từ đây ta có tỉ lệ thức: MKKP=NKMKKPMK=MKNK
Nên MK. MK=NK.KPMK. MK=NK.KP hay MK2=NK.KPMK2=NK.KP
c) Từ câu b, ta tính được MK=6MK=6 cm.
Nên SMNP=12MK.NP=12.6.(4+9)=39SMNP=21MK.NP=21.6.(4+9)=39 cm22.
a) Rút gọn A=(x−1)2(x−1)(x+1)=x−1x+1A=(x−1)(x+1)(x−1)2=x+1x−1.
b) Với x=3x=3 thì A=3−13+1=12A=3+13−1=21
Với x=32x=23 thì A=−32−1−32+1=5A=−23+1−23−1=5
c) Ta có biến đối: A=x−1x+1=1+−2x+1A=x+1x−1=1+x+1−2.
Để biểu thức AA nguyên khi −2x+1x+1−2 hay x+1x+1 là ước của −2−2.
Do đó
| x+1x+1 | 11 | −1−1 | 22 | −2−2 |
| xx | 00 | −2−2 | 11 | −3−3 |
Đối chiếu điều kiện ta thấy xx có giá trị −2;−3;0−2;−3;0 thì biểu thức AA nguyên.
Phương trình đã cho trở thành
4x2y2(x2+y2)2−1+x2y2+y2x2−2≥0(x2+y2)24x2y2−1+y2x2+x2y2−2≥0
4x2y2−(x2+y2)2(x2+y2)2+x4+y4−2x2y2x2y2≥0(x2+y2)24x2y2−(x2+y2)2+x2y2x4+y4−2x2y2≥0
−(x2−y2)2(x2+y2)2+(x2−y2)2x2y2≥0(x2+y2)2−(x2−y2)2+x2y2(x2−y2)2≥0
(x2−y2)2.[1x2y2−1(x2+y2)2 ]≥0(x2−y2)2.[x2y21−(x2+y2)21 ]≥0
(x2−y2)2.(x2+y2)2−x2y2x2y2(x2+y2)2≥0(x2−y2)2.x2y2(x2+y2)2(x2+y2)2−x2y2≥0
(x2−y2)2.x4+y4+x2y2x2y2(x2+y2)2≥0(x2−y2)2.x2y2(x2+y2)2x4+y4+x2y2≥0.
Dấu bằng xảy ra khi và chỉ khi x=yx=y hoặc x=−yx=−y.
Gọi xx (km) là quãng đường ABAB.
Điều kiện: x>0x>0.
Thời gian người đó đi xe đạp từ AA đến BB là: x1515x (h);
Thời gian lúc về của người đó là: x1212x (h).
Vì thời gian về nhiều hơn thời gian đi 4545 phút =34=43 (h), nên ta có phương trình:
x12−x15=3412x−15x=43
5x60−4x60=4560605x−604x=6045
5x−4x=455x−4x=45
x=45x=45 (TMĐK)
Vậy quãng đường ABAB dài 4545 (km).
a) A=3x+15x2−9+1x+3−2x−3A=x2−93x+15+x+31−x−32 (với x≠3x=3, x≠−3x=−3)
A=3x+15(x+3)(x−3)+1x+3−2x−3A=(x+3)(x−3)3x+15+x+31−x−32
A=3x+15+x−3−2x−6(x+3)(x−3)A=(x+3)(x−3)3x+15+x−3−2x−6
A=2x+6(x+3)(x−3)A=(x+3)(x−3)2x+6
A=2x−3A=x−32.
b) Để A=23A=32 thì 2x−3=23x−32=32
x−3=3x−3=3
x=6x=6 (thỏa mãn điều kiện).
Vậy x=6x=6 thì A=23A=32.
Từ x−y−z=0⇒ {x−z=y y−x=−z z+y=xx−y−z=0⇒ ⎩⎨⎧x−z=y y−x=−z z+y=x.
B=(1−zx)(1−xy)(1+yz)=x−zz.y−xy.z+yz=yx.−zy.xz=−1B=(1−xz)(1−yx)(1+zy)=zx−z.yy−x.zz+y=xy.y−z.zx=−1
Vậy B=−1B=−1.
Giả sử 1515 người làm cỏ cánh đồng xong trong xx giờ.
Vì số người và thời gian làm là hai đại lượng tỉ lệ nghịch:
Ta có: 10.9=x.1510.9=x.15
Suy ra x=6x=6 giờ.
Vậy 1515 người làm cỏ cánh đồng xong trong 66 giờ.
Giả sử 1515 người làm cỏ cánh đồng xong trong xx giờ.
Vì số người và thời gian làm là hai đại lượng tỉ lệ nghịch:
Ta có: 10.9=x.1510.9=x.15
Suy ra x=6x=6 giờ.
Vậy 1515 người làm cỏ cánh đồng xong trong 66 giờ.
Ba chi đội 7A, 7B, 7C tham gia làm kế hoạch nhỏ thu nhặt giấy vụn tổng cộng được 120120 kg giấy vụn. Tính số giấy mỗi chi đội thu được, biết rằng số giấy mỗi chi đội thu được tỉ lệ với 7;8;97;8;9.
Gọi a,b,ca,b,c lần lượt là số kg giấy vụn của 3 chi đội 7A, 7B, 7C thu nhặt được (0<a,b,c<120)(0<a,b,c<120) Vì số kg giấy vụn của 3 chi đội tỉ lệ với 7;8;97;8;9 và tổng cộng được 120120 kg nên ta có
a7=b8=c97a=8b=9c và a+b+c=120a+b+c=120
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
a7=b8=c9=a+b+c7+8+9=12024=57a=8b=9c=7+8+9a+b+c=24120=5
Suy ra a=35a=35 kg, b=40b=40 kg, c=45c=45 kg.
Vậy số kg giấy vụn của ba lớp 7A, 7B, 7C thu nhặt được lần lượt là 3535 kg; 4040 kg; 4545 kg.