a) Học sinh vẽ hình đúng, ghi đúng GT - KL.

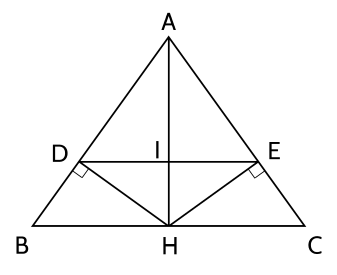
Xét \(\Delta A B D\) và \(\Delta A C H\) có:

\(A H\) là cạnh chung;

\(\hat{B A H} = \hat{C A H}\) (GT)

\(A B = A C\) (GT)

Suy ra \(\Delta A B D = \Delta A C H\) (c.g.c).

b) 

Ta có \(\Delta A B D = \Delta A C H\) (câu a).

\(\Rightarrow \&\text{nbsp}; \hat{A H B} = \hat{A H C}\) (hai góc tương ứng)

Mà \(\hat{A H B} + \hat{A H C} = 18 0^{\circ}\) (hai góc kề bù).

Suy ra \(\hat{A H B} = \hat{A H C} = 9 0^{\circ}\) hay \(A H \bot B C\).

c) Vẽ \(H D \&\text{nbsp}; \bot B C\) với \(D \in A B\); \(H E \&\text{nbsp}; \bot A C\) với \(E \in A C\).

Xét hai tam giác vuông \(\Delta A D H\) và \(\Delta A E H\) có:

\(A H\) là cạnh chung

\(\hat{B A H} = \hat{C A H}\) (GT)

Suy ra \(\Delta A D H = \Delta A E H\) (cạnh huyền - góc nhọn).

Suy ra \(H D = H E\) (hai cạnh tương ứng).

a) Hình vuông với diện tích \(10\) cm\(^{2}\) có độ dài cạnh bằng \(\sqrt{10}\).

Sử dụng MTCT ta tính được \(\sqrt{10} = 3 , 4622...\)

Làm tròn kết quả đến cữ số thập phân thứ hai ta được độ dài cạnh hình vuông cần tính là \(3 , 46\) cm.

b) Uớc lượng số liệu với độ chính xác \(500\) nên phải làm tròn số đến hàng nghìn.

Số dân thành phố uớc tính là \(7\) \(343\) \(000\) người.

a) \(5 , 3.4 , 7 + \left(\right. - 1 , 7 \left.\right) . 5 , 3 - 5 , 9\)

\(= 5 , 3. \left(\right. 4 , 7 - 1 , 7 \left.\right) - 5 , 9\)

\(= 5 , 3.3 - 5 , 9\)

\(= 15 , 9 - 5 , 9 = 10\)

b) \(\frac{2}{3} + \frac{- 1}{3} + \frac{7}{15}\)

\(= \frac{2 + \left(\right. - 1 \left.\right)}{3} + \frac{7}{15}\)

\(= \frac{5 + 7}{15} = \frac{12}{15} = \frac{4}{5}\).

a) Cỡ giày 38;

b) Cỡ giày 36; 40; 42.

(2+31​−0,4)−(7−53​−34​)−(51​+35​−4)

\(= \left(\right. 2 - 7 + 4 - 0 , 4 \left.\right) + \left(\right. \frac{3}{5} - \frac{1}{5} \left.\right) + \left(\right. \frac{1}{3} + \frac{4}{3} - \frac{5}{3} \left.\right)\)

\(= \left(\right. - 1 - 0 , 4 \left.\right) + \frac{2}{5} + 0\)

\(= - 1 - 0 , 4 + 0 , 4 = - 1\).

Thay \(S = 100\) vào \(S = \pi R^{2}\) ta được \(\pi R^{2} = 100\).

Suy ra \(R = \sqrt{\frac{100}{\pi}}\).

Sử dụng MTCT tính được \(R = 5 , 641895835...\)

Cần làm tròn đến hàng phần chục để có độ chính xác \(d = 0 , 05\).

Kết quả là \(R \approx 5 , 6\).

a) Vẽ đúng hình:

Xét \(\Delta A M B\) và \(\Delta A M C\) có:

\(A B = A C\), 

\(\hat{B} = \hat{C}\) (do giả thiết \(\Delta A B C\) cân tại \(A \left.\right)\)

\(M B = M C\) (do giả thiết \(M\) là trung điểm của cạnh \(B C\))

Do đó \(\Delta A M B = \Delta A M C\) (c.g.c).

b) Do giả thiết \(M E \bot A B\), \(\left(\right. E \in A B \left.\right)\);

\(M F \bot A C\), \(\left(\right. F \in A C \left.\right)\) suy ra \(\Delta E M B\) và \(\Delta F M C\) là hai tam giác vuông (ở \(E\) và \(F\)).

Mà \(M B = M C\), \(\hat{B} = \hat{C}\) (chứng minh trong a)).

Do đó \(\Delta E M B = \Delta F M C\) (cạnh huyền-góc nhọn).

Suy ra \(E B = F C\) (cạnh tương ứng).

Mà \(A B = A C\) nên \(E A = A B - E B = A C - F C = F A\).

c) \(\Delta A E F\) cân ở \(A\) (do \(E A = F A\) theo chứng minh trên) nên \(\hat{A E F} = \left(\right. 18 0^{\circ} - \hat{A} \left.\right) : 2\)

Tương tự, \(\Delta A B C\) cân ở \(A\) (giả thiết) nên \(\hat{A B C} = \left(\right. 18 0^{\circ} - \hat{A} \left.\right) : 2\)

Do đó \(\hat{A E F} = \hat{A B C}\), suy ra \(E F\) // \(B C\).

a) Tỉ lệ phần trăm lượng cam tiêu thụ được là \(100 - \left(\right. 20 + 17 , 5 + 35 , 5 \left.\right) = 27 \%\)

b) Do \(35 , 5 > 27 > 20 > 17 , 5\) nên hai loại quả có lượng tiêu thụ nhiều nhất là quýt và cam.

c) Tổng lượng cam và bưởi tiêu thụ được là \(27 + 20 = 47 \%\).

d) \(135\) kg cam bằng \(27 \%\) toàn bộ số quả bán được nên \(100 \%\) số quả bán được là:

     \(135 : 27 \% = 500\) kg.

Giả thiết: Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba.

Kết luận: Chúng song song với nhau.

Cần làm tròn số đến hàng vạn (10  000)

Kết quả làm tròn là số 7 890 000.