Xét \(\Delta A B C\) có \(A B = 10\) cm, \(A C = 17\) cm, \(B C = 21\) cm.

Gọi \(A H\) là đường cao của tam giác.

Vì \(B C\) là cạnh lớn nhất của tam giác nên \(\hat{B} , \hat{C} < 9 0^{\circ}\), do đó \(H\) nằm giữa \(B\) và \(C\).

Đặt \(H C = x , H B = y\), ta có : \(x + y = 21\) (1)

Mặt khác \(\left(A H\right)^{2} = 1 0^{2} - y^{2} , \left(A H\right)^{2} = 1 7^{2} - x^{2}\) nên \(x^{2} - y^{2} = 1 7^{2} - 1 0^{2} = 289 - 100 = 189\) (2)

Từ (1) và (2) suy ra \(x + y = 21\), \(x - y = 9\).

Do đó \(x = 15\), \(y = 6\).

Ta có \(\left(A H\right)^{2} = 1 0^{2} - 6^{2} = 64\) nên \(A H = 8\).

Vậy \(S_{A B C} = \frac{21.8}{2} = 84\) (cm\(^{2}\)).

Chiều cao của mỗi hình chóp tứ giác đều là:

     \(30 : 2 = 15\) (m).

Thể tích của lồng đèn quả trám là:

     \(V = 2. \left(\right. \frac{1}{3} . 20.20.15 \left.\right) = 4 000\) (cm\(^{3}\)).

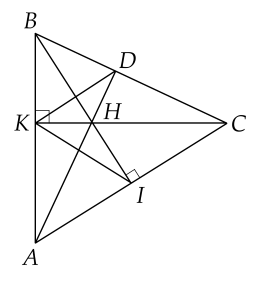
a) Vì tam giác \(K B C\) vuông tại \(K\) suy ra \(\hat{K B H} = 9 0^{\circ}\)

Vì \(C I \bot B I\) (gt) suy ra \(\hat{C l H} = 9 0^{\circ}\)

Xét \(\triangle K B H\) và \(\triangle C H I\) có:

\(\hat{K B H} = \hat{C I H} = 9 0^{\circ}\);

\(\hat{B H K} = \hat{C H I}\) (đối đỉnh)

Suy ra \(\Delta B H K \sim \Delta C H I\) (g.g)

b) Ta có \(\Delta B H K \sim \Delta C H I\) suy ra \(\hat{H B K} = \hat{H C I}\) (hai góc tương ứng) 

Mà \(B H\) là tia phân giác của \(\hat{A B C}\) nên \(\hat{H B K} = \hat{H B C}\).

Do đó \(\hat{H B C} = \hat{H C I}\).

Xét \(\triangle C I B\) và \(\triangle H I C\) có:

\(\hat{C I B}\) chung;

\(\hat{I B C} = \hat{H C I}\) (cmt)

Vậy \(\Delta C I B \approx \Delta H I C\) (g.g) suy ra \(\frac{C I}{H I} = \frac{I B}{I C}\)

Hay \(\left(C I\right)^{2} = H I . I B\)

c) Xét \(\triangle A B C\) có \(B I \bot A C\); \(C K \bot A B\); \(B I \cap C K = \left{\right. H \left.\right}\)

Nên \(H\) là trực tâm \(\triangle A B C\) suy ra \(A H \bot B C\) tại \(D\).

Từ đó ta có \(\triangle B K C \sim \triangle H D C\) (g.g) nên \(\frac{C B}{C H} = \frac{C K}{C D}\)

Suy ra \(\frac{C B}{C K} = \frac{C H}{C D}\) nên \(\triangle B H C \sim \triangle K D C\) (c.g.c)

Khi đó \(\hat{H B C} = \hat{D K C}\) (hai góc tương ứng)

Chứng minh tương tự \(\hat{H A C} = \hat{I K C}\)

Mà \(\hat{H A C} = \hat{H B C}\) (cùng phụ \(\hat{A C B}\) )

Suy ra \(\&\text{nbsp}; \hat{D K C} = \hat{I K C}\).

Vậy \(K C\) là tia phân giác của \(\hat{I K D}\).

Có \(19\) kết quả cho hành động trên.

Có \(8\) kết quả thuận lợi cho biến cố đã cho nên xác suất cho biến cố là: \(\frac{8}{19}\).

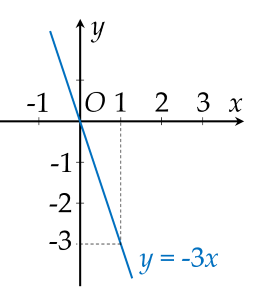
a) Xét đường thẳng: \(\left(\right. d_{1} \left.\right) : y = - 3 x\).

Nếu \(x = 0\) thì \(y = 0\) suy ra \(\left(\right. d_{1} \left.\right)\) đi qua điểm có tọa độ \(\left(\right. 0 ; 0 \left.\right)\)

Nếu \(x = 1\) thì \(y = - 3\) suy ra \(\left(\right. d_{1} \left.\right)\) đi qua điểm có tọa độ \(\left(\right. 1 ; - 3 \left.\right)\)

Ta vẽ đồ thị:

b) Vì \(\left(\right. d_{3} \left.\right) : y = a x + b\) song song với \(\left(\right. d_{2} \left.\right) : y = x + 2\) nên \(a = 1 , b \neq 2\).

Khi đó đường thẳng \(\left(\right. d_{3} \left.\right)\) có dạng \(y = x + b\) với \(b \neq 2\).

Vì \(\left(\right. d_{3} \left.\right)\) đi qua điểm có tọa độ \(A \left(\right. - 1 ; 3 \left.\right)\) nên: \(3 = - 1 + b\) hay \(b = 3 + 1 = 4\) (thỏa mãn).

Vậy đường thẳng \(\left(\right. d_{3} \left.\right)\) là \(\left(\right. d_{3} \left.\right) : y = - x + 4\).

2) Gọi số sản phẩm mà tổ I làm được theo kế hoạch là \(x\).

Điều kiện: \(x \in \mathbb{N}^{*}\); \(x < 900\), đơn vị: sản phẩm.

Số sản phẩm mà tổ II làm được theo kế hoạch là: \(900 - x\) (sản phẩm).

Theo bài ra, do cải tiến kĩ thuật nên tổ một vượt mức \(20 \%\) và tổ hai vượt mức \(15 \%\) so với kế hoạch.

Số sản phẩm mà tổ I làm được theo thực tế là: \(x + x . \&\text{nbsp}; 20 \% = x + 0 , 2 x = 1 , 2 x\) (sản phẩm);

Số sản phẩm mà tổ II làm được theo thực tế là: \(900 - x + \left(\right. 900 - x \left.\right) . 15 \% = 1 035 - 1 , 15 x\) (sản phẩm).

Vì thực tế hai tổ đã sản xuất được \(1 055\) sản phẩm nên ta có phương trình: \(1 , 2 x + 1 035 - 1 , 15 x = 1 055\)

Giải phương trình tìm được \(x = 400\) (sản phẩm)

Khi đó, số sản phẩm mà tổ II làm được theo kế hoạch là: \(900 - 400 = 500\) (sản phẩm).

Vậy theo kế hoạch tổ I làm được \(400\) sản phẩm, tổ II làm được \(500\) sản phẩm.

a) \(2 x = 7 + x\)

\(2 x - x = 7\)

\(x = 7\).

Phương trình đã cho có nghiệm \(x = 7\).

b) \(\frac{x - 3}{5} + \frac{1 + 2 x}{3} = 6\)

\(\frac{3 \left(\right. x - 3 \left.\right)}{15} + \frac{5. \left(\right. 1 + 2 x \left.\right)}{15} = 6\)

\(3 x - 9 + 5 + 10 x = 90\)

\(13 x = 94\)

\(x = \frac{94}{13}\).

Phương trình đã cho có nghiệm \(x = \frac{94}{13}\).

a) Ở mỗi mặt, có \(4\) hình lập phương nhỏ được sơn một mặt (các hình được gạch sọc).

Ở sáu mặt có: \(4.6 \&\text{nbsp}; = 24\) (hình).

b) Ở mỗi cạnh, có \(2\) hình lập phương được sơn hai mặt (các hình ghi dấu "\(x\)").

Ở \(12\) cạnh có : \(2.12 = 24\) (hình).

Bài 1

Bài 1. (1 điểm) Giải các phương trình sau:

a) \(3 x - 4 = 5 + x\).

b) \(3 \left(\right. x - 1 \left.\right) - 7 = 5 \left(\right. x + 2 \left.\right)\). 

Hướng dẫn giải:

a. Ta có: \(3 x - 4 = 5 + x\)

\(3 x - x = 5 + 4\)

\(2 x = 9\)

\(x = \frac{9}{2}\).

Vậy phương trình đã cho có nghiệm \(x = \frac{9}{2}\).

b. Ta có: \(3 \left(\right. x - 1 \left.\right) - 7 = 5 \left(\right. x + 2 \left.\right)\)

\(3 x - 3 - 7 = 5 x + 10\)

\(5 x - 3 x = - 3 - 7 - 10\)

\(2 x = - 20\)

\(x = - 10\).

Vậy phương trình có nghiệm \(x = - 10\).

a. Ta có: \(3 x - 4 = 5 + x\)

\(3 x - x = 5 + 4\)

\(2 x = 9\)

\(x = \frac{9}{2}\).

Vậy phương trình đã cho có nghiệm \(x = \frac{9}{2}\).

b. Ta có: \(3 \left(\right. x - 1 \left.\right) - 7 = 5 \left(\right. x + 2 \left.\right)\)

\(3 x - 3 - 7 = 5 x + 10\)

\(5 x - 3 x = - 3 - 7 - 10\)

\(2 x = - 20\)

\(x = - 10\).

Vậy phương trình có nghiệm \(x = - 10\).

Bài 2

Bài 2. (1,5 điểm) Một ca nô đi xuôi khúc sông từ \(A\) đến \(B\) hết \(1\) giờ \(30\) phút và đi ngược từ \(B\) về \(A\) hết \(2\) giờ. Biết vận tốc dòng nước là \(3\) km/h. Tính vận tốc riêng của ca nô và chiều dài quãng sông \(A B\)?

Hướng dẫn giải:

Gọi vận tốc riêng của ca nô là \(x\) (km/h, \(x > 3\)).

Vận tốc ca nô khi đi xuôi khúc sông từ \(A\) đến \(B\) là: \(x + 3\) (km/h);

Vận tốc ca nô khi đi ngược khúc sông từ \(B\) về \(A\) là: \(x - 3\) (km/h);

Khúc sông \(A B\) có chiều dài không đổi nên ta có phương trình: \(\frac{3}{2} \left(\right. x + 3 \left.\right) = 2 \left(\right. x - 3 \left.\right)\).

Giải phương trình trên ta nhận được \(x = 21\) (thỏa mãn)

Do đó vận tốc riêng của ca nô là \(21\) km/h.

Chiều dài khúc sông là: \(2 \left(\right. 21 - 3 \left.\right) = 36\) (km).

Vậy vận tốc riêng của cano là \(21\) km/h, chiều dài khúc sông là \(36\) km .

Gọi vận tốc riêng của ca nô là \(x\) (km/h, \(x > 3\)).

Vận tốc ca nô khi đi xuôi khúc sông từ \(A\) đến \(B\) là: \(x + 3\) (km/h);

Vận tốc ca nô khi đi ngược khúc sông từ \(B\) về \(A\) là: \(x - 3\) (km/h);

Khúc sông \(A B\) có chiều dài không đổi nên ta có phương trình: \(\frac{3}{2} \left(\right. x + 3 \left.\right) = 2 \left(\right. x - 3 \left.\right)\).

Giải phương trình trên ta nhận được \(x = 21\) (thỏa mãn)

Do đó vận tốc riêng của ca nô là \(21\) km/h.

Chiều dài khúc sông là: \(2 \left(\right. 21 - 3 \left.\right) = 36\) (km).

Vậy vận tốc riêng của cano là \(21\) km/h, chiều dài khúc sông là \(36\) km .

Bài 3

Bài 3. (1,0 điểm) Trong một hộp có \(20\) thẻ gồm \(4\) thẻ được đánh số 1, \(4\) thẻ được đánh số 2, \(6\) thẻ được đánh số 3, \(3\) thẻ được đánh số 4 và \(3\) thẻ được đánh số 5. Tính xác suất cho biến cố “Thẻ rút ra là thẻ đánh số 3”.

Hướng dẫn giải:

Xác suất cho biến cố "Thẻ rút ra là thẻ đánh số 3" là: \(\frac{6}{20} = \frac{3}{10}\).

Xác suất cho biến cố "Thẻ rút ra là thẻ đánh số 3" là: \(\frac{6}{20} = \frac{3}{10}\).

Bài 4

Bài 4. (2,5 điểm) Cho \(\Delta A B C\) nhọn, đường cao \(A H\). Kẻ \(H E \bot A B \left(\right. E \in A B \left.\right) , H F \bot A C \left(\right. F \in A C \left.\right)\).

a) Chứng minh \(\Delta A E H \sim \Delta A H B\) từ đó suy ra \(A H^{2} = A E . A B\)

b) Chứng minh \(A E . A B = A F . A C\)

c) Cho chu vi các \(\Delta A E F\) và \(\Delta A C B\) lần lượt là \(20\) cm và \(30\) cm. Tính diện tích \(\Delta A E F\) và \(\Delta A C B\) biết diện tích \(\Delta A C B\) lớn hơn diện tích \(\Delta A E F\) là \(25\) cm\(^{2}\).

Hướng dẫn giải:

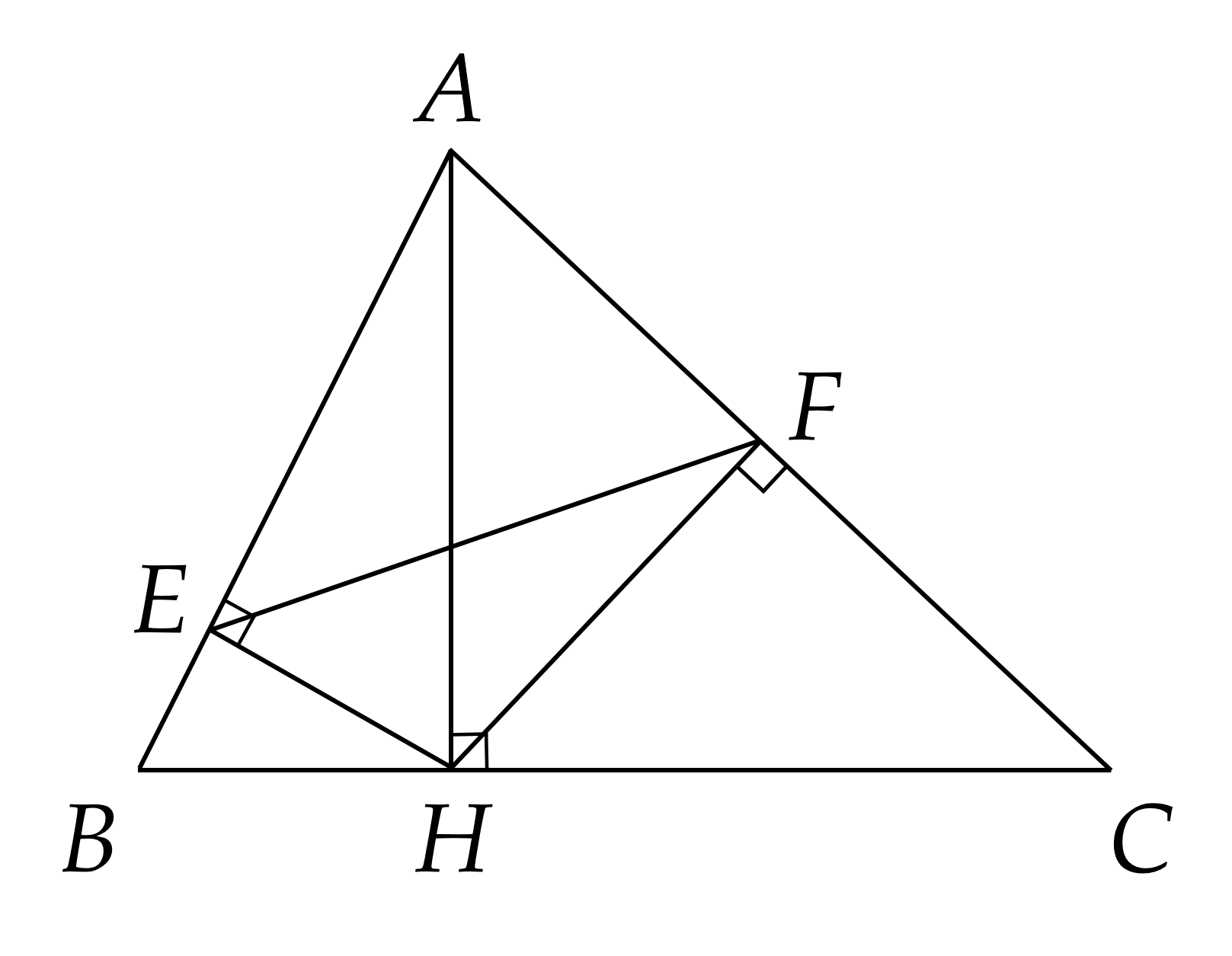
a) Xét \(\Delta A E H\) và \(\Delta A H B\) có:

\(\hat{B A H}\) chung và \(\hat{A E H} = \hat{A H B} = 9 0^{\circ}\)

Do đó \(\Delta A E H \sim \Delta A H B\) (g.g)

Suy ra \(\frac{A H}{A B} = \frac{A E}{A H}\) hay \(A H^{2} = A E . A B\) (1)

b) Chứng minh tương tự \(\Delta A H F \sim \Delta A C H\) (g.g) 

Suy ra \(\frac{A H}{A C} = \frac{A F}{A H}\) hay \(A H^{2} = A F . A C\) (2)

Từ (1) và (2) suy ra \(A E . A B = A F . A C\)

c) Ta có \(A E . A B = A F . A C\) nên \(\frac{A E}{A C} = \frac{A F}{A B}\).

Xét \(\Delta A E F\) và \(\Delta A C B\) có:

\(\hat{E A F}\) chung

\(\frac{A E}{A C} = \frac{A F}{A B}\) (cmt)

Do đó \(\Delta A E F \&\text{nbsp}; \sim \Delta A C B\) (c.g.c).

Suy ra \(\frac{E F}{C B} = \frac{P_{A E F}}{P_{A C B}} = \frac{20}{30} = \frac{2}{3}\) (tỉ số chu vi bằng tỉ số đồng dạng)

Áp dụng tính chất dãy tỉ số bằng nhau ta có \(\frac{S_{A E F}}{4} = \frac{S_{A C B}}{9} = \frac{S_{A C B} - S_{A E F}}{9 - 4} = \frac{25}{5} = 5\)

Suy ra

\(S_{A E F} = 5.4 = 20\) cm\(^{2}\);

\(S_{A C B} = 5.9 = 45\) cm\(^{2}\).

Vậy \(S_{A E F} = 20\) cm\(^{2}\) và \(S_{A C B} = 45\) cm\(^{2}\).

a) Xét \(\Delta A E H\) và \(\Delta A H B\) có:

\(\hat{B A H}\) chung và \(\hat{A E H} = \hat{A H B} = 9 0^{\circ}\)

Do đó \(\Delta A E H sim \Delta A H B\) (g.g)

Suy ra \(\frac{A H}{A B} = \frac{A E}{A H}\) hay \(A H^{2} = A E . A B\) (1)

b) Chứng minh tương tự \(\Delta A H F sim \Delta A C H\) (g.g) 

Suy ra \(\frac{A H}{A C} = \frac{A F}{A H}\) hay \(A H^{2} = A F . A C\) (2)

Từ (1) và (2) suy ra \(A E . A B = A F . A C\)

c) Ta có \(A E . A B = A F . A C\) nên \(\frac{A E}{A C} = \frac{A F}{A B}\).

Xét \(\Delta A E F\) và \(\Delta A C B\) có:

\(\hat{E A F}\) chung

\(\frac{A E}{A C} = \frac{A F}{A B}\) (cmt)

Do đó \(\Delta A E F \& \text{nbsp} ; sim \Delta A C B\) (c.g.c).

Suy ra \(\frac{E F}{C B} = \frac{P_{A E F}}{P_{A C B}} = \frac{20}{30} = \frac{2}{3}\) (tỉ số chu vi bằng tỉ số đồng dạng)

Áp dụng tính chất dãy tỉ số bằng nhau ta có \(\frac{S_{A E F}}{4} = \frac{S_{A C B}}{9} = \frac{S_{A C B} - S_{A E F}}{9 - 4} = \frac{25}{5} = 5\)

Suy ra

\(S_{A E F} = 5.4 = 20\) cm\(^{2}\);

\(S_{A C B} = 5.9 = 45\) cm\(^{2}\).

Vậy \(S_{A E F} = 20\) cm\(^{2}\) và \(S_{A C B} = 45\) cm\(^{2}\).

Bài 5

Bài 5. (1,0 điểm) Cho tam giác \(A B C\), trung tuyến \(A M\), đường phân giác của góc \(A M B\) cắt \(A B\) tại \(D\). Cho \(B C = 30\) cm; \(A D = 6\) cm; \(A B = 10\) cm. Tính độ dài \(A M\). 

Hướng dẫn giải:

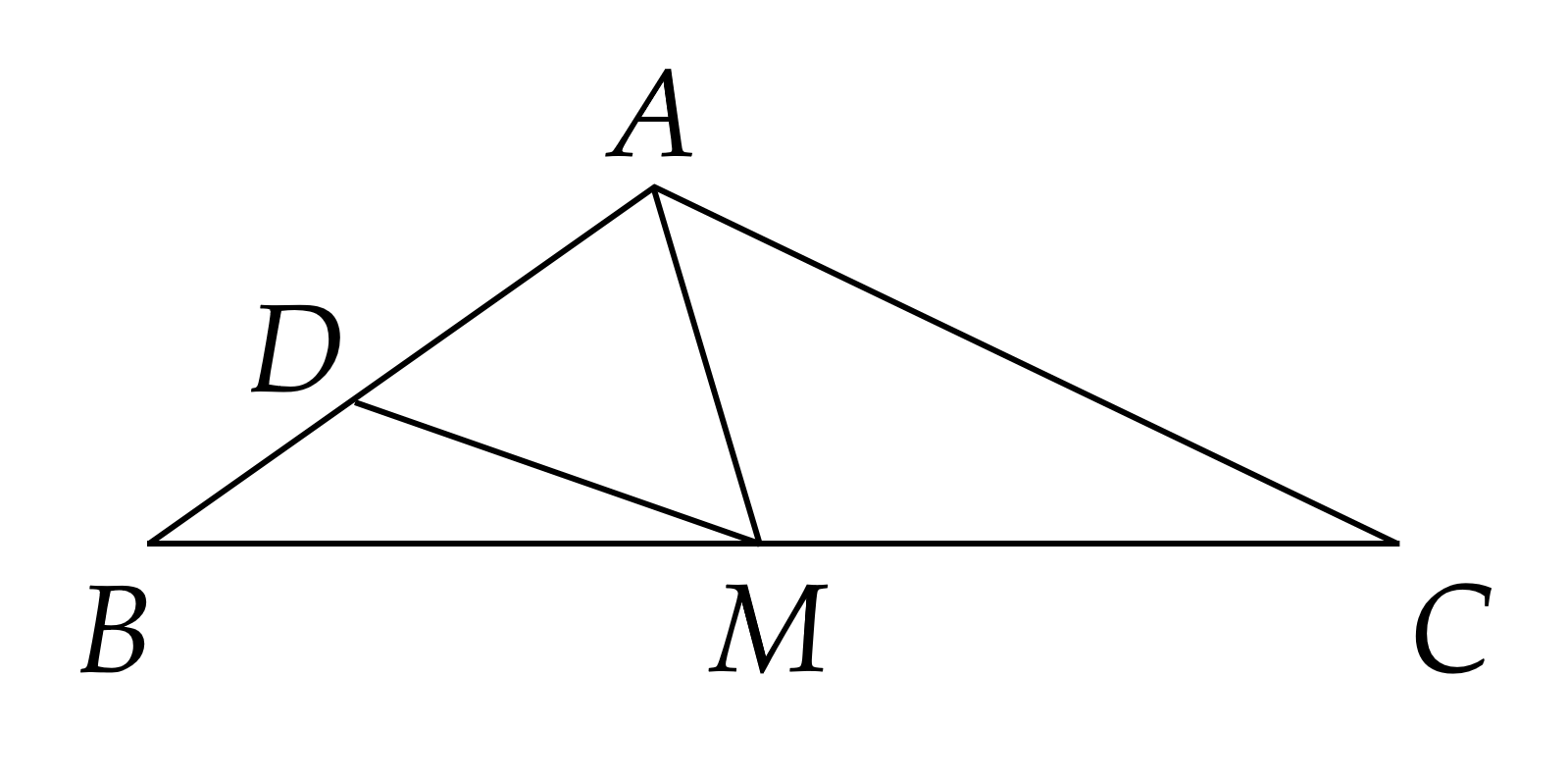
Ta có: \(A B = A D + D B\)

Suy ra \(D B = A B - A D = 10 - 6 = 4\) cm

\(A M\) là trung tuyến của \(\Delta A B C\) suy ra \(M\) là trung điểm của \(B C\)

Suy ra \(B M = C M = \frac{1}{2} B C = 15\) cm.

 Xét \(\Delta A B M\) có \(M D\) là phân giác của góc \(A M B\) nên

\(\frac{A M}{B M} = \frac{A D}{D B}\)

\(\frac{A M}{B M} = \frac{6}{4} = \frac{3}{2}\)

Do đó \(A M = \frac{3}{2} . B M = \frac{3}{2} . 15 = 22 , 5\) (cm).

a) Xét \(\Delta A E H\) và \(\Delta A H B\) có:

\(\hat{B A H}\) chung và \(\hat{A E H} = \hat{A H B} = 9 0^{\circ}\)

Do đó \(\Delta A E H \sim \Delta A H B\) (g.g)

Suy ra \(\frac{A H}{A B} = \frac{A E}{A H}\) hay \(A H^{2} = A E . A B\) (1)

b) Chứng minh tương tự \(\Delta A H F \sim \Delta A C H\) (g.g) 

Suy ra \(\frac{A H}{A C} = \frac{A F}{A H}\) hay \(A H^{2} = A F . A C\) (2)

Từ (1) và (2) suy ra \(A E . A B = A F . A C\)

c) Ta có \(A E . A B = A F . A C\) nên \(\frac{A E}{A C} = \frac{A F}{A B}\).

Xét \(\Delta A E F\) và \(\Delta A C B\) có:

\(\hat{E A F}\) chung

\(\frac{A E}{A C} = \frac{A F}{A B}\) (cmt)

Do đó \(\Delta A E F \&\text{nbsp}; \sim \Delta A C B\) (c.g.c).

Suy ra \(\frac{E F}{C B} = \frac{P_{A E F}}{P_{A C B}} = \frac{20}{30} = \frac{2}{3}\) (tỉ số chu vi bằng tỉ số đồng dạng)

Áp dụng tính chất dãy tỉ số bằng nhau ta có \(\frac{S_{A E F}}{4} = \frac{S_{A C B}}{9} = \frac{S_{A C B} - S_{A E F}}{9 - 4} = \frac{25}{5} = 5\)

Suy ra

\(S_{A E F} = 5.4 = 20\) cm\(^{2}\);

\(S_{A C B} = 5.9 = 45\) cm\(^{2}\).

Vậy \(S_{A E F} = 20\) cm\(^{2}\) và \(S_{A C B} = 45\) cm\(^{2}\).

Xác suất cho biến cố "Thẻ rút ra là thẻ đánh số 3" là: \(\frac{6}{20} = \frac{3}{10}\).