a) Diện tích đáy hình vuông của chiếc lều là:

     \(_{\overset{}{}}3^2=9\) (m\(^{2}\)) 

Thể tích không khí bên trong chiếc lều là:

    \(\frac{1}{3}.9.2,8=8,4\) (m\(^{3}\))

b) Diện tích xung quanh của chiếc lều là:

     \(\frac{1}{2}.4.3.3,18=19,08\) (m\(^{2}\))

Diện tích vải phủ bốn phía và trải nền đất cho chiếc lều là:

     \(9+19,08=28,08\) (m\(^{2}\)).

Do \(28 , 08 > 20\) nên số tiền mua vải được giảm giá \(5 \%\) trên tổng hóa đơn.

Vậy số tiền mua vải là:

     \(28 , 08.15 000. \left(\right. 100 \% - 5 \% \left.\right) = 400 140\) (đồng).​

a) Xét tứ giác ABCD ta có:

\(\hat{A} + \hat{B} + \hat{C} + \hat{D} = 36 0^{o}\)

\(\Rightarrow \hat{D} = 36 0^{o} - 10 2^{o} - 10 2^{o} - 10 2^{o}\)

\(\Rightarrow \hat{D} = 5 4^{o}\) 

b) Xét tam giác vuông AOD ta có:

\(A D^{2} = O D^{2} + O A^{2}\)

\(\Rightarrow O A = \sqrt{A D^{2} - O D^{2}}\)

\(\Rightarrow O A = \sqrt{3 0^{2} - 26 , 7^{2}} \approx 13 , 7 \left(\right. c m \left.\right)\)

Xét tam giác vuông AOB ta có:

\(A B^{2} = O A^{2} + O B^{2}\)

\(\Rightarrow O B = \sqrt{A B^{2} - O A^{2}}\)

\(\Rightarrow O B = \sqrt{17 , 5^{2} - 13 , 7^{2}} \approx 10 , 9 \left(\right. c m \left.\right)\)

Độ dài đường chéo BD là:

\(B D = O B + O D = 26 , 7 + 10 , 9 \approx 37 , 6 \left(\right. c m \left.\right)\)

a) \(x y + y^{2} - x - y\)

\(= \left(\right. x y + y^{2} \left.\right) - \left(\right. x + y \left.\right)\)

\(= y \left(\right. x + y \left.\right) - \left(\right. x + y \left.\right)\)

\(=\left(\right.x+y\left.\right)\left(\right.y-1\left.\right)\)

b) \(\left(\right.x^2y^2-8\left.\right)^2-1\)

\(= \left(\right. x^{2} y^{2} - 8 - 1 \left.\right) \left(\right. x^{2} y^{2} - 8 + 1 \left.\right)\)

\(= \left(\right. x^{2} y^{2} - 9 \left.\right) \left(\right. x^{2} y^{2} - 7 \left.\right)\)

\(=\left(\right.xy-3\left.\right)\left(\right.xy+3\left.\right)\left(\right.x^2y^2-7\left.\right)\)

\(=\left(\right.x-1\left.\right)\left(\right.x+8\left.\right)\)

a) \(\left(\right. - 12 x^{13} y^{15} + 6 x^{10} y^{14} \left.\right) : \left(\right. - 3 x^{10} y^{14} \left.\right)\)

\(= \left(\right. - 12 x^{13} y^{15} \left.\right) : \left(\right. - 3 x^{10} y^{14} \left.\right) + \left(\right. 6 x^{10} y^{14} \left.\right) : \left(\right. - 3 x^{10} y^{14} \left.\right)\)

\(=4x^3y-1\)

b) \(\left(\right. x - y \left.\right) \left(\right. x^{2} - 2 x + y \left.\right) - x^{3} + x^{2} y\)

\(= x \left(\right. x^{2} - 2 x + y \left.\right) - y \left(\right. x^{2} - 2 x + y \left.\right) - x^{3} + x^{2} y\)

\(= x^{3} - 2 x^{2} + x y - x^{2} y + 2 x y - y^{2} - x^{3} + x^{2} y\)

\(= - 2 x^{2} + 3 x y - y^{2} .\)

Đám mây hã:)))

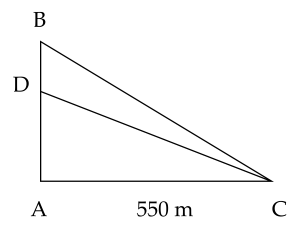
Gọi vị trí đặt loa là \(D\) suy ra \(D\) nằm giữa \(A\) và \(B\).Trong tam giác vuông \(A D C\) ta có \(D C\) là cạnh lớn nhất (đối diện với góc lớn nhất) nên \(D C > A C = 550\) m. Vậy tại \(C\) không thể nghe tiếng loa, do vị trí \(C\) đã nằm ngoài bán kính phát sóng của loa.

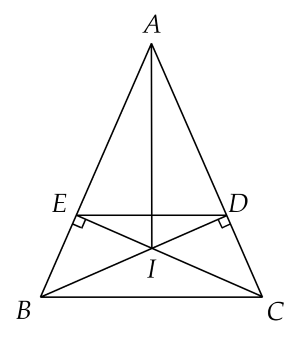
a) Xét \(\Delta D A B\) và \(\Delta E A C\) lần lượt vuông tại \(D\) và \(E\) có:

   \(A B = A C\) (\(\Delta A B C\) cân tại \(A\));

   \(\hat{B A C}\) chung.

Suy ra \(\Delta D A B = \Delta E A C\) (cạnh huyền, góc nhọn)

Suy ra \(A D = A E\) (hai cạnh tương ứng).

b) Xét \(\Delta E A I\) và \(\Delta D A I\) lần lượt vuông tại \(E\) và \(D\):

    \(A E \&\text{nbsp}; = A D\)

    Chung cạnh \(A I .\)

Suy ra \(\Delta E A I = \Delta D A I\) (cạnh huyền, cạnh góc vuông).

Suy ra \(\&\text{nbsp}; \hat{E A I} = \hat{D A I}\) (hai góc tương ứng).

Suy ra \(A I\) là tia phân giác của \(\hat{B A C}\).

c) Có \(A D = A E\) suy ra \(\Delta A E D\) cân tại \(A\).

Suy ra \(\hat{A E D} = \frac{18 0^{\circ} - \hat{B A C}}{2}\)

Tam giác \(A B C\) cân tại \(A\), suy ra \(\hat{A B C} = \frac{18 0^{\circ} - \hat{B A C}}{2}\).

Từ \(\left(\right. 1 \left.\right)\) và \(\left(\right. 2 \left.\right)\) suy ra \(\hat{A E D} = \hat{A B C}\) (hai góc ở vị trí đồng vị) nên \(E D\) // \(B C\).

Nghiệm của đa thức \(P \left(\right. x \left.\right) = 5 x + 3\) là \(x = \frac{- 3}{5}\).

a) Tổng số lượng nhập khẩu phân bón các loại của nước ta trong giai đoạn từ năm 2017 đến năm 2020 là:

\(4 727 , 3 + 4 227 , 5 + 3 799 , 2 + 3 803 , 4 = 16 557 , 4\) (nghìn tấn)

b) Số % nhập khẩu phân bón các loại năm 2019 giảm so với năm 2018 là:

\(\frac{\left(\right. 4 227 , 5 - 3 799 , 2 \left.\right) . 100 \%}{4 227 , 5} = \frac{428 , 3.100 \%}{4 227 , 5} \approx 10 , 1 \%\)

c) Giá trị nhập khẩu phân bón các loại năm 2017 gấp giá trị nhập khẩu phân bón các loại năm 2020 số lần là:

\(\frac{1 253 , 1}{951 , 5} \approx 1 , 3\) (lần)