Do \(A\) là trung điểm \(O B\), nên \(O B = 2. O A\).

Thay số \(O A = 2\) cm, ta có

\(O B = 2.2 = 4\) (cm)

2.

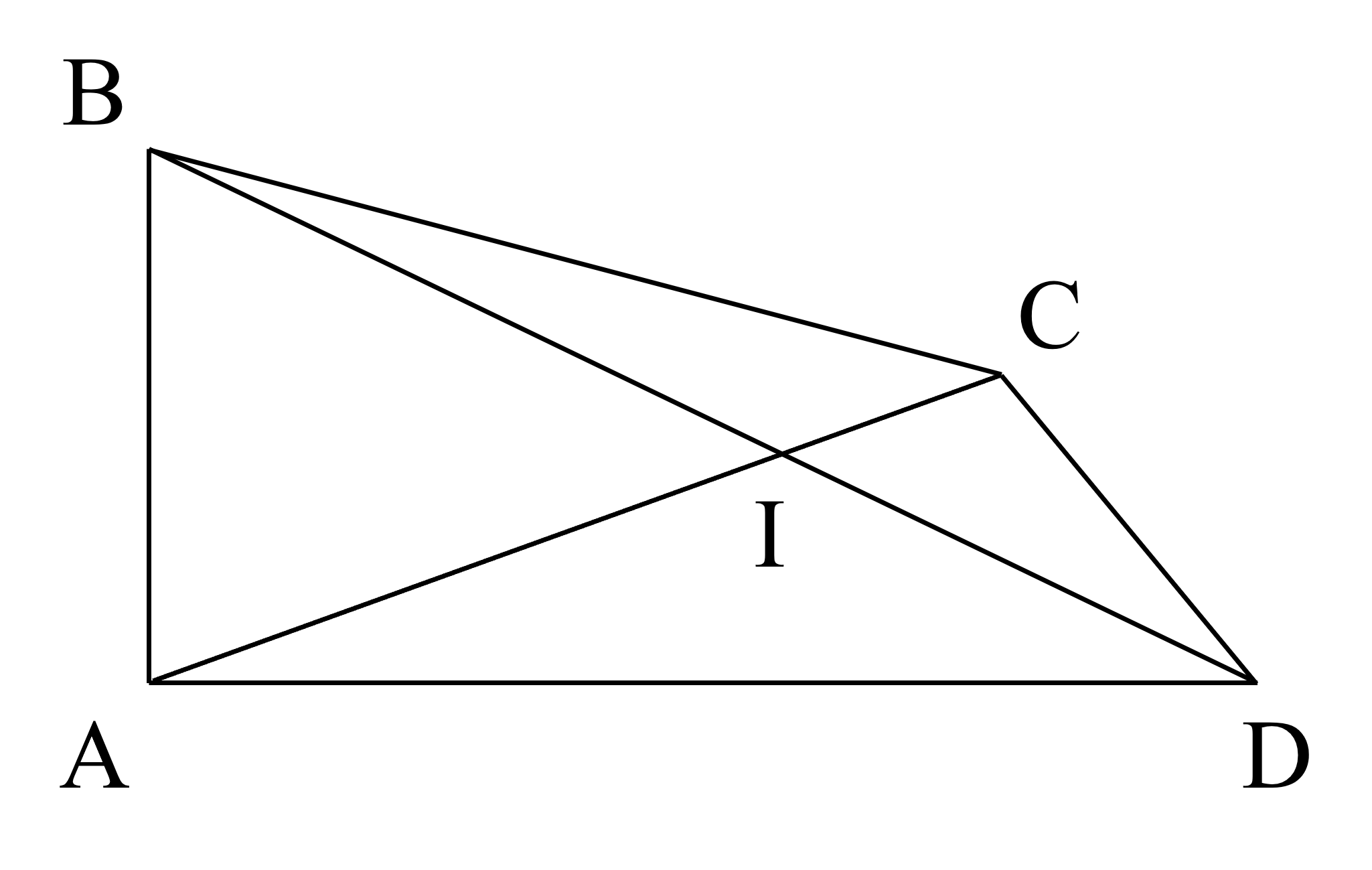
a) Điểm \(C\) và điểm \(I\) nằm trong góc \(B A D\).

b) (Học sinh nêu ra một góc bẹt sẽ đạt điểm tối đa phần này.)

Các góc bẹt trong hình là góc \(B I D\) và \(A I C\).

c) (Không trừ điểm học sinh khi đo góc có sai số từ \(1^{\circ}\) đến \(2^{\circ}\)).

Đo góc, ta lần lượt có các số đo góc như sau:

\(\hat{A I C} = 18 0^{\circ}\)

\(\hat{A C D} = 7 0^{\circ}\)

\(\hat{B C D} = 13 5^{\circ}\)

\(\hat{B A D} = 9 0^{\circ}\)

Sắp xếp các góc theo thứ tự tăng dần về số đo, ta được:

\(\hat{A C D} ; \hat{B A D} ; \hat{B C D} ; \hat{A I C}\).

Số học sinh đạt loại Tốt là:

\(45. \frac{4}{15} = 12\) (học sinh)

Số học sinh đạt loại Khá là:

\(12. \frac{5}{3} = 20\) (học sinh)

Số học sinh được xếp loại Đạt là:

\(45 - 12 - 20 = 13\) (học sinh)

Đáp Số 12 học sinh

a) \(\frac{1}{2} - \frac{1}{2} : x = \frac{3}{4}\)

\(\frac{1}{2} : x = \frac{1}{2} - \frac{3}{4}\)

\(\frac{1}{2} : x = \frac{- 1}{4}\)

\(x = \frac{1}{2} : \&\text{nbsp}; \frac{- 1}{4}\)

\(x = - 2\)

b) \(\frac{x - 1}{15} = \frac{3}{5}\)

\(\frac{x - 1}{15} = \frac{9}{15}\)

\(x - 1 = 9\)

\(x = 10\)

c) \(x + 2 , 5 = 1 , 4\)

\(x = 1 , 4 - 2 , 5\)

\(x = - 1 , 1\)

\(65\)

\(= \left(\right. 2 , 34 + 7 , 66 \left.\right) + \left(\right. 4 , 65 + 5 , 35 \left.\right)\)

\(= 10 + 10\)

\(= 20\)

b) \(B = 2 , 13.75 + 2 , 13.25\)

\(= 2 , 13. \left(\right. 75 + 25 \left.\right)\)

\(= 2 , 13.100\)

\(= 213\)

c) \(C = \frac{1}{3} - \frac{1}{3} : \frac{3}{4}\)

\(= \frac{1}{3} - \frac{1}{3} . \&\text{nbsp}; \frac{4}{3}\)

\(= \frac{1}{3} - \frac{4}{9}\)

\(= \frac{3}{9} - \frac{4}{9}\)

\(= \frac{- 1}{9}\)

A