

Nguyễn Phương Linh
Giới thiệu về bản thân



































Gọi số luống rau trong vườn nhà Mai là xx (x∈N,x>5x∈N,x>5)
Gọi số cây rau trồng trên mỗi luống là yy (y∈N,y>2y∈N,y>2)
Tổng số cây rau bắp cải trong vườn nhà Mai là xyxy
Theo bài ra ta có hệ phương trình { xy−(x+7)(y−2)=9 (x−5)(y+2)−xy=15{ xy−(x+7)(y−2)=9(x−5)(y+2)−xy=15
⇔{ 2x−7y=−5 2x−5y=25⇔{ 2x−7y=−52x−5y=25
Giải hệ phương trình tìm được { x=50 y=15{ x=50y=15 (thoả mãn điều kiện của ẩn)
Vậy tổng số cây rau bắp cải trong vườn nhà Mai là 50.15=75050.15=750 cây.
Gọi vị trí ban đầu của người đó là điểm AA.
Vì thời gian thực hiện mỗi vòng của đu quay là 3030 phút nên khi đu quay quay đều thì 1010 phút người đó đi được 1331 vòng tròn và đang ở vị trí điểm BB như hình vẽ sau:
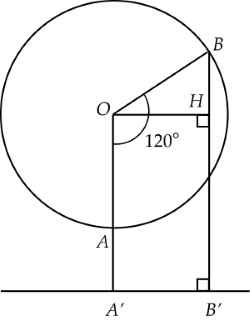
Gọi A′,B′A′,B′ lần lượt là hình chiếu của A,BA,B trên mặt đất, kẻ OH⊥BB′OH⊥BB′.Ta có: AOB^=13.360∘=120∘, OA′=80AOB=31.360∘=120∘, OA′=80 m.
Vì OA′B′HOA′B′H là hình chữ nhật (tứ giác có ba góc vuông) nên HB′=OA′=80HB′=OA′=80 (m).
Ta có: AOH^=90∘AOH=90∘
BOH^=120∘−90∘=30∘BOH=120∘−90∘=30∘
Xét tam giác vuông OBHOBH có:
BH=OB.sin30∘=75.12=37,5BH=OB.sin30∘=75.21=37,5 (m)
BB′=BH+HB′=37,5+80=117,5BB′=BH+HB′=37,5+80=117,5 (m).
Vậy sau 1010 phút người đó ở độ cao 117,5117,5 m so với mặt đất.
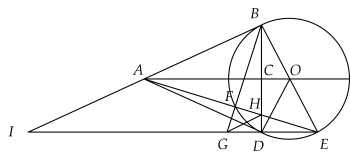
a) Ta có: OB=OD(= R)OB=OD(= R) nên ΔODBΔODB cân tại OO.
Mà OCOC là đường cao của ΔODBΔODB.
Nên OCOC cũng là đường phân giác của ΔODBΔODB.
Suy ra BOC^=COD^BOC=COD hay BOA^=AOD^BOA=AOD.
Xét ΔABOΔABO và ΔADOΔADO có:
OB=OD(=R)OB=OD(=R)
BOA^=AOD^BOA=AOD (chứng minh trên)
Cạnh OAOA chung
Do đó ΔABO=ΔADOΔABO=ΔADO (c-g-c)
Suy ra ABO^=ADO^=90∘ABO=ADO=90∘.
Do đó ADAD là tiếp tuyến của (O)(O).
Ta có: DEB^=12 sđBD⌢ (1)DEB=21 sđBD⌢ (1)
Lại có: BOD^=sđBD⌢BOD=sđBD⌢
Mà BOA^ = 12BOD^BOA = 21BOD
Nên BOA^ = 12 sđBD⌢ (2)BOA = 21 sđBD⌢ (2)
Từ (1)(1) và (2)(2) suy ra BOA^=DEO^BOA=DEO.
Mà hai góc này nằm ở vị trí đồng vị nên OA//DEOA//DE.
b) Vì FF thuộc đường tròn đường kính BEBE nên BFE^=90∘BFE=90∘
Xét ΔABEΔABE vuông tại BB có: BFBF là đường cao
Suy ra AE.AF=AB2AE.AF=AB2
Chứng minh tương tự, ta có: AC.AO=AD2.AC.AO=AD2.
Mà AB=ADAB=AD (tính chất hai tiếp tuyến cắt nhau)
Do đó AB2 =AD2AB2 =AD2
Suy ra: AE.AF=AC.AOAE.AF=AC.AO.
c) Vì DD thuộc đường tròn đường kính BE nên BDE^=90∘BDE=90∘.
Ta có: BDBD là đường cao của ΔBGEΔBGE; EFEF là đường cao của ΔBGEΔBGE.
Mà BD,EFBD,EF cắt nhau tại HH.
Do đó HH là trực tâm của ΔBGEΔBGE.
Suy ra: GH ⊥ BE; AB ⊥ BEGH ⊥ BE; AB ⊥ BE
Nên GH//ABGH//AB.
Xét ΔBIEΔBIEcó: BO=EO(=R);AO//EI(AO//DE)BO=EO(=R);AO//EI(AO//DE).
Do đó AB=AIAB=AI.
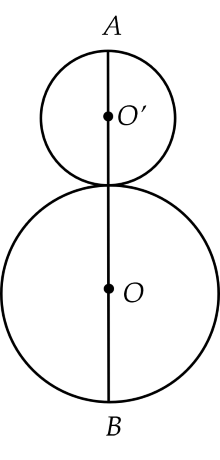
Ta có: 1,81,8 m=180=180 cm
Gọi rr (cm) là bán kính của đường tròn nhỏ
Đường kính của đường tròn nhỏ là 2r2r (cm) (r>0)(r>0)
Đường kính của đường tròn lớn là: 2.2r=4r2.2r=4r (cm)
Ta có: 2r+4r=1802r+4r=180 (vì (O)(O) tiếp xúc với (O’)(O’))
6r=1806r=180
r=30r=30 cm.
Vậy để đắp người tuyết có chiều cao là 1,81,8 m thì ta cần đắp hai quả cầu tuyết có đường kính lần lượt là 6060 cm và 120120 cm.
1.
Ta có:
{ 2x+3y=−2 4x+y=1{ 2x+3y=−24x+y=1
{ 4x+6y=−4 4x+y=1{ 4x+6y=−44x+y=1
{ 5y=−5 4x+y=1{ 5y=−54x+y=1
{ y=−1 4x−1=1{ y=−14x−1=1
{y=−14x=1+1{y=−14x=1+1
{x=12 y=−1⎩⎨⎧ x=21y=−1
Vậy hệ phương trình có nghiệm (x;y)=(12;−1)(x;y)=(21;−1).
2.
a) Với x>0;x≠4x>0;x=4 ta có:
P=(xxx−4x−63x−6+1x+2):( x–2+10−xx+2)P=(xx−4xx−3x−66+x+21):( x–2+x+210−x)
=[xx(x−4)−63(x−2)−1x+2]:(x−4+10−xx+2)=[x(x−4)x−3(x−2)6−x+21]:(x+2x−4+10−x)
=[x(x−2)(x+2)−2x−2+1x+2]:6x+2=[(x−2)(x+2)x−x−22+x+21]:x+26
=x−2(x+2)+x−2(x−2)(x+2):6x+2=(x−2)(x+2)x−2(x+2)+x−2:x+26
=x−2x−4+x−2(x−2)(x+2):6x+2=(x−2)(x+2)x−2x−4+x−2:x+26
=−6(x−2)(x+2).x+26=(x−2)(x+2)−6.6x+2
=−1x−2=x−2−1.
Vậy P=−1x−2P=x−2−1.
b) Với x>0;x≠4x>0;x=4. Ta có
Q=(−x−1).P=(−x−1).−1x−2=x+1x−2=1+3x−2Q=(−x−1).P=(−x−1).x−2−1=x−2x+1=1+x−23.
+ Nếu xx không là số chính phương, suy ra xx là số vô tỉ.
Do đó QQ không nguyên.
+ Nếu xx là số chính phương, suy ra xx là số nguyên.
Do đó QQ nguyên hay 3x−2x−23 nguyên khi và chỉ khi x−2x−2 thuộc ước của 33
Giải ra tìm được các giá trị x=1;x=9;x=25x=1;x=9;x=25 (TMĐK).
Vậy x=1;x=9;x=25x=1;x=9;x=25.