Ta có :\(\left(x^2-1\right)\left(x+3\right)\left(x+5\right)=m\left(1\right)\)

\(\left(x+1\right)\left(x+3\right)\left(x-1\right)\left(x+5\right)=m\)

\(\left(x^2+4x+3\right)\left(x^2+4x-5\right)=m\left(2\right)\)

Đặt \(y=x^4+4x+4=\left(x+2\right)^2\ge0\) với mọi\(x\)

Khi đó (2) có dạng \(\left(y-1\right)\left(y-9\right)=m\) hay \(y^2-10y+9-m=0\left(3\right)\)

phương trình (1) có bốn nghiệm phân biệt tương đương với phương trình (3) có hai nghiệm dương phân biệt \(y_1>y_2\)>0 khi và chỉ khi \(\left\{{}\begin{matrix}\Delta'=16+m>0\\y_1+y_2=10>0\\y_1y_2=9-m>0\end{matrix}\right.hay-16< m< 9\left(4\right)\)

khi \(y_{1;}y_2\) là 2no dương phân biệt của phương trình (3) thì phương trình (2) 

\(x^2+4x+4-y_1=0\) hoặc \(x^2+4x+4-y_2=0\)

Gọi \(x_1,x_2\) là hai nghiệm phân biệt của phương trình :\(x^2+4x+4-y_1=0\left(5\right)\)

Gọi \(x_3,x_4\) là hai nghiệm phân biệt của phương trình :\(x^2+4x+4-y_2=0\left(6\right)\)

Ap dụng định lí viet cho các phương trình (6),(3),(5) ta có 

\(\dfrac{1}{x_1}+\dfrac{1}{x_2}+\dfrac{1}{x_3}+\dfrac{1}{x_4}\)

=\(\dfrac{x_1+x_2}{x_1x_2}+\dfrac{x_3+x_4}{x_3x_4}\)

=\(\dfrac{-4}{4-y_1}+\dfrac{-4}{4-y_2}\)

\(\dfrac{4\left(y_1+y_2\right)-32}{16-4\left(y_1+y_2\right)+y_1y_2}\)

=\(\dfrac{40-32}{16-40+9-m}\)

\(\dfrac{8}{-15-m}\)=\(-\)1

suy ra m=-1 (thảo mãn)

Vậy với m=-1 thì phương trình \(\left(x^2-1\right)\left(x+3\right)\left(x+5\right)=m\left(1\right)\) có 4 no phân  biệt \(x_1,x_2\) \(x_3,x_4\) thoả mãn \(\dfrac{1}{x_1}+\dfrac{1}{x_2}+\dfrac{1}{x_3}+\dfrac{1}{x_4}\)=-1

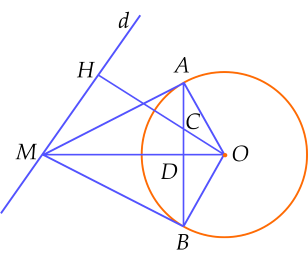
a,Do MA,MB là hai tiếp tuyến của đường tròn (O) nên MA\(\perp\)OA, MB\(\perp\)OB

suy ra  \(\widehat{MAO}=\widehat{MBO}=90^O\)

Gọi I là trung điểm của OM :IO=IM=\(\dfrac{OM}{2}\)(1)

Xét \(\Delta\) MAO vuông tại A :có AI là đường trung tuyến: AI =\(\dfrac{OM}{2}\)(2)

\(\Delta\)MBO vuông tại B có BI là đường trung tuyến :BI=\(\dfrac{OM}{2}\)(3)

Từ (1) ,(2),(3) suy ra IO=IM=AI=BI=\(\dfrac{OM}{2}\)

Vậy tứ giác MAOB nội tiếp đường tròn tâm I,đường kính OM

b,MA=MB(vì MA,MB là hai tiếp tuyến đường tròn tâm O)

mà OA =OB =R nên MO là đường trung trực của đoạn thẳng AB 

suy ra MO\(\perp\)AB tại D

H là hình chiếu của O trên đường thẳng d nên HO\(\perp\)MH

Xét \(\Delta\)ODC VÀ \(\Delta\)OHM có:

\(\widehat{MOH}\) chung

\(\widehat{ODC}=\widehat{OHM}=90^o\)

suy ra \(\Delta ODC\) đồng dạng \(\Delta OHM\)(g.g) suy ra \(\dfrac{OD}{OH}=\dfrac{OC}{OM}\) hay OC.OH=OD.OM

Xét \(\Delta\)ODA và \(\Delta\)OAM có: \(\widehat{OAM}=\widehat{ODA=90^o}\)

\(\widehat{AOD}\) chung suy ra \(\Delta\)ODA đồng dạng\(\Delta\)OAM (g.g) suy ra \(\dfrac{OD}{OA}=\dfrac{OA}{OM}\) suy ra OD.OM =\(OA^2\)=\(R^2\)

Hay OC.OH=\(R^2\)

c,Vì điểm O và đường thẳng d cố định nên H cố định do đó OH có độ dài không đổi suy ra C \(\in\) OH (4)

Từ OC.OH= \(R^2\) ta có OC =\(\dfrac{R^2}{OH}\)(5)

Từ (4), (5) suy ra điểm C cố định suy ra AB luôn đi qua điểm C cố định

Vậy khi điểm M di chuyển trên đường thẳng d thì dây AB luôn đi qua một điểm cố định

a , Thay m=-2vào phương trình (1)ta có : \(x^2+2x-3=0\)           \(\Delta=2^2-4\times1\times\left(-3\right)=16>0\)

phương trình có 2no phân biệt :\(x_1=\dfrac{-2+\sqrt{16}}{2}=1\);\(x_2=\dfrac{-2-\sqrt{16}}{2}=-3\)

Vậy với m=-2 thì phương trình (1) có nghiệm là \(x_1=1;x_2=-3\)

b,Ta có :\(\Delta=m^2-4m+4=\left(m-2\right)^2\ge0\)(luôn đúng với mọi m)

Vậy phương trình (1) luôn có 2no \(x_1;x_2\) với mọi m

Ap dụng định lí viet,ta có:\(\left\{{}\begin{matrix}x_1+x_2=m\\x_1.x_2=m-1\end{matrix}\right.\)

Theo bài A= \(\dfrac{2x_1x_2+3}{x^2_1+x^2_2+2\left(x_1x_2+1\right)}\)

=\(\dfrac{2x_1x_2+3}{\left(x_1+x_2\right)^2+2}\)

=\(\dfrac{2\left(m-1\right)+3}{m^2+2}\)

=\(\dfrac{2m+1}{m^2+2}\)

A=\(\dfrac{m^2+2-\left(m-1\right)^2}{m^2+2}\)

=1 - \(\dfrac{\left(m-1\right)^2}{m^2+2}\)                \(\left(m-1\right)^2\)>0(luôn đúng với mọi m)          \(\left(m-1\right)^2\)=0 hay m=1

A\(\le1\), dấu "=" xảy ra khi m=1

Vậy biểu thức A đạt giá trị lớn nhất khi m=1

Với \(x>0;x\ne4;x\ne9\) ta có: P= \(\left(\dfrac{4\sqrt{x}}{\sqrt{x}+2}+\dfrac{8x}{4-x}\right)\div\left(\dfrac{\sqrt{x}-1}{x-2\sqrt{x}}-\dfrac{2}{\sqrt{x}}\right)\)

P =\(\dfrac{4\sqrt{x}\left(\sqrt{x}-2\right)-8x}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\div\dfrac{\sqrt{x}-1-2\left(\sqrt{x}-2\right)}{\sqrt{x}\left(\sqrt{x}-2\right)}\)

P=\(\dfrac{-4x-8\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\div\dfrac{-\sqrt{x}+3}{\sqrt{x}\left(\sqrt{x}-2\right)}\)

P= \(\dfrac{-4\sqrt{x}\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}.\dfrac{\sqrt{x}\left(\sqrt{x}-2\right)}{-\sqrt{x}+3}\)

P=\(\dfrac{-4x}{-\sqrt{x}+3}\)

P=\(\dfrac{4x}{\sqrt{x}-3}\) vậy với \(x>0;x\ne4;x\ne9\) thì P =\(\dfrac{4x}{\sqrt{x}-3}\)

Gọi vận tốc của bạn Hoa lúc đi là \(x\)\(\left(km/h\right)\)\(\left(x>0\right)\).

Thời gian bạn Hoa đi từ nhà đến địa điểm A là \(\dfrac{24}{x}\)(giờ)

Thời gian bạn Hoa đi một nửa quãng đường về là \(\dfrac{12}{x}\)(giờ)

Vận tốc của bạn Hoa đi một nửa quãng đường còn lại lúc về nhà là \(x+4\) (\(km/h\))

Thời gian bạn Hoa đi nửa quãng đường còn lại lúc về nhà là \(\dfrac{12}{x+4}\)(giờ)

Do thời gian về ít hơn thời gian đi là 15 phút (đổi bằng \(\dfrac{1}{4}\) giờ ) nên ta có phương trình:

\(\dfrac{24}{x}-\dfrac{12}{x}-\dfrac{12}{x+4}=\dfrac{1}{4}\)

\(\dfrac{12}{x}-\dfrac{12}{x+4}=\dfrac{1}{4}\)             

\(x^2+4x-192=0\)

\(\Delta=4^2-4\times1\times\left(-192\right)=784>0\)

phương trình có 2no phân biệt :\(x_1=\dfrac{-4+\sqrt{784}}{2}=12\)(thoả mãn);\(x_2=\dfrac{-4-\sqrt{784}}{2}=-16\)(loại)

Vậy vận tốc của bạn Hoa lúc đi là 12\(km/h\)