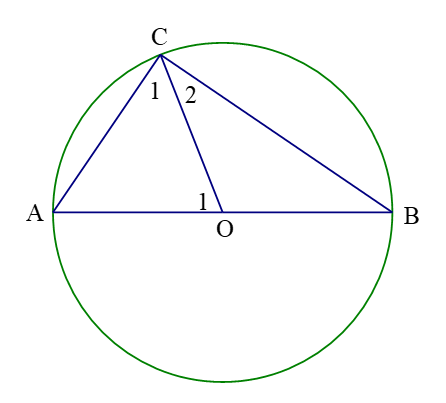
Tam giác $OAC$ có ba cạnh bằng nhau $\left(AC=OA=OC\right)$ nên là tam giác đều

Suy ra $\hat{A}=\widehat{C^1}=\widehat{O^1}=60^{\circ }$.

Ta có: $OAC$ có $OB=OC$ nên cân tại $O$ suy ra $\hat{B}=\widehat{C^2}$;

$\widehat{O^1}$ là góc ngoài của $\Delta OBC$.

Do đó $\widehat{O^1}=\hat{B}+\widehat{C^2}=2\hat{B}=2\widehat{C^2}$

$\hat{B}=\widehat{C^2}=\genfrac{}{}{0ex}{}{1}{2}\widehat{O^1}=30^{\circ }$

$\widehat{ACB}=\widehat{C^1}+\widehat{C^2}=90^{\circ }$

Vậy $\hat{A}=60^{\circ };\hat{B}=30^{\circ };\hat{C}=90^{\circ }$.

$\Delta CAB$ có trung tuyến $CO$ bằng nửa cạnh đối xứng $AB$ nên vuông tại $C$ với $\widehat{ACB}=90^{\circ }$

Suy ra $\hat{A}=60^{\circ }$ và $\hat{B}=30^{\circ }$

Vậy $\Delta ABC$ có $\hat{C}=90^{\circ };\hat{A}=60^{\circ };\hat{B}=30^{\circ }$

a) Vẽ đường tròn $(C;2$ cm$)$

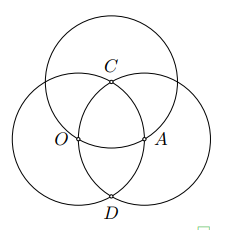
b) Đường tròn $(O;2$ cm$)$ và $(A;2$ cm$)$ cắt nhau tại $C$, $D$, điểm $A$ nằm trên đường tròn tâm $O$ nên:

$OC=OD=2$ cm, $AC=AD=2$ cm.

Suy ra $OC=CA=2$ cm.

Do đó đường tròn $(C;2$ cm$)$ đi qua hai điểm $O$ và $A$