✞ঔৣⓄⓡⓔⓚⓘঔৣ✞
Giới thiệu về bản thân



































Trong trường hợp này, việc đưa về cùng số mũ sẽ dễ hơn vì 90 và 60 đều có ước chung là 30.
Ta có: 290=(23)30=830 360=(32)30=930
Bây giờ, chúng ta so sánh 830 và 930. Vì 8<9, nên 830<930.
Vậy, 290<360.
bạn chỉ cần ra câu hỏi bạn không làm được hoặc khó hiểu thì tất cả mọi người ở diễn đán OLM sẽ giúp bạn.
ko có gì đâu.
Chiếc bút chì màu xanh.
Chiếc bút chì màu xanh.
Tham khảo:
Lời giải
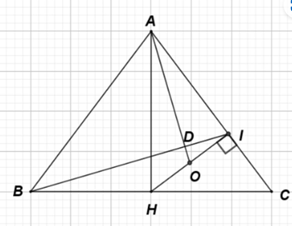
a) Vì tam giác ABC cân tại A nên AB = AC
Vì H là trung điểm của BC nên HA = HC
Xét tam giác AHB và tam giác AHC có
AH là cạnh chung
AB = AC (chứng minh trên)
HA = HC (chứng minh trên)
Do đó ΔAHB = ΔAHC (c.c.c)
Suy ra ˆAHB=ˆAHC (hai góc tương ứng)
Mà ˆAHB+ˆAHC=180∘
Suy ra ˆAHB=ˆAHC=90∘
Hay AH ⊥ BC
Vì tam giác HIC vuông tại I nên ˆIHC+ˆICH=90∘ (trong tam giác vuông, tổng hai góc nhọn bằng 90°)
Mà ˆAHO+ˆIHC=ˆAHC=90∘
Suy ra ˆAHO=ˆBCI
Vậy ˆAHO=ˆBCI.
b) Xét ΔAHI và ΔHCI có:
ˆAHI=ˆHCI (chứng minh câu a)
ˆAIH=ˆCIH(=90∘)
Do đó (g.g)
Suy ra AH . IC = HI . HC
Mà HI = 2. HO; HC = BC2
Suy ra HI . HC = 2 . HO . BC2 = HO . BC
Vậy AH . IC = HI . HC = HO . BC
c) Vì AH . IC = HO . BC nên AHHO=BCIC
Xét ΔAHO và ΔBCI có:
AHHO=BCIC (chứng minh trên)
ˆAHO=ˆBCI (chứng minh câu a)
Suy ra (c.g.c)
d) Vì nên ˆHAO=ˆCBI
Gọi giao điểm của AO và BI là D
Xét tam giác ABD có ˆABD+ˆADB+ˆDAB=180∘ (tổng ba góc trong một tam giác)
Hay ˆABD+ˆDAH+ˆBAH+ˆADB=180∘
Mà ˆHAD=ˆCBI
Suy ra ˆABD+ˆCBI+ˆBAH+ˆADB=180∘
Nên ˆABH+ˆBAH+ˆADB=180∘
Lại có ˆABH+ˆBAH=90∘ (vì tam giác AHB vuông tại H)
Suy ra ˆADB=90∘
Nên AO ⊥ BI
Vậy AO ⊥ BI.
tham khảo nha.