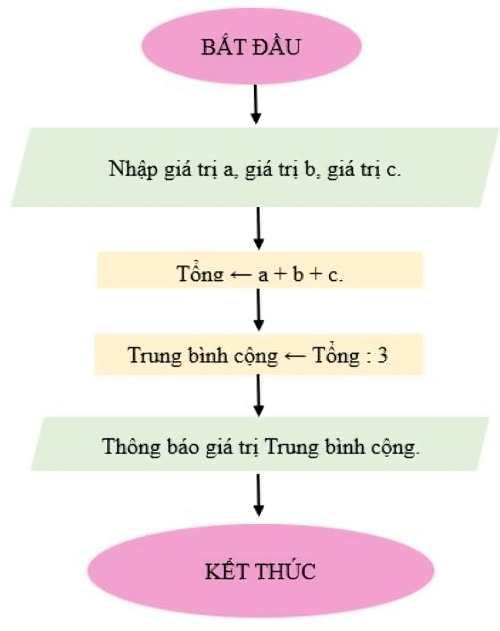
a)

- Yếu tố đã cho của bài toán: 3 số a, b, c.

- Yêu cầu cần đạt: Giá trị trung bình cộng của 3 số a, b, c.

b) Sơ đồ khối mô tả thuật toán có thể như sau:

a) Ô D2 có kiểu dữ liệu Whole Number.

Giải thích: Ô D2 có giá trị là 2002, đây là một số nguyên. Kiểu dữ liệu số nguyên tương ứng với kiểu Whole Number trong công cụ xác thực dữ liệu của phần mềm bảng tính. 2002 là năm sinh nhưng trong công cụ xác thực dữ liệu chỉ có kiểu Date - ngày sinh nên sử dụng kiểu Whole number là hợp lí nhất.

b) Sử dụng hàm SUMIF để tính tổng theo điều kiện. Công thức tính tổng số tiền của những người sinh năm 2002 đã ủng hộ được là:

=SUMIF(D2:D9,2002,E2:E9)

a) Công thức đếm số người có số ngày công lớn hơn 27 là:

=COUNTIF(C2:C9,">27")

b) Có thể sử dụng hàm IF lồng để tính tiền thưởng cho ô E2. Công thức có thể như sau:

=IF(C2>28,200000,IF(C2>26,100000,0))

Vì các điểm phân biệt nằm trên một đường tròn nên ba điểm bất kì luôn tạo thành một tam giác.

Có 21 điểm được tô bằng 4 màu, do đó có ít nhất 6 điểm có cùng màu.

Giả sử có 6 điểm cùng màu đỏ là $A,B,C,D,E,F$

Nối 5 đoạn $AB,AC,AD,AE,AF$ và tô bằng hai màu nâu, đen khi đó có ít nhất 3 đoạn cùng màu, giả sử $AB,AC,AD$ được tô cùng màu đen

Xét $\Delta BCD$, xảy ra hai khả năng:

TH1: Nếu 3 cạnh $BC,BD,DC$ được tô cùng màu nâu thì tam giác $BCD$ có ba đỉnh cùng màu đỏ, ba cạnh cùng màu nâu (thỏa mãn)

TH2: Nếu ba cạnh $BC,BD,DC$ có ít nhất một cạnh màu đen, giả sử $BC$ đen, khi đó tam giác $ABC$ có ba đỉnh cùng màu đỏ, ba cạnh cùng màu đen (thỏa mãn)

Vậy luôn có một tam giác có ba đỉnh cùng màu và ba cạnh cùng màu.

Gọi giao điểm hai đường chéo của hình chữ nhật là $O$.

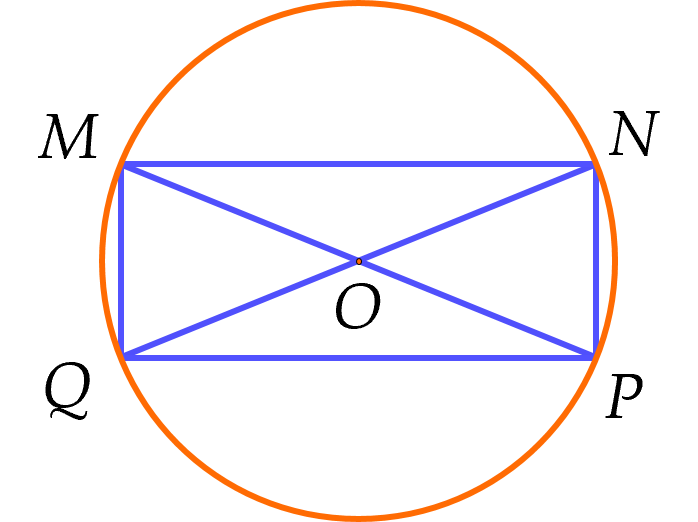
Gọi $x,y$ (m) lần lượt là hai kích thước của mảnh vườn $(x>0,y>0)$ và $R$ (m) là bán kính đường tròn ngoại tiếp mảnh vườn.

Áp dụng định lí Pythagore trong tam giác vuông $MNP$, ta có:

x2+y2=MP2x2+y2=MP2

Suy ra R2=OM2=x2+y24R2=OM2=4x2+y2​

Theo đề bài $xy=640$ m2

Diện tích $4$ phần đất mở rộng là: S=St−SMNPQ=πR2−xy=π.(x2+y24)−xy≥π.2xy4−xyS=St​−SMNPQ​=πR2−xy=π.(4x2+y2​)−xy≥π.42xy​−xy (theo bất đẳng thức Cauchy)

Do đó $S\ge 320\pi -640\approx 365,31$ m2.

Dấu "=" xảy ra khi x=y=810x=y=810​ (thoả mãn).

Vậy diện tích nhỏ nhất của $4$ phần đất được trồng thêm hoa khoảng $365,31$ m2.

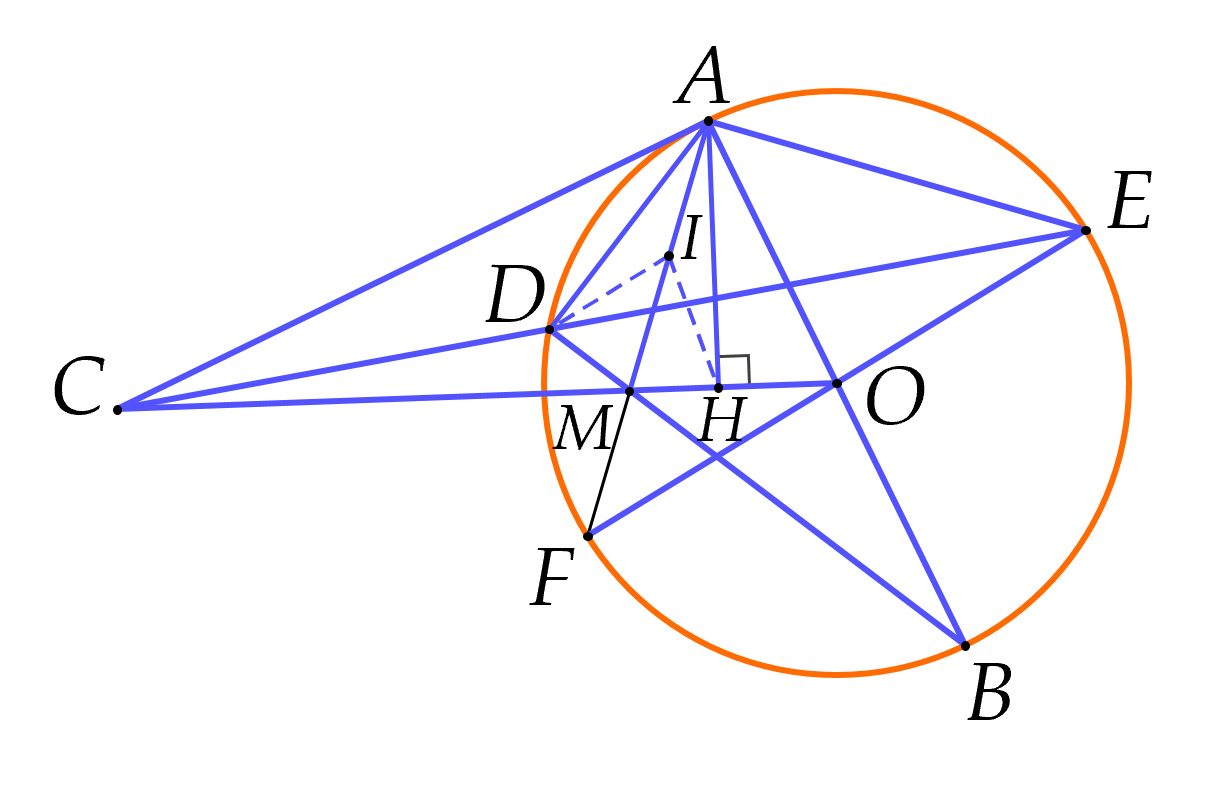
a) Gọi $I$ là trung điểm của $AM$.

Ta có ADB^=90∘ADB=90∘ (góc nội tiếp chắn nửa đường tròn) hay ADM^=90∘ADM=90∘

Suy ra $\Delta ADM$ là tam giác vuông tại $D$ có $DI$ là đường trung tuyến nên AI=DI=MI=AM2AI=DI=MI=2AM​ (1)

Do $H$ là hình chiếu vuông góc của điểm $A$ trên $CO$ nên $AH\perp CO$

Suy ra $\Delta AHM$ là tam giác vuông tại $H$ có $HI$ là đường trung tuyến nên: AI=HI=MI=AM2AI=HI=MI=2AM​ (2)

Từ (1) và (2) suy ra $AI=DI=MI=HI$,

Do đó bốn điểm $A;D;M;H$ cùng thuộc một đường tròn.

Vậy $ADMH$ là tứ giác nội tiếp.

b) Ta có CAD^+DAO^=90∘CAD+DAO=90∘

CEA^+CEB^=AEB^=90∘CEA+CEB=AEB=90∘ (góc nội tiếp chắn nửa đường tròn).

Mà DAO^=CEB^DAO=CEB (cùng chắn DB⌢DB⌢)

Do đó CAD^=CEA^CAD=CEA

Do đó $\Delta CAD\backsim \Delta CEA$ (g.g)

Suy ra CACE=CDCACECA​=CACD​ hay CA2=CD.CECA2=CD.CE (1)

 Mặt khác $\Delta ACO\backsim \Delta HCA$ (g.g)

Suy ra CA2=CH.COCA2=CH.CO (2)

Từ (1) và (2) suy ra: $CD.CE=CH.CO$

a) Gọi $I$ là trung điểm của $AM$.

Ta có ADB^=90∘ADB=90∘ (góc nội tiếp chắn nửa đường tròn) hay ADM^=90∘ADM=90∘

Suy ra $\Delta ADM$ là tam giác vuông tại $D$ có $DI$ là đường trung tuyến nên AI=DI=MI=AM2AI=DI=MI=2AM​ (1)

Do $H$ là hình chiếu vuông góc của điểm $A$ trên $CO$ nên $AH\perp CO$

Suy ra $\Delta AHM$ là tam giác vuông tại $H$ có $HI$ là đường trung tuyến nên: AI=HI=MI=AM2AI=HI=MI=2AM​ (2)

Từ (1) và (2) suy ra $AI=DI=MI=HI$,

Do đó bốn điểm $A;D;M;H$ cùng thuộc một đường tròn.

Vậy $ADMH$ là tứ giác nội tiếp.

b) Ta có CAD^+DAO^=90∘CAD+DAO=90∘

CEA^+CEB^=AEB^=90∘CEA+CEB=AEB=90∘ (góc nội tiếp chắn nửa đường tròn).

Mà DAO^=CEB^DAO=CEB (cùng chắn DB⌢DB⌢)

Do đó CAD^=CEA^CAD=CEA

Do đó $\Delta CAD\backsim \Delta CEA$ (g.g)

Suy ra CACE=CDCACECA​=CACD​ hay CA2=CD.CECA2=CD.CE (1)

 Mặt khác $\Delta ACO\backsim \Delta HCA$ (g.g)

Suy ra CA2=CH.COCA2=CH.CO (2)

Từ (1) và (2) suy ra: $CD.CE=CH.CO$

a) Tính giá trị của biểu thức $A$ khi $x=4.$

Thay $x=4$ (thỏa mãn điều kiện) vào biểu thức $A$ ta được:

A=24−1=2.A=4​−12​=2.

b) Với $x\ge 0,x\ne 1$ ta có P=B−A=xx+1+4x−1−2x−1P=B−A=x​+1x​​+x−14​−x​−12​

=x(x−1)+4−2(x+1)(x−1)(x+1)=(x​−1)(x​+1)x​(x​−1)+4−2(x​+1)​

=x−3x+2(x−1)(x+1)=(x​−1)(x​+1)x−3x​+2​

=(x−1)(x−2)(x−1)(x+1)=(x​−1)(x​+1)(x​−1)(x​−2)​

=x−2x+1.=x​+1x​−2​.

c) Với $x\ge 0,x\ne 1$ ta có P=x−2x+1=1−3x+1.P=x​+1x​−2​=1−x​+13​.

x+1≥1x​+1≥1 với mọi $x$ thỏa mãn điều kiện nên 3x+1≤3x​+13​≤3 suy ra $P\ge -2.$

Dấu bằng xảy ra khi và chỉ khi $x=0$ (thỏa mãn điều kiện).

Vậy giá trị nhỏ nhất của biểu thức $P=-2$ khi $x=0.$

a) Tính giá trị của biểu thức $A$ khi $x=4.$

Thay $x=4$ (thỏa mãn điều kiện) vào biểu thức $A$ ta được:

A=24−1=2.A=4​−12​=2.

b) Với $x\ge 0,x\ne 1$ ta có P=B−A=xx+1+4x−1−2x−1P=B−A=x​+1x​​+x−14​−x​−12​

=x(x−1)+4−2(x+1)(x−1)(x+1)=(x​−1)(x​+1)x​(x​−1)+4−2(x​+1)​

=x−3x+2(x−1)(x+1)=(x​−1)(x​+1)x−3x​+2​

=(x−1)(x−2)(x−1)(x+1)=(x​−1)(x​+1)(x​−1)(x​−2)​

=x−2x+1.=x​+1x​−2​.

c) Với $x\ge 0,x\ne 1$ ta có P=x−2x+1=1−3x+1.P=x​+1x​−2​=1−x​+13​.

x+1≥1x​+1≥1 với mọi $x$ thỏa mãn điều kiện nên 3x+1≤3x​+13​≤3 suy ra $P\ge -2.$

Dấu bằng xảy ra khi và chỉ khi $x=0$ (thỏa mãn điều kiện).

Vậy giá trị nhỏ nhất của biểu thức $P=-2$ khi $x=0.$

1) Bảng tần số và bảng tần số tương đối cho dữ liệu cỡ giày của các bạn nam khối 9 trong trường.

2) Gọi số cần tìm là a1a2a3a4‾a1​a2​a3​a4​​ trong đó ai∈N,ai​∈N, 0≤ai ≤9,a1≠00≤ai​ ≤9,a1​=0 là các chữ số.

Chọn a1a1​ có $9$ cách.

Chọn a2a2​ có $9$ cách.

Chọn a3a3​ có $8$ cách.

Chọn a4a4​ có $7$ cách.

Số cách chọn là $\mathrm{9.9.8.7}=4536$ cách.

Vậy số phần tử của không gian mẫu là $4536$.