0

1) Diện đáy của hình chóp tứ giác đều là

$6250.3:30=625$ (cm22)

Độ dài cạnh đáy của hình chóp tứ giác đều là

625=25625​=25 (cm)

2) 

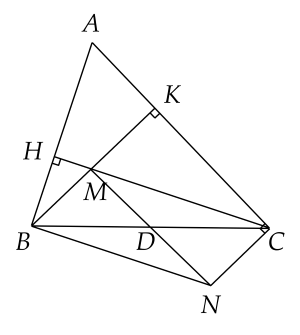
a) Xét tứ giác $BMCN$ có hai đường chéo $MN$ và $BC$ cắt nhau tại trung điểm mỗi đường, đo đó $BMNC$ là hình bình hành.

b) Vì $BMCN$ là hình bình hành nên ta suy ra $BM//NC$. Vậy $BKCN$ là hình thang. Mặt khác do BKC^=90∘BKC=90∘ nên $BMCN$ là hình thang cân.

c) Để $BMCN$ là hình thoi thì $MD\perp BC$.

Mặt khác ta cũng có $AM\perp BC$ (giao điểm ba đường cao).

Kẻ đường thẳng $d$ vuông góc với $BC$, từ đây ta suy ra

$MD//d$ và $AM//d$. Vậy theo tiên đề Euclid, ta có 3 điểm $M,A,D$ thẳng hàng, hay $AD$ vừa là đường cao và vừa là đường trung tuyến của tam giác $ABC$.

Dễ dàng chứng minh được $\Delta AMD=\Delta ADC$, từ đó suy ra $AB=AC$, hay tam giác $ABC$ cân tại $A$.

Vậy để $BMCN$ là hình thoi thì $\Delta ABC$ là tam giác cân.

Gọi phương trình đường thẳng $AB$ là $y=ax+b$ $(a,b\in \mathbb{R}$ và $a\ne 0)$.

Ta có $A(-3;0)\in AB$ suy ra $0=a.(-3)+b$ hay $b=3a$.

$B(0;2)\in AB$ suy ra $2=a.0+b$ hay $b=2$. Từ đó suy ra a=23a=32​.

Vậy phương trình đường thẳng $AB$ là y=23x+2y=32​x+2.

a) Điều kiện: $x\ne 0,x\ne -5$.

b) A=x2+2x2x+10+x−5x−5x−502x(x+5)A=2x+10x2+2x​+xx−5​−2x(x+5)5x−50​

=x2+2x2x+10+x−5x+50−5x2x(x+5)=2x+10x2+2x​+xx−5​+2x(x+5)50−5x​

=x3+2x2+2x2−50+50−5x2x(x+5)=2x(x+5)x3+2x2+2x2−50+50−5x​

=x(x2+2x+2x−5)2x(x+5)=2x(x+5)x(x2+2x+2x−5)​

=x2−x+5x−52(x+5)=2(x+5)x2−x+5x−5​

=(x−1)(x+5)2(x+5)=x−12=2(x+5)(x−1)(x+5)​=2x−1​

Nếu giá trị của biểu thức bằng $1$ thì giá trị của x−122x−1​ cũng bằng $1$. Ta có : x−12=12x−1​=1 khi $x-1=2$ hay $x=3$. 

Vì $x=3$ thoả mãn điều kiện nên đó là giá trị phải tìm.

c) Tương tự x−12=−122x−1​=−21​ khi $x-1=-1$ hay $x=0$ (không thoả mãn điều kiện). Vậy không có giá trị nào của $x$ để phân thức có giá trị bằng −12−21​.

d) Tương tự x−12=−32x−1​=−3 khi $x-1=-6$ hay $x=-5$ (không thoả mãn điểu kiện). Vậy không có giá trị nào của $x$ để phân thức có giá trị bằng $-3.$

a)

 $2x(x-3y)-25(3y-x)$

$=2x(x-3y)+25(x-3y)$

$=(2x+25)(x-3y)$

b) 36x2−24x+436x2−24x+4;

=(6x)2−2.6x.2+22=(6x)2−2.6x.2+22

=(6x−2)2=(6x−2)2

c) (3x+2)2+2.(3x+2).(3x−1)+(3x−1)2(3x+2)2+2.(3x+2).(3x−1)+(3x−1)2.

=(3x+2+3x−1)2=(3x+2+3x−1)2

=(6x+1)2=(6x+1)2