1.

Vì A nằm giữa O,B nên

Ta có: OA+AB=OB

           2cm+AB=OB

Vì điểm A là trung điểm của đoạn thẳng OB, nên

⇒OA=AB\(\left(\right.\)2cm=2cm\(\left.\right)\)

            OB=OA+OB

             OB=2+2

             OB=4 cm

2.

a\(\left.\right)\) Điểm I và C là nằm trong góc BAD

b\(\left.\right)\) Một số góc bẹt trong hình là: góc BID; góc AIC

c\(\left.\right)\) Các góc AIC, ACD,BCD và BAD xếp theo thứ tự tăng dần là:

BAD; ACD; BCD và AIC

Số học sinh tốt là:

45*4/15=12 học sinh

Số học sinh khá là:

12*5/3=20 học sinh

Số học sinh xếp loại khá là:

45-12-20=13 học sinh

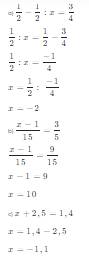
+ =131+132+133+…+160S=311​+321​+331​+…+601​

<(130+130+…+130)+(140+140+…+140)+(150+150+…+150)S<(301​+301​+…+301​)+(401​+401​+…+401​)+(501​+501​+…+501​)

<1030+1040+1050<4860=45;S<3010​+4010​+5010​<6048​=54​;

+ >(140+140+…+140)+(150+150+…+150)+(160+160+…+160)S>(401​+401​+…+401​)+(501​+501​+…+501​)+(601​+601​+…+601​)

>1040+1050+1060>35.S>4010​+5010​+6010​>53​.

a: Số quả bóng bán được trong tháng 1 là \(3 \cdot 5 = 15 \left(\right. q u ả \left.\right)\)

Số quả bóng bán được trong tháng 2 là \(4 \cdot 5 = 20 \left(\right. q u ả \left.\right)\)

Số quả bóng bán được trong tháng 3 là \(2 \cdot 5 = 10 \left(\right. q u ả \left.\right)\)

b: Tổng số quả bóng rổ bán được trong 3 tháng là:

15+20+10=45(quả)

c: Tháng 2 bán được nhiều hơn tháng 3:

20-10=10(quả)

d: Tỉ số giữa số lượng bóng rổ bán được trong tháng 1 và tháng 2 là:

\(15 : 20 = \frac{3}{4}\)

1. a) O thuộc các đoạn thẳng: AB; CD; OA; OB; OC; OD.

b) Ta có O nằm giữa hai điểm A và B và =OA = OB =3 cm nên O là trung điểm của đoạn thẳng AB.

2. a) Số đo góc xOy bằng 30∘

b)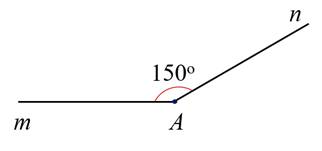 

a) \(\frac{5}{17} - \frac{25}{31} + \frac{12}{17} + \frac{- 6}{31}\)

\(= \left(\right. \frac{5}{17} + \frac{12}{17} \left.\right) + \left(\right. \frac{- 25}{31} + \frac{- 6}{31} \left.\right)\)

\(= \frac{17}{17} + \frac{- 31}{31}\)

\(= 1 + \left(\right. - 1 \left.\right) = 0\)

b) \(\frac{17}{8} : \left(\right. \frac{27}{8} + \frac{11}{4} \left.\right)\)

\(= \frac{17}{8} : \left(\right. \frac{27}{8} + \frac{22}{8} \left.\right)\)

\(= \frac{17}{8} : \frac{49}{8} = \frac{17}{8} \cdot \frac{8}{49} = \frac{17}{49}\)

c) \(\frac{1}{5} \cdot \frac{11}{16} + \frac{1}{5} \cdot \frac{5}{16} + \frac{4}{5}\)

\(= \frac{1}{5} \cdot \left(\right. \frac{11}{16} + \frac{5}{16} + 4 \left.\right)\)

\(= \frac{1}{5} \cdot \left(\right. \frac{16}{16} + 4 \left.\right)\)

\(= \frac{1}{5} \cdot \left(\right. 1 + 4 \left.\right) = \frac{1}{5} \cdot 5 = 1\)

d) \(\frac{5}{6} : 25 - 2 + \frac{- 7}{3} \cdot \frac{2}{7}\)

\(= \frac{5}{6} \cdot \frac{1}{25} - 2 + \frac{- 2}{3}\)

\(= \frac{1}{30} - \frac{6}{3} + \frac{- 2}{3}\)

\(= \frac{1}{30} - \frac{8}{3} = \frac{1}{30} - \frac{80}{30} = \frac{- 79}{30}\)

+ =131+132+133+…+160S=311​+321​+331​+…+601​

<(130+130+…+130)+(140+140+…+140)+(150+150+…+150)S<(301​+301​+…+301​)+(401​+401​+…+401​)+(501​+501​+…+501​)

<1030+1040+1050<4860=45;S<3010​+4010​+5010​<6048​=54​;

+ >(140+140+…+140)+(150+150+…+150)+(160+160+…+160)S>(401​+401​+…+401​)+(501​+501​+…+501​)+(601​+601​+…+601​)

>1040+1050+1060>35.S>4010​+5010​+6010​>53​.