Ta có a/c=c/b

⇔c2=ab

Ta lại có: (a2+c2)/(b2+c2)=(a2+ab)/(b2+ab)

                                        =a(a+b)/b(a+b)

                                        =a/b (đpcm)

a) Vẽ hình

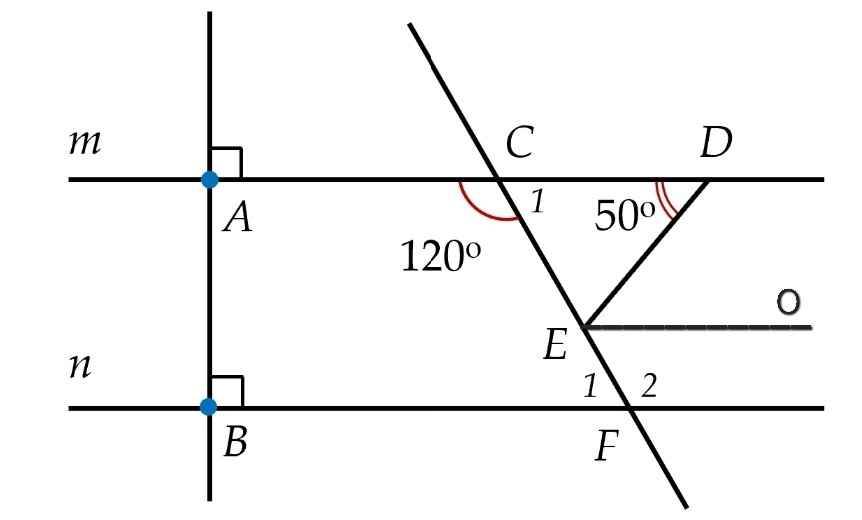 b) Ta có:

∠C₁ + ∠ACF = 180⁰ (kề bù)

⇒ ∠C₁ = 180⁰ - ∠ACF

= 180⁰ - 120⁰

= 60⁰

Do m // n (gt)

⇒ ∠F₁ = ∠C₁ = 60⁰ (so le trong)

c) Do AB ⊥ m (gt)

m // n (gt)

⇒ AB ⊥ n

d) Vẽ tia Eo // m // n như hình

Do Eo // m

⇒ ∠DEo = ∠ADE = 50⁰ (so le trong)

Do Eo // n

⇒ ∠FEo = ∠F = 60⁰ (so le trong)

⇒ ∠DEF = ∠DEo + ∠FEo

= 50⁰ + 60⁰

= 110⁰

Gọi a (quyển), b (quyển), c (quyển) lần lượt là số quyển sách ba lớp 7A, 7B, 7C đã quyên góp (a, b, c ∈ ℕ*)

Do tổng số quyển sách đã quyên góp là 180 quyển nên:

a + b + c = 180

Do số quyển sách của ba lớp 7A, 7B, 7C tỉ lệ với các số 5; 6; 4 nên:

a/5 = b/6 = c/4

Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:

a/5 = b/6 = c/4 = (a + b + c)/(5 + 6 + 4) = 180/15 = 12

a/5 = 12 ⇒ a = 12.5 = 60

b/6 = 12 ⇒ b = 12.6 = 72

c/4 = 12 ⇒ c = 12.4 = 48

Vậy số quyển sách đã quyên góp của lớp 7A, 7B, 7C lần lượt là: 60 quyển, 72 quyển, 48 quyển

a) 7/2 - (3/4 + 1/5)

= 7/2 - 19/20

= 51/20

b) 12/23 . 7/13 + 11/23 . 7/13

= 7/13 . (12/23 + 11/23)

= 7/13 . 1

= 7/13

c) |-2| - (5/9 - 2/3)² : 4/27

= 2 - 1/81 : 4/27

= 2 - 1/12

= 23/12

3/4 - (x - 2/3) = 1 1/3

3/4 - x + 2/3 = 4/3

-x = 4/3 - 3/4 - 2/3

-x = -1/12

x = 1/12

a) có EF // BC (gt)

         MN // BC ( gt)

=> EF // MN 

b) có góc CAx = góc ACB (gt)

mà 2 góc này ở vị trí so le trong

=> Ax// MN ( dấu hiệu nhận biết 2 đường thẳng //)

a, Ta có:  xy//x'y' nên xAB ^ = ABy' (hai góc so le trong).

AA' là tia phân giác của xAB nên A1 = A2 = 1/2 xAB 

BB' là tia phân giác của ABy'  nên B1 = B2 = 1/2 ABy'

Từ trên ta có A2 = B1

Mà hai góc ở vị trí so le trong, nên

=> AA' // BB/ (có 2 góc so le trong bằng nhau)

b, xy//x'y' nên A1 = AA'B (2 góc so le trong)

AA'//BB' nên A1 = AB'B(2 góc đồng vị)

Vậy AA'B = AB'B 

Trong $\widehat{AOB}$ dựng tia $Ot$ // $Ox$. (1)

Suy ra ${\hat{O}}^2+{\hat{A}}^2=180^{\circ }$ (2 góc trong cùng phía).

Khi đó ${\hat{O}}^1=\widehat{AOB}-{\hat{O}}^2=\widehat{AOB}-\left(180^{\circ }-{\hat{A}}^2\right)=\widehat{AOB}+{\hat{A}}^2-180^{\circ }={\hat{B}}^1$