

Trịnh Quang Minh
Giới thiệu về bản thân



































Bài 2:
1) Thay m = 1(TMĐK) vào hàm số y = (m - 2)x + m + 3 có
⇒ y = (1 - 2)x + 1 + 3
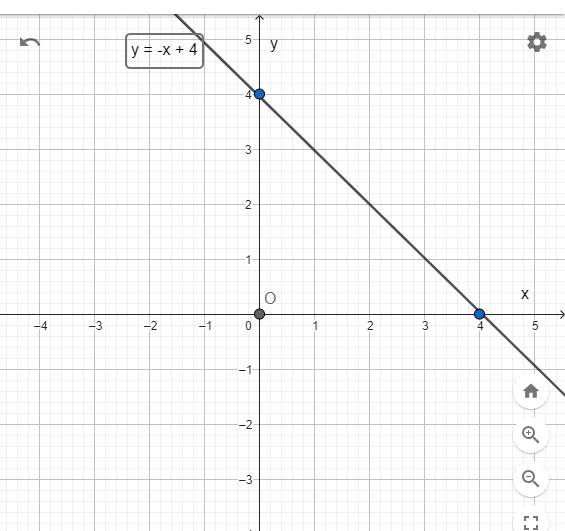
⇒ y = -x + 4
Xét (d) : y = -x + 4 có bảng
| x | 0 | 4 |
| y | 4 | 0 |
| Điểm | (0; 4) | (4; 0) |
2) Để hai đường thẳng và cắt nhau tại một điểm trên trục tung thì
⇒\(\left\{{}\begin{matrix}m-2\ne5\\m+3=-1\end{matrix}\right.\)
⇒\(\left\{{}\begin{matrix}m\ne7\\m=-2\end{matrix}\right.\)(TM) ⇒ m = -2
Vậy m = -2 thì hai đường thẳng (d)
và cắt nhau tại một điểm trên trục tung.
Bài 2:
1) Thay m = 1(TMĐK) vào hàm số y = (m - 2)x + m + 3 có
⇒ y = (1 - 2)x + 1 + 3
⇒ y = -x + 4
Xét (d) : y = -x + 4 có bảng
| x | 0 | 4 |
| y | 4 | 0 |
| Điểm | (0; 4) | (4; 0) |

2) Để hai đường thẳng và cắt nhau tại một điểm trên trục tung thì
⇒\(\left\{{}\begin{matrix}m-2\ne5\\m+3=-1\end{matrix}\right.\)
⇒\(\left\{{}\begin{matrix}m\ne7\\m=-2\end{matrix}\right.\)(TM) ⇒ m = -2
Vậy m = -2 thì hai đường thẳng (d)
và cắt nhau tại một điểm trên trục tung.
Bài 1:
1) A = \(10\sqrt{\dfrac{1}{5}}\) - \(3\sqrt{\left(2-\sqrt{5}\right)^2}\) + \(\sqrt{5}\)
= \(2\sqrt{5}\) - \(3\left(\sqrt{5}-2\right)\) +\(\sqrt{5}\)
= \(3\sqrt{5}\) - \(3\sqrt{5}\) + 6 + \(\sqrt{5}\)
= 6
B = \(\left(\dfrac{4\sqrt{x}}{\sqrt{x}+2}-\dfrac{8x}{x-4}\right):\) \(\left(\dfrac{\sqrt{x}-1}{x-2\sqrt{x}}-\dfrac{2}{\sqrt{x}}\right)\) (ĐKXĐ: x > 0; x ≠ 4)
= \(\dfrac{4x-8\sqrt{x}-8x}{x-4}:\dfrac{\sqrt{x}-1-2\sqrt{x}+4}{x-2\sqrt{x}}\)
= \(\dfrac{-4x-8\sqrt{x}}{x-4}\cdot\dfrac{x-2\sqrt{x}}{3-\sqrt{x}}\)
= \(\dfrac{-4\sqrt{x}\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\cdot\dfrac{\sqrt{x}\left(\sqrt{x}-2\right)}{3-\sqrt{x}}\)
= \(-\dfrac{4x}{3-\sqrt{x}}\)
= \(\dfrac{4x}{\sqrt{x}-3}\)
Bài 2: \(\sqrt{4x^2-4x+1}=\sqrt[3]{27}\)
⇔ \(\sqrt{\left(2x-1\right)^2}=3\)
⇔ \(\left|2x-1\right|=3\)
⇔ \(\left\{{}\begin{matrix}2x-1=3\\2x-1=-3\end{matrix}\right.\)
⇔ \(\left\{{}\begin{matrix}2x=4\\2x=-2\end{matrix}\right.\)
⇔ \(\left\{{}\begin{matrix}x=2\\x=-1\end{matrix}\right.\)
Vậy S = {2; -1}