

Bùi Tuấn Minh
Giới thiệu về bản thân



































Biểu thức �A lớn nhất khi và chỉ khi �2022+2023x2022+2023 nhỏ nhất.
Ta có: �2022≥0x2022≥0 với mọi �x. Dấu bằng xảy ra khi và chỉ khi �=0x=0.
Vậy khi �=0x=0, �A đạt giá trị lớn nhất bằng 20232023.
| GT |
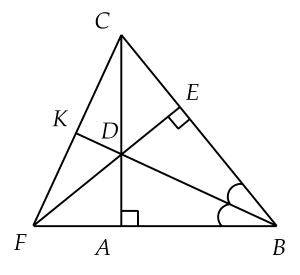
Δ���:�=90∘ΔABC:A=90∘ ��BD là phân giác của góc �B ��⊥��(�∈��)DE⊥BC(E∈AC) ��∩��={�}BA∩ED={F} ��∩��={�}BD∩FC={K} |
| KL |
a) Δ���=Δ���ΔBAD=ΔBED. b) Δ���ΔBCF cân tại �B. c) ��BD là đường trung tuyesn của Δ���ΔBCF. |
a) Xét Δ���ΔBAD và Δ���ΔBED lần lượt vuông tại �A và �E.
��BD chung.
���^=���^ABD=EBD (��BD là tia phân giác).
Suy ra Δ���=Δ���ΔBAD=ΔBED (cạnh huyền - góc nhọn).
b) Vì Δ���=Δ���(�/�ΔBAD=ΔBED(c/m phần a) nên ��=��;��=��AD=ED;BA=BE (2)
Xét Δ���ΔAFD vuông tại �A và Δ���ΔECD vuông tại �E có:
��=��(���)AD=ED(cmt)
���^=���^ADF=EDC (đối đỉnh)
Suy ra Δ���=Δ���ΔAFD=ΔECD (cạnh góc vuông - góc nhọn)
Nên ��=��AF=EC (2).
Từ (1) và (2) suy ra ��+��=��+��AF+BA=BE+EC
Hay ��=��BF=BC
Vậy Δ���ΔBCF cân tại �B.
c) Giả sử ��BD kéo dài cắt ��FC tại �K
Xét Δ���ΔBKF và Δ���ΔBKC có:
��BK là cạnh chung
���^=���^KBF=KBC (Vì ��BD là phân giác của ���^ABC )
��=��BF=BC ( chứng minh phần �)b)
Suy ra Δ���=Δ���(ΔBKF=ΔBKC( c.g.c ))
Suy ra ��=��KF=KC (hai cạnh tương ứng)
Vậy ��BK hay ��BD là đường trung tuyến của Δ���ΔBCF.
a) Tập hợp �M gồm các kết quả có thể xảy ra khi bút màu được rút ra là:
�=M= {{ xanh, đỏ, vàng, da cam, tím, trắng, hồng }}.
b) Số phần tử của tập hợp �M là 77.
Xác suất biến cố "Màu được rút ra là vàng" là: 1/717
a) Sắp xếp �(�)P(x) và �(�)Q(x) theo lũy thừa giảm dần.
�(�)=2�3+5�2−2�+2P(x)=2x3+5x2−2x+2.
�(�)=−�3−5�2+2�+6Q(x)=−x3−5x2+2x+6.
b) �(�)+�(�)=�3+8P(x)+Q(x)=x3+8.
�(�)−�(�)=3�3+10�2−4�−4P(x)−Q(x)=3x3+10x2−4x−4.
) Do tam giác ���ABC cân tại �A nên ��=��AB=AC và ���^=���^ABC=ACB.
Do ��BF là tia phân giác của ���^ABC nên ���^=���^=12���^ABF=FBC=21ABC.
Do ��CE là tia phân giác của ���^ACB nên ���^=���^=12���^ACE=ECB=21ACB.
Do đó ���^=���^ABF=ACE.
b) Xét △���△ABF và △���△ACE có:
���^=���^ABF=ACE (chứng minh trên).
��=��AB=AC (chứng minh trên).
�^A chung.
Do đó △���=△���△ABF=△ACE (g.c.g).
Suy ra ��=��AF=AE (hai cạnh tương ứng).
Tam giác ���AEF có ��=��AF=AE nên tam giác ���AEF cân tại �A.
c) Ta có ���^=���^FBC=ECB nên ���^=���^IBC=ICB.
Tam giác ���IBC có ���^=���^IBC=ICB nên tam giác ���IBC cân tại �I.
Do đó ��=��IB=IC.
���^=���^EIB=FIC (đối đỉnh).
��=��IB=IC (chứng minh trên).
���^=���^EBI=FCI (chứng minh trên).
Do đó Δ���=Δ���ΔEIB=ΔFIC (g.c.g).
Suy ra ��=��IE=IF (hai cạnh tương ứng).
Tam giác ���IEF có ��=��IE=IF nên tam giác ���IEF cân tại �I.
a) Tập hợp các kết quả có thể xảy ra đối với học sinh được chọn ra là:
G={Mỹ; Anh; Pháp; Thái Lan; Việt Nam; Canada; Thụy Sĩ; Nga; Brasil}}.
b) Trong 99 nước trên có các nước thuộc châu Á là: Việt Nam và Thái Lan.
Do đó có 22 kết quả thuận lợi cho biến cố "Học sinh được chọn ra đến từ châu Á" là: Việt Nam; Thái Lan.
Khi đó xác suất của biến cố "Học sinh được chọn ra đến từ châu Á" bằng:2/9
a) Ngày 5/2/2023 trong tuần đầu tiên của tháng 02/2023, hộ gia đình tiêu thụ lượng điện it nhất.
b)Trong tuần đầu tiên của tháng 02/2023, hộ gia đình đó tiêu thụ hết 112 kW.h điện.
Trung bình mỗi ngày tiêu thụ 16 kW.h điện.
c)Trong 7 ngày đầu tiên của tháng 02/2023, ngày tiêu thụ điện nhiều nhất tăng 66,67 %% so với ngày tiêu thụ điện it nhất