

Nguyễn Quốc Huy
Giới thiệu về bản thân



































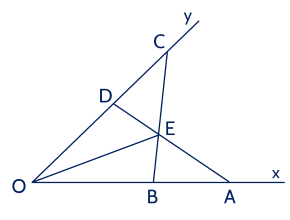
a) Xét và , có
(giả thiết);
chung;
(giả thiết).
Do đó (c.g.c)
(hai cạnh tương ứng).
b) Do và nên .
Mà (chứng minh trên)
; (hai góc tương ứng)
Mặt khác
Xét và có
(chứng minh trên);
(chứng minh trên);
(chứng minh trên)
Do đó (g.c.g).
c) Vi (chứng minh trên) nên (hai cạnh tương ứng).
Xét và có (chứng minh trên);
cạnh chung;
(giả thiết).
Do đó (c.c.c)
(hai góc tương ứng)
là tia phân giác của .
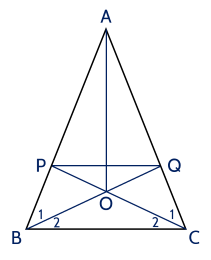
a) cân tại nên .
Vì và là đường phân giác của nên , .
Do đó .
Suy ra cân tại .
b) Vì là giao điểm các đường phân giác và trong nên là giao điểm ba đường phân giác trong .
Do đó, cách đều ba cạnh và .
c) Ta có cân tại là đường phân giác của góc nên đồng thời là trung tuyến và đường cao của .
Vậy đường thẳng đi qua trung điểm của đoạn thẳng và vuông góc với nó.
d) Ta có (g.c.g)
(hai cạnh tương ứng).
e) Ta có , (1);
(2).
Lại có (tam giác cân tại ) (3).
Từ (1), (2) và (3) suy ra .
Vậy tam giác cân tại .

a) Xét và , có
(giả thiết);
chung;
(giả thiết).
Do đó (c.g.c)
(hai cạnh tương ứng).
b) Do và nên .
Mà (chứng minh trên)
; (hai góc tương ứng)
Mặt khác
Xét và có
(chứng minh trên);
(chứng minh trên);
(chứng minh trên)
Do đó (g.c.g).
c) Vi (chứng minh trên) nên (hai cạnh tương ứng).
Xét và có (chứng minh trên);
cạnh chung;
(giả thiết).
Do đó (c.c.c)
(hai góc tương ứng)
là tia phân giác của .

a) Xét và , có
(giả thiết);
chung;
(giả thiết).
Do đó (c.g.c)
(hai cạnh tương ứng).
b) Do và nên .
Mà (chứng minh trên)
; (hai góc tương ứng)
Mặt khác
Xét và có
(chứng minh trên);
(chứng minh trên);
(chứng minh trên)
Do đó (g.c.g).
c) Vi (chứng minh trên) nên (hai cạnh tương ứng).
Xét và có (chứng minh trên);
cạnh chung;
(giả thiết).
Do đó (c.c.c)
(hai góc tương ứng)
là tia phân giác của .

a) Xét và , có
(giả thiết);
chung;
(giả thiết).
Do đó (c.g.c)
(hai cạnh tương ứng).
b) Do và nên .
Mà (chứng minh trên)
; (hai góc tương ứng)
Mặt khác
Xét và có
(chứng minh trên);
(chứng minh trên);
(chứng minh trên)
Do đó (g.c.g).
c) Vi (chứng minh trên) nên (hai cạnh tương ứng).
Xét và có (chứng minh trên);
cạnh chung;
(giả thiết).
Do đó (c.c.c)
(hai góc tương ứng)
là tia phân giác của .

a) cân tại nên .
Vì và là đường phân giác của nên , .
Do đó .
Suy ra cân tại .
b) Vì là giao điểm các đường phân giác và trong nên là giao điểm ba đường phân giác trong .
Do đó, cách đều ba cạnh và .
c) Ta có cân tại là đường phân giác của góc nên đồng thời là trung tuyến và đường cao của .
Vậy đường thẳng đi qua trung điểm của đoạn thẳng và vuông góc với nó.
d) Ta có (g.c.g)
(hai cạnh tương ứng).
e) Ta có , (1);
(2).
Lại có (tam giác cân tại ) (3).
Từ (1), (2) và (3) suy ra .
Vậy tam giác cân tại .

a) Xét và , có
(giả thiết);
chung;
(giả thiết).
Do đó (c.g.c)
(hai cạnh tương ứng).
b) Do và nên .
Mà (chứng minh trên)
; (hai góc tương ứng)
Mặt khác
Xét và có
(chứng minh trên);
(chứng minh trên);
(chứng minh trên)
Do đó (g.c.g).
c) Vi (chứng minh trên) nên (hai cạnh tương ứng).
Xét và có (chứng minh trên);
cạnh chung;
(giả thiết).
Do đó (c.c.c)
(hai góc tương ứng)
là tia phân giác của .

a) cân tại nên .
Vì và là đường phân giác của nên , .
Do đó .
Suy ra cân tại .
b) Vì là giao điểm các đường phân giác và trong nên là giao điểm ba đường phân giác trong .
Do đó, cách đều ba cạnh và .
c) Ta có cân tại là đường phân giác của góc nên đồng thời là trung tuyến và đường cao của .
Vậy đường thẳng đi qua trung điểm của đoạn thẳng và vuông góc với nó.
d) Ta có (g.c.g)
(hai cạnh tương ứng).
e) Ta có , (1);
(2).
Lại có (tam giác cân tại ) (3).
Từ (1), (2) và (3) suy ra .
Vậy tam giác cân tại .

a) Xét và , có
(giả thiết);
chung;
(giả thiết).
Do đó (c.g.c)
(hai cạnh tương ứng).
b) Do và nên .
Mà (chứng minh trên)
; (hai góc tương ứng)
Mặt khác
Xét và có
(chứng minh trên);
(chứng minh trên);
(chứng minh trên)
Do đó (g.c.g).
c) Vi (chứng minh trên) nên (hai cạnh tương ứng).
Xét và có (chứng minh trên);
cạnh chung;
(giả thiết).
Do đó (c.c.c)
(hai góc tương ứng)
là tia phân giác của .
a) Xét và có
(giả thiết);
cạnh chung;
( là tia phân giác).
Vậy (cạnh huyền - góc nhọn).
b) (chứng minh trên)
(hai cạnh tương ứng).
Gọi là giao điểm của và .
Xét và , có
(chứng minh trên);
( là tia phân giác);
chung.
Do đó (c.g.c)
(hai góc tương ứng)
Mà nên .
Vậy .