Gọi $D$ là giao điểm của $AG$ và $BC\Rightarrow DB=DC$.

Ta có BG=23BEBG=32​BE; CG=23CFCG=32​CF (tính chất trọng tâm).

Vì $BE=CF$ nên $BG=CG\Rightarrow △BCG$ cân tại $G$

⇒GCB^=GBC^⇒GCB=GBC

Xét $△BFC$ và $△CEB$ có $CF=BE$ (giả thiết);

GCB^=GBC^GCB=GBC (chứng minh trên);

$BC$ là cạnh chung.

Do đó $△BFC=△CEB$ (c.g.c)

⇒FBC^=ECB^⇒FBC=ECB (hai góc tưong ứng)

$\Rightarrow △ABC$ cân tại $A\Rightarrow AB=AC$.

Từ đó suy ra $△ABD=△ACD$ (c.c.c)

⇒ADB^=ADC^⇒ADB=ADC. (hai góc tương ứng)

Mà ADB^+ADC^=180∘⇒ADB^=ADC^=90∘⇒AD⊥BCADB+ADC=180∘⇒ADB=ADC=90∘⇒AD⊥BC hay $AG\perp BC$.

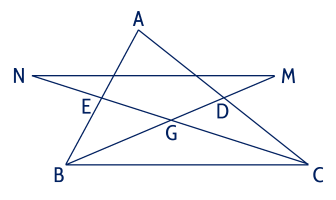
a) Ta có $DM=DG\Rightarrow GM=2GD$.

Ta lại có $G$ là giao điểm của $BD$ và $CE\Rightarrow G$ là trọng tâm của tam giác $ABC$

$\Rightarrow BG=2GD$.

Suy ra $BG=GM$.

Chứng minh tương tự ta được $CG=GN$.

b) Xét tam giác $GMN$ và tam giác $GBC$ có $GM=GB$ (chứng minh trên);

MGN^=BGC^MGN=BGC (hai góc đối đỉnh);

$GN=GC$ (chứng minh trên).

Do đó $△GMN=△GBC$ (c.g.c)

$\Rightarrow MN=BC$ (hai cạnh tương ứng).

Theo chứng minh trên △GMN=△GBC⇒NMG^=CBG^△GMN=△GBC⇒NMG=CBG (hai góc tương ứng).

Mà NMG^NMG và CBG^CBG ờ vị trí so le trong nên $MN$ // $BC$.

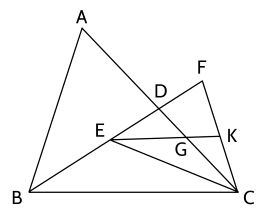
a) Ta có $BF=2BE\Rightarrow BE=EF$.

Mà $BE=2ED$ nên $EF=2ED\Rightarrow D$ là trung điểm của $EF\Rightarrow CD$ là đường trung tuyến của tam giác $EFC$.

Vì $K$ là trung điểm của $CF$ nên $EK$ là đường trung tuyến của $△EFC$.

$△EFC$ có hai đường trung tuyến $CD$ và $EK$ cắt nhau tại $G$ nên $G$ là trọng tâm của $△EFC$.

b) Ta có $G$ là trọng tâm tam giác $EFC$ nên GCDC=23DCGC​=32​ và GE=23EKGE=32​EK

⇒GK=13EK⇒GE=2GK⇒GEGK=2⇒GK=31​EK⇒GE=2GK⇒GKGE​=2.

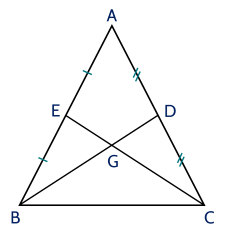
a) Ta có $△ABC$ cân tại $A\Rightarrow AB=AC$ mà $AB=2BE$; $AC=2CD$ (vì $E,D$ theo thứ tự là trung điểm của $AB$, $AC)$.

Do đó ta có $2BE=2CD$ hay $BE=CD$.

Xét $△BCE$ và $△CBD$ có $BE=CD$ (chứng minh trên);

EBC^=DCB^EBC=DCB;

$BC$ là cạnh chung.

Do đó $△BCE=△CBD$ (c.g.c)

$\Rightarrow CE=BD$ (hai cạnh tương ứng).

b) Ta có $G$ là trọng tâm tam giác $ABC$ nên BG=23BDBG=32​BD và CG=23CECG=32​CE (tính chất trọng tâm).

Mà $CE=BD$ (phần a) nên 23CE=23BD32​CE=32​BD hay $CG=BG$.

Vậy tam giác $GBC$ cân tại $G$.

c) Ta có GB=23BD⇒GD=13BD⇒GB=2GD⇒GD=12GBGB=32​BD⇒GD=31​BD⇒GB=2GD⇒GD=21​GB

Chứng minh tương tự, ta có GE=12GCGE=21​GC.

Do đó GD+GE=12GB+12GC=12(GB+GC)GD+GE=21​GB+21​GC=21​(GB+GC).

Mà $GB+GC>BC$ (trong một tam giác tổng độ dài hai cạnh lớn hơn cạnh còn lại).

Do đó GD+GE>12BCGD+GE>21​BC (điều phải chứng minh).

Xét tam giác $ABC$ có hai đường trung tuyến $BM$ và $CN$ cắt nhau tại $G$.

Suy ra $G$ là trọng tâm tam giác $ABC$

⇒BG=23BM⇒BG=32​BM; CG=23CNCG=32​CN

⇒BM=32BG⇒BM=23​BG; CN=32CGCN=23​CG.

Do đó ta phải chứng minh 32BG+32CG>32BC23​BG+23​CG>23​BC hay $BG+CG>BC$. (1)

Bất đẳng thức (1) luôn đúng vì trong một tam giác tổng độ dài hai cạnh lớn hơn độ dài cạnh còn lại.

Vậy BM+CN>32BCBM+CN>23​BC. (điều phải chứng minh).

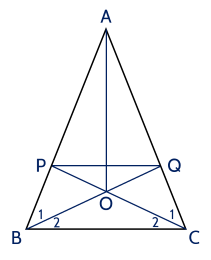
a) $△ABC$ cân tại $A$ nên ABC^=ACB^ABC=ACB.

Vì $BQ$ và $CP$ là đường phân giác của B^,C^B,C nên B1^=B2^=ABC^2B1​​=B2​​=2ABC​, C1^=C2^=ACB^2C1​​=C2​​=2ACB​.

Do đó B1^=B2^=C1^=C2^B1​​=B2​​=C1​​=C2​​.

Suy ra $△OBC$ cân tại $O$.

b) Vì $O$ là giao điểm các đường phân giác $CP$ và $BQ$ trong $△ABC$ nên $O$ là giao điểm ba đường phân giác trong $△ABC$.

Do đó, $O$ cách đều ba cạnh $AB,AC$ và $BC$.

c) Ta có $△ABC$ cân tại $A,AO$ là đường phân giác của góc $A$ nên $AO$ đồng thời là trung tuyến và đường cao của $△ABC$.

Vậy đường thẳng $AO$ đi qua trung điểm của đoạn thẳng $BC$ và vuông góc với nó.

d) Ta có $△PBC=△QCB$ (g.c.g)

$\Rightarrow CP=BQ$ (hai cạnh tương ứng).

e) Ta có $AP=AB-BP$, $AQ=AC-CQ$ (1);

$△PBC=△QCB\Rightarrow BP=CQ$ (2).

Lại có $AB=AC$ (tam giác $ABC$ cân tại $A$) (3).

Từ (1), (2) và (3) suy ra $AP=AQ$.

Vậy tam giác $APQ$ cân tại $A$.

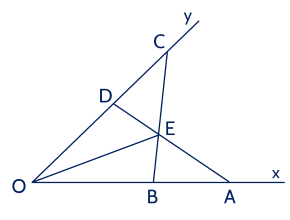
a) Xét $△OAD$ và $△OCB$, có

$OA=OC$ (giả thiết);

O^O chung;

$OD=OB$ (giả thiết).

Do đó $△OAD=△OCB$ (c.g.c)

$\Rightarrow AD=CB$ (hai cạnh tương ứng).

b) Do $OA=OC$ và $OB=OD$ nên $AB=CD$.

Mà $△OAD=△OCB$ (chứng minh trên)

⇒OBC^=ODA^⇒OBC=ODA; OAD^=OCB^OAD=OCB (hai góc tương ứng)

Mặt khác ABE^+OBC^=CDE^+ODA^=180∘ABE+OBC=CDE+ODA=180∘

⇒ABE^=CDE^⇒ABE=CDE

Xét $△ABE$ và $△CDE$ có

OAD^=OCB^OAD=OCB (chứng minh trên);

$AB=CD$ (chứng minh trên);

ABE^=CDE^ABE=CDE (chứng minh trên) 

Do đó $△ABE=△CDE$ (g.c.g).

c) Vi $△ABE=△CDE$ (chứng minh trên) nên $AE=CE$ (hai cạnh tương ứng).

Xét $△AEO$ và $△CEO$ có $AE=CE$ (chứng minh trên);

$OE$ cạnh chung;

$OA=OC$ (giả thiết).

Do đó $△AEO=△CEO$ (c.c.c)

⇒AOE^=COE^⇒AOE=COE (hai góc tương ứng)

$\Rightarrow OE$ là tia phân giác của xOy^xOy​.

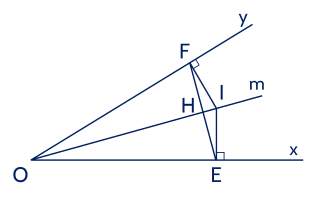
a) Xét $△IOE$ và $△IOF$ có

E^=F^=90∘E=F=90∘ (giả thiết);

$OI$ cạnh chung;

EOI^=FOI^EOI=FOI ($Om$ là tia phân giác).

Vậy $△IOE=△IOF$ (cạnh huyền - góc nhọn).

b) $△IOE=△IOF$ (chứng minh trên)

$\Rightarrow OE=OF$ (hai cạnh tương ứng).

Gọi $H$ là giao điểm của $Om$ và $EF$.

Xét $△OHE$ và $△OHF$, có

$OE=OF$ (chứng minh trên);

EOH^=FOH^EOH=FOH ($Om$ là tia phân giác);

$\mathrm{OH}$ chung.

Do đó $△OHE=△OHF$ (c.g.c)

⇒OHE^=FHO^⇒OHE=FHO (hai góc tương ứng)

Mà OHE^+FHO^=180∘OHE+FHO=180∘ nên OHE^=FHO^=90∘OHE=FHO=90∘.

Vậy $EF\perp Om$.

Kẻ $IE\perp AD$ (với $E\in AD$).

Gọi $Ax$ là tia đối của tia $AB$.

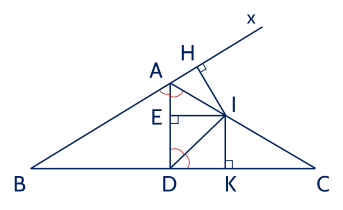
Vì BAC^BAC và CAx^CAx là hai góc kề bù mà BAC^=120∘BAC=120∘ nên CAx^=60∘CAx=60∘ (1) 

Ta có $AD$ là phân giác của BAC^⇒DAC^=12BAC^=60∘BAC⇒DAC=21​BAC=60∘ (2)

Từ (1) và (2) suy ra $AC$ là tia phân giác của DAx^DAx

$\Rightarrow IH=IE$ (tính chất tia phân giác của một góc) (3)

Vì $DI$ là phân giác của ADC^ADC nên $IK=IE$ (tính chất tia phân giác của một góc) (4)

Từ (3) và $(4)$ suy ra $IH=IK$.

Ta có $D$ thuộc phân giác của A^A;

$DH\perp AB$; $DK\perp AC$ $\Rightarrow DH=DK$ (tính chất tia phân giác của một góc).

Gọi $G$ là trung điểm của $BC$.

Xét $△BGD$ và $△CGD$, có

BGD^=CGD^=90∘BGD=CGD=90∘ ($DG$ là trung trực của $BC$ ),

$BG=CG$ (già thiết),

$DG$ là cạnh chung.

Do đó $△BGD=△CGD$ (hai cạnh góc vuông)

$\Rightarrow BD=CD$ (hai cạnh tương ứng).

Xét $△BHD$ và $△CKD$, có

BHD^=CKD^=90∘BHD=CKD=90∘ (giả thiết);

$DH=DK$ (chứng minh trên);

$BD=CD$ (chứng minh trên).

Do đó $△BHD=△CKD$ (cạnh huyền - cạnh góc vuông)

$\Rightarrow BH=CK$ (hai cạnh tương ứng).