

Bùi Hà Chi
Giới thiệu về bản thân



































a) Ta có suy ra nên và //
Do đó, là hình bình hành.
Lại có nên là hình thoi
b) // suy ra là hình thang.
Mà mà là phân giác nên .
Vậy là hình thang cân.
c) có nên là tam giác cân.
Xét và có:
(giả thiết)
(đối đỉnh)
(so le trong)
Vậy (g.c.g) suy ra (hai cạnh tương ứng).
Khi đó là đường trung tuyến và (hai cạnh tương ứng)
Mà suy ra hay là đường trung tuyến.
Khi đó, có ba đường trung tuyến đồng quy.
Bạn chưa trả lời câu hỏi này. Trả lời câu hỏi này Bài 3 Xem hướng dẫn Bình luận (16)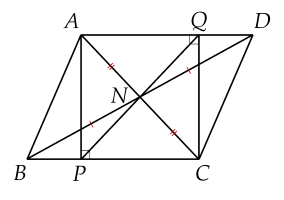
Cho nhọn có Gọi là trung điểm của Lấy điểm trên tia sao cho
a) Chứng minh là hình bình hành.
b) Kẻ Chứng minh thẳng hàng.
c) cần thêm điều kiện gì để tứ giác là hình vuông.
a) Ta có suy ra nên và //
Do đó, là hình bình hành.
Lại có nên là hình thoi
b) // suy ra là hình thang.
Mà mà là phân giác nên .
Vậy là hình thang cân.
c) có nên là tam giác cân.
Xét và có:
(giả thiết)
(đối đỉnh)
(so le trong)
Vậy (g.c.g) suy ra (hai cạnh tương ứng).
Khi đó là đường trung tuyến và (hai cạnh tương ứng)
Mà suy ra hay là đường trung tuyến.
Khi đó, có ba đường trung tuyến đồng quy.
Bạn chưa trả lời câu hỏi này. Trả lời câu hỏi này Bài 3 Xem hướng dẫn Bình luận (16)
Cho nhọn có Gọi là trung điểm của Lấy điểm trên tia sao cho
a) Chứng minh là hình bình hành.
b) Kẻ Chứng minh thẳng hàng.
c) cần thêm điều kiện gì để tứ giác là hình vuông.
a) Ta có và suy ra .
Mặt khác .
Xét và có
( giả thiết)
(chứng minh trên)
Suy ra (g.c.g)
b) Từ suy ra (hai cạnh tương ứng)
Chứng minh tương tự cho và
Suy ra và .
Khi đó
a) Ta có và suy ra .
Mặt khác .
Xét và có
( giả thiết)
(chứng minh trên)
Suy ra (g.c.g)
b) Từ suy ra (hai cạnh tương ứng)
Chứng minh tương tự cho và
Suy ra và .
Khi đó
ko bt
ko bt
a) Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên là hình bình hành.
vuông tại có là đường trung tuyến nên .
Vậy hình bình hành có nên là hình thoi.
b) Vì là hình thoi nên // và .
Tứ giác có // nên là hình bình hành.
c) Để là hình vuông thì cần có một góc vuông hay .
Khi đó có vừa là đường cao vừa là đường trung tuyến nên cân tại .
Vậy vuông cân tại thì là hình vuông.
Cho vuông cân tại . Trên cạnh lấy hai điểm sao cho Qua và kẻ các đường thẳng vuông góc với chúng cắt lần lượt tại
a) Chứng minh là tam giác vuông cân.
b) Chứng minh tứ giác là hình vuông.
Hướng dẫn giải:a) vuông cân nên
vuông tại có
Suy ra nên .
Vậy vuông cân tại
b) Chứng minh tương tự câu a ta được vuông cân tại nên và
Mặt khác suy ra và // (cùng vuông góc với
Tứ giác có // nên là hình bình hành.
Hình bình hành có một góc vuông nên là hình chữ nhật
Hình chữ nhật có hai cạnh kề bằng nhau nên là hình vuông.
Tứ giác có ba góc vuông
Nên là hình chữ nhật.
Mà nằm trên tia phân giác suy ra .
Khi đó là hình vuông
ko bt