

when the imposter is sus
Giới thiệu về bản thân



































đề không rõ ràng, vẽ xong thì thấy sai đề, chơi thế ai chơi lại
Từ tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{3x+2}{3}=\dfrac{2y-6}{9}=\dfrac{\left(3x+2\right)+\left(2y-6\right)}{3+9}=\dfrac{3x+2y-4}{12}=\dfrac{3x+2y-4}{6x}\)
Suy ra 6x = 12 <=> x = 12 : 6 = 2
Khi đó \(\dfrac{3x+2}{3}=\dfrac{3\cdot2+2}{3}=\dfrac{8}{3}\)
Suy ra \(\dfrac{2y-6}{9}=\dfrac{8}{3}\Leftrightarrow2y-6=\dfrac{8\cdot9}{3}=24\)
\(\Leftrightarrow2y=24+6=30\Leftrightarrow y=30:2=15\)
Vậy x = 2; y = 15
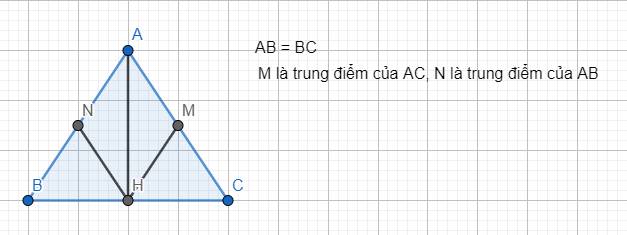
a) Xét hai tam giác ABH và ACH ta có:
- AB = AC (vì ABC là tam giác cân)
- HB = HC (vì H là trung điểm của BC)
- \(\widehat{B}=\widehat{C}\) (vì ABC là tam giác cân)
Vậy \(\Delta ABH=\Delta ACH\) (c.g.c)
b) Xét hai tam giác NBH và MCH ta có:
- NB = MC (vì AB = AC, M là trung điểm của AC và N là trung điểm của AB)
- HB = HC (đã chứng minh trên)
- \(\widehat{B}=\widehat{C}\) (đã chứng minh trên)
Suy ra \(\Delta NBH=\Delta MCH\) (c.g.c)
Khi đó HN = HM (vì hai cạnh tương ứng)
Gọi số học sinh khối 6; 7; 8 của trường đó lần lượt là x; y; z (học sinh).
Theo đề, ta có x + y + z = 441
Và \(\left(1-\dfrac{1}{3}\right)x=\left(1-\dfrac{1}{4}\right)y=\left(1-\dfrac{1}{5}\right)z\)
Suy ra \(\dfrac{2}{3}x=\dfrac{3}{4}y=\dfrac{4}{5}z\) hay \(\dfrac{x}{\dfrac{3}{2}}=\dfrac{y}{\dfrac{4}{3}}=\dfrac{z}{\dfrac{5}{4}}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{\dfrac{3}{2}}=\dfrac{y}{\dfrac{4}{3}}=\dfrac{z}{\dfrac{5}{4}}=\dfrac{x+y+z}{\dfrac{3}{2}+\dfrac{4}{3}+\dfrac{5}{4}}=\dfrac{441}{\dfrac{49}{12}}=108\)
Suy ra \(x=108\cdot\dfrac{3}{2}=162;y=108\cdot\dfrac{4}{3}=144;z=108\cdot\dfrac{5}{4}=135\)
Vậy số học sinh của mỗi khối lần lượt là 162 học sinh, 144 học sinh & 135 học sinh
Theo đề ta có:
\(\overline{2023a}⋮2022\) (với a có n chữ số, \(n\inℕ^∗\))
\(\Leftrightarrow\left(2023\cdot10^n+a\right)⋮2022\)
Vì \(2023\equiv1\left(mod2022\right)\Leftrightarrow2023\cdot10^n+a\equiv10^n+a\left(mod2022\right)\)
Mà \(\overline{2023a}⋮2022\Rightarrow\left(10^n+a\right)⋮2022\)
Xét \(a⋮2022\). Vì \(\left(10^n+a\right)⋮2022\) nên \(10^n⋮2022\) (không có nghiệm).
Khi đó \(a⋮̸2022\). Đặt x sao cho \(a\equiv x\left(mod2022\right)\).
Suy ra \(10^n\equiv2022-x\left(mod2022\right)\)
Ta có bảng sau:
| n | 1 | 2 | 3 | 4 | 5 | ... |
| 2022 - x | 10 | 100 | 1000 | 1912 | 922 | ... |
| x | 2012 | 1922 | 1022 | 110 | 1100 | ... |
| Min(a) > 10n | Không có | Không có | Không có | 2132 | 11210 | ... |
| Chọn hay loại? | Loại | Loại | Loại | Chọn | Loại | ... |
Vậy số tự nhiên a cần tìm là 2132.
P/s: bài này có vẻ không phải lớp 7!!!
Bài 5: Ta có bảng:
| Đa thức | \(f\left(x\right)=5x^2-7+6x-8x^3-x^4\) | \(g\left(x\right)=x^4+5+8x^3-5x^2\) |
| Được sắp xếp | \(-x^4-8x^3+5x^2+6x-7\) | \(x^4+8x^3-5x^2+5\) |
| Bậc | 4 | 4 |
| HSCN | -1 | 1 |
| HSTD | -7 | 5 |
(HSCN: hệ số cao nhất, HSTD: hệ số tự do)
b)\(f\left(x\right)+g\left(x\right)=\left(5x^2-7+6x-8x^3-x^4\right)+\left(x^4+5+8x^3-5x^2\right)=6x-2\)
\(f\left(x\right)-g\left(x\right)=\left(5x^2-7+6x-8x^3-x^4\right)-\left(x^4+5+8x^3-5x^2\right)=-2x^4-16x^3+10x^2+6x-12\)
c) Ta có \(P\left(x\right)=f\left(x\right)+g\left(x\right)=6x-2\)
Vì \(\left|x\right|=1\) nên \(x=\pm1\)
Ta có bảng:
| \(x\) | 1 | -1 |
| \(6x-2\) | 4 | -8 |
Vậy P(x) = 4 hoặc -8 khi |x| = 1
Bài 6:
a) Sai đề: f(-1) bằng bao nhiêu???
b) Khi P(0) = 4 suy ra c = 4
Khi P(1) = 7 suy ra a + b + c = 7 <=> a + b = 7 - 4 = 3
Khi P(-1) = 10 suy ra a - b + c = 10 <=> a - b = 10 - 4 = 6
Từ đó suy ra 2a = (a + b) + (a - b) = 3 + 6 = 9 <=> a = 9/2 = 4,5
Suy ra b = 3 - 4,5 = -1,5
Vậy a = 4,5; b = -1,5; c = 4
Bài 7: Ta có:
\(-1001x^7=-1000x^7-x^7\)
\(1001x^6=1000x^6+x^6\)
...
\(-1001x=-1000x-x\)
Suy ra \(P\left(x\right)=x^8-1000x^7-x^7+1000x^6+x^6-...-1000x-x+250\)
\(P\left(x\right)=x^7\left(x-1000\right)-x^6\left(x-1000\right)+x^5\left(x-1000\right)-...+x\left(x-1000\right)-x+250\)
Đặt x = 1000 ta được:
\(P\left(x\right)=-1000+250=-750\)
Biện luận trước khi giải: \(a,b\inℕ^∗\). Khi a hoặc b bằng 0 thì biểu thức không xác định.
Bài làm:
Ta có \(1+2+3+...+a=\dfrac{a\left(a+1\right)}{2}\)
Và \(1+2+3+...+b=\dfrac{b\left(b+1\right)}{2}\)
Suy ra \(\dfrac{a\left(a+1\right)}{2a}< \dfrac{b\left(b+1\right)}{2b}\) <=> \(\dfrac{a+1}{2}< \dfrac{b+1}{2}\)
<=> \(a+1< b+1\) <=> a < b
Trước hết ta có \(\left(\dfrac{x}{y}\right)^{-z}=\dfrac{1}{\left(\dfrac{x}{y}\right)^z}=\dfrac{1}{\dfrac{x^z}{y^z}}=\dfrac{y^z}{x^z}\)
Suy ra:
\(A=\left(0,25\right)^{-1}\cdot\left(\dfrac{1}{4}\right)^{-2}\cdot\left(\dfrac{4}{3}\right)^{-2}\cdot\left(\dfrac{5}{4}\right)^{-1}\cdot\left(\dfrac{2}{3}\right)^{-3}\)
\(A=\left(\dfrac{1}{4}\right)^{-1}\cdot\left(\dfrac{1}{4}\right)^{-2}\cdot\left(\dfrac{4}{3}\right)^{-2}\cdot\left(\dfrac{5}{4}\right)^{-1}\cdot\left(\dfrac{2}{3}\right)^{-3}\)
\(A=4\cdot4^2\cdot\dfrac{3^2}{4^2}\cdot\dfrac{4}{5}\cdot\dfrac{3^3}{2^3}=4^2\cdot3^5\text{}\div5\div2^3\)
\(A=2^4\div2^3\cdot3^5\div5=2\cdot3^5\div5=2\cdot243\div5=\dfrac{486}{5}\)
\(1+\dfrac{1}{2}\left(1+2\right)+\dfrac{1}{3}\left(1+2+3\right)+...+\dfrac{1}{20}\left(1+2+...+20\right)\)
\(=1+\dfrac{3\cdot2\div2}{2}+\dfrac{4\cdot3\div2}{3}+...+\dfrac{21\cdot20\div2}{20}\)
\(=1+\dfrac{3}{2}+2+...+\dfrac{21}{2}\) (A)
Trong (A) có \(\dfrac{\dfrac{21}{2}-1}{\dfrac{3}{2}-1}+1=20\) (số hạng)
Suy ra \(\left(A\right)=\left(\dfrac{21}{2}+1\right)\cdot20\div2=115\)
Vậy \(1+\dfrac{1}{2}\left(1+2\right)+\dfrac{1}{3}\left(1+2+3\right)+...+\dfrac{1}{20}\left(1+2+...+20\right)=115\)