10 050 704

Tuổi con hiện nay:

  42 : 7 = 6 (tuổi)

Hiệu số tuổi hai mẹ con:

  42 - 6 = 36 (tuổi)

Vì hiệu số tuổi hai mẹ con luôn không đổi

Nên khi tuổi mẹ gấp 4 lần tuổi con thì hiệu số tuổi hai mẹ con vẫn là 36 tuổi

Coi tuổi mẹ khi đó 4 phần và tuổi con khi đó 1 phần

Hiệu số phần bằng nhau:

  4 - 1 = 3 (phần)

Tuổi con khi đó là:

  36 : 3 = 12 (tuổi)

Sau số năm nữa thì tuổi mẹ gấp 4 lần tuổi con là:

  12 - 6 = 6 (năm)

   Đáp số: 6 năm

Hoàn thiện phép tính:

\(164-16=148\)

\(\overline{ab4}-\overline{ab}=\overline{a48}\\\overline{ab0}+4-\overline{ab}=\overline{a00}+48\\ \overline{ab}\times10-\overline{ab}=\overline{a00}+48-4\\ \overline{ab}\times9=\overline{a44} \) (*)

Để tìm được \(\overline{ab}\) là STN có 2 chữ số, hiển nhiên \(\overline{a44}\) phải chia hết cho 9

Suy ra: a + 4 + 4 cũng phải chia hết cho 9

hay a + 8 chia hết cho 9

Mà a là số có 1 chữ số nên a = 1

Thay vào biểu thức (*) :

\(\overline{1b}\times9=144\\ \overline{1b}=144:9\\ \overline{1b}=16\\ b=6\) (nhận)

Vậy: a=1 và b=6 hay \(\overline{ab}=16\)

Dễ dàng so sánh được:

\(-\dfrac{5}{3}< -\dfrac{3}{3}=-1=-\dfrac{5}{5}< -\dfrac{4}{5}< 0< \dfrac{1}{3}< \dfrac{5}{3}< \dfrac{6}{3}=2=\dfrac{4}{2}< \dfrac{7}{2}\)

Vẽ trục số:

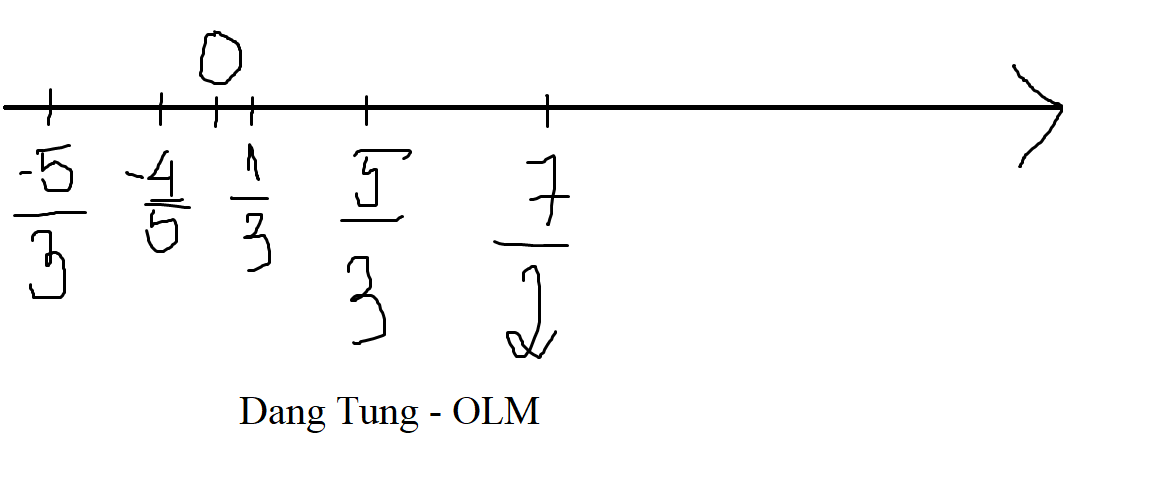
a) 733 - (33 + 320)

= 733 - 33 - 320

= 700 - 320

= 380

b) 945 + (372 - 245)

= 945 + 372 - 245

= (945 - 245) + 372

= 700 + 372

= 1072

c) 717 - (617 - 225)

= 717 - 617 + 225

= 100 + 225 

= 325

d) 1732 - (732 - 257)

= 1732 - 732 + 257

= 1000 + 257

= 1257

P = (a - b) - (b - c + a) - c

= a - b - b + c - a - c

= ( a - a ) + ( -b - b) + ( c - c )

= -2b

=> Đáp án B

Câu 8:

a) -13,1

456,6

-8865,1

66,7

b) -13

457

-8865

67

c) -13,15

456,58

-8865,12

66,66

Câu 9:

\(\dfrac{3}{10}=\dfrac{30}{100}=30\%\\ \dfrac{4}{5}=\dfrac{80}{100}=80\%\\ \dfrac{30}{8}=\dfrac{15}{4}=\dfrac{375}{100}=375\%\)

Thời gian đi từ A đến B của ô tô là:

   72 : 48 = 1,5 (giờ) = 1 giờ 30 phút

Ô tô đến B lúc:

  7 giờ + 1 giờ 30 phút = 8 giờ 30 phút

  Đáp số: 8 giờ 30 phút

\(A=\dfrac{6n-1}{2n+3}=\dfrac{3\left(2n+3\right)-10}{2n+3}\\ =3-\dfrac{10}{2n+3}\)

Để A nguyên thì: \(\dfrac{10}{2n+3}\) nguyên

\(\Rightarrow10⋮\left(2n+3\right)\)

\(\Rightarrow2n+3\inƯ\left(10\right)=\left\{1;-1;2;-2;5;-5;10;-10\right\}\\ \Rightarrow2n\in\left\{-2;-4;-1;-5;2;-8;7;-13\right\}\\ \Rightarrow n\in\left\{-1;-2;-\dfrac{1}{2};-\dfrac{5}{2};1;-4;\dfrac{7}{2};-\dfrac{13}{2}\right\}\)