

Nguyễn Thị Ái Vân
Giới thiệu về bản thân



































Bổ sung câu 1.
Các thành phần của tế bào nhân sơ:
- 1 - Roi
- 2 - Lông
- 3 - Thành tế bào
- 4 - Màng tế bào
- 5 - Ribosome
- 6 - Vùng
1.
2. Vì kích thước nhỏ nên tỉ lệ S/V lớn, từ đó tế bào nhân sơ sinh trưởng và sinh sản nhanh
1.
2. Vì kích thước nhỏ nên tỉ lệ S/V lớn, từ đó tế bào nhân sơ sinh trưởng và sinh sản nhanh
vtb=\(-\frac{\Delta\left\lbrack NOCl\right\rbrack}{2\Delta t}\) = \(\frac{\Delta\left\lbrack NO\right\rbrack}{2\Delta t}\) =\(\frac{\Delta\left\lbrack Cl2\right\rbrack}{\Delta t}\)
P(Z = 15): 1s2 2s2 2p6 3s2 3p3 -> P cần thêm 3 electron để đạt octet
H(Z = 1): 1s1 -> H cần thêm 1 electron để đạt octet
Khi hình thành liên kết, P góp chung 3 electron với 3 electron của 3 H ⇒ Trong PH3, xung quanh P có 8 electron giống khí hiếm Ar còn 3 H đều có 2 electron giống khí hiếm He.
Không có khả năng hút hết
a/ 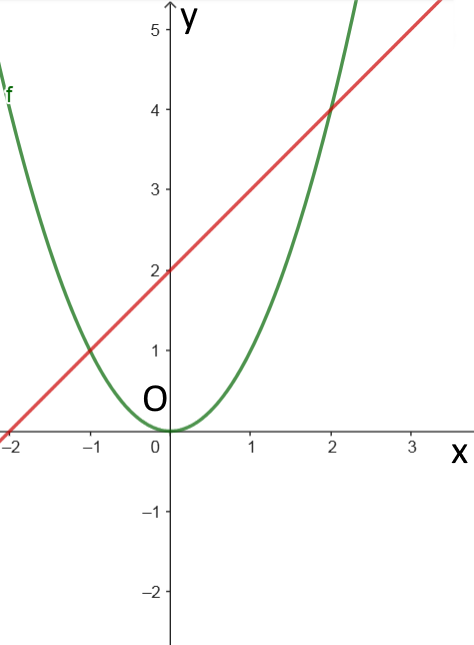
b/ \(x^2-x-2=0\)
ac = 1.(-2) = -2 < 0 --> PT có 2 nghiệm phân biệt
\(\Delta=b^2-4ac=\left(-1\right)^2-4\cdot1\cdot\left(-2\right)=9\)
\(x_1=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{-\left(-1\right)+\sqrt{9}}{2\cdot1}=2\)
\(x_2=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{-\left(-1\right)-\sqrt{9}}{2\cdot1}=-1\)
Vậy: giao điểm của (P) và (d) lần lượt là (2;4) và (-1;1)
Subject: Changes in My Family Hi Hoai, I hope this email finds you well. I wanted to share some recent changes in my family. My sister just started university, and we’re all very proud of her. She’s studying engineering and seems to enjoy it a lot. Meanwhile, my dad got a new job closer to home, so we get to spend more time together, which has been wonderful. My mom has also taken up gardening, and our backyard is now full of beautiful flowers and vegetables. These changes have brought us closer as a family, and I feel really happy about it. How about you? Any updates on your side? Looking forward to hearing from you soon! Best wishes, Dien
Subject: Changes in My Family
Hi H
I hope this email finds you well. I wanted to share some recent changes in my family. My sister just started university, and we’re all very proud of her. She’s studying engineering and seems to enjoy it a lot. Meanwhile, my dad got a new job closer to home, so we get to spend more time together, which has been wonderful. My mom has also taken up gardening, and our backyard is now full of beautiful flowers and vegetables.
These changes have brought us closer as a family, and I feel really happy about it. How about you? Any updates on your side?
Looking forward to hearing from you soon!
Best wishes,
Dien
1. This is the first time I have made mooncakes for the Mid - Autumn Festival. 2. I had a desire to explore the hidden gems of the city that most tourists miss. 3. Bao wishes he had a big house.