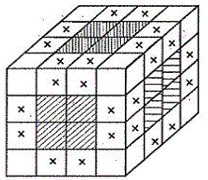
a) Ở mỗi mặt, có \(4\) hình lập phương nhỏ được sơn một mặt (các hình được gạch sọc).

Ở sáu mặt có: \(4.6 \&\text{nbsp}; = 24\) (hình).

b) Ở mỗi cạnh, có \(2\) hình lập phương được sơn hai mặt (các hình ghi dấu "\(x\)").

Ở \(12\) cạnh có : \(2.12 = 24\) (hình).

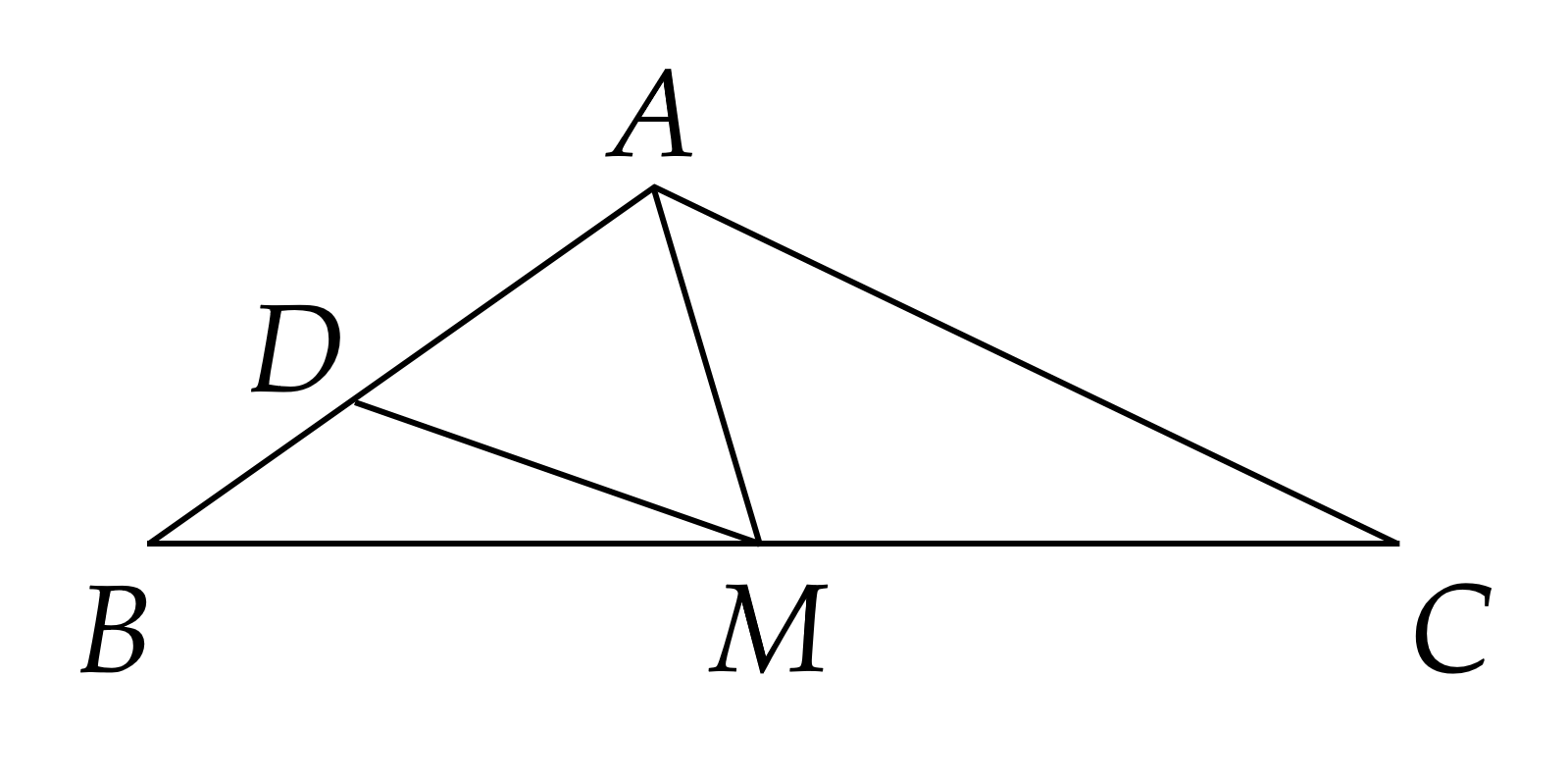
Ta có: \(A B = A D + D B\)

Suy ra \(D B = A B - A D = 10 - 6 = 4\) cm

\(A M\) là trung tuyến của \(\Delta A B C\) suy ra \(M\) là trung điểm của \(B C\)

Suy ra \(B M = C M = \frac{1}{2} B C = 15\) cm.

 Xét \(\Delta A B M\) có \(M D\) là phân giác của góc \(A M B\) nên

\(\frac{A M}{B M} = \frac{A D}{D B}\)

\(\frac{A M}{B M} = \frac{6}{4} = \frac{3}{2}\)

Do đó \(A M = \frac{3}{2} . B M = \frac{3}{2} . 15 = 22 , 5\) (cm).

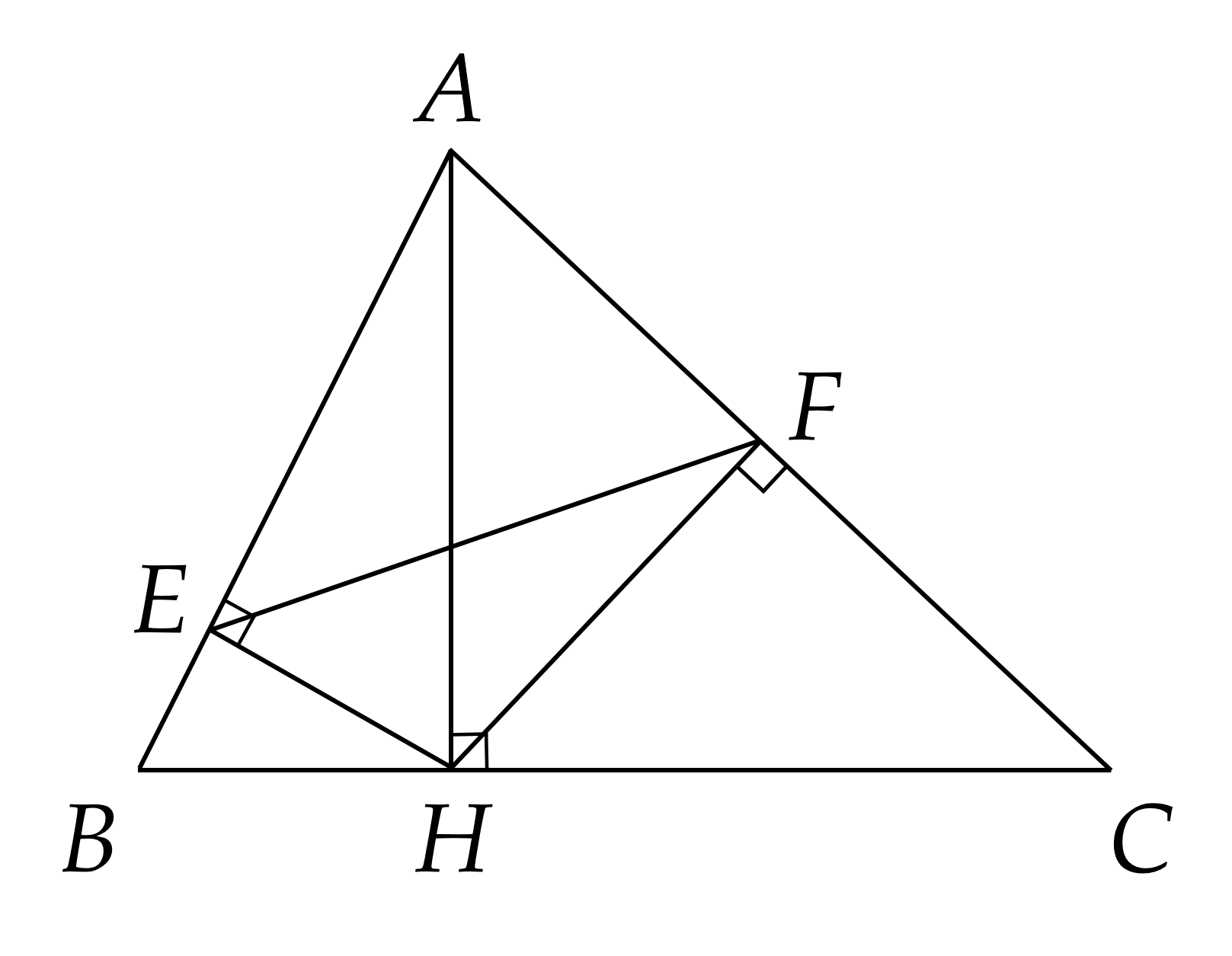
a) Xét \(\Delta A E H\) và \(\Delta A H B\) có:

\(\hat{B A H}\) chung và \(\hat{A E H} = \hat{A H B} = 9 0^{\circ}\)

Do đó \(\Delta A E H \sim \Delta A H B\) (g.g)

Suy ra \(\frac{A H}{A B} = \frac{A E}{A H}\) hay \(A H^{2} = A E . A B\) (1)

b) Chứng minh tương tự \(\Delta A H F \sim \Delta A C H\) (g.g) 

Suy ra \(\frac{A H}{A C} = \frac{A F}{A H}\) hay \(A H^{2} = A F . A C\) (2)

Từ (1) và (2) suy ra \(A E . A B = A F . A C\)

c) Ta có \(A E . A B = A F . A C\) nên \(\frac{A E}{A C} = \frac{A F}{A B}\).

Xét \(\Delta A E F\) và \(\Delta A C B\) có:

\(\hat{E A F}\) chung

\(\frac{A E}{A C} = \frac{A F}{A B}\) (cmt)

Do đó \(\Delta A E F \&\text{nbsp}; \sim \Delta A C B\) (c.g.c).

Suy ra \(\frac{E F}{C B} = \frac{P_{A E F}}{P_{A C B}} = \frac{20}{30} = \frac{2}{3}\) (tỉ số chu vi bằng tỉ số đồng dạng)

Áp dụng tính chất dãy tỉ số bằng nhau ta có \(\frac{S_{A E F}}{4} = \frac{S_{A C B}}{9} = \frac{S_{A C B} - S_{A E F}}{9 - 4} = \frac{25}{5} = 5\)

Suy ra

\(S_{A E F} = 5.4 = 20\) cm\(^{2}\);

\(S_{A C B} = 5.9 = 45\) cm\(^{2}\).

Vậy \(S_{A E F} = 20\) cm\(^{2}\) và \(S_{A C B} = 45\) cm\(^{2}\).

Xác suất cho biến cố "Thẻ rút ra là thẻ đánh số 3" là: \(\frac{6}{20} = \frac{3}{10}\).

Gọi vận tốc riêng của ca nô là \(x\) (km/h, \(x > 3\)).

Vận tốc ca nô khi đi xuôi khúc sông từ \(A\) đến \(B\) là: \(x + 3\) (km/h);

Vận tốc ca nô khi đi ngược khúc sông từ \(B\) về \(A\) là: \(x - 3\) (km/h);

Khúc sông \(A B\) có chiều dài không đổi nên ta có phương trình: \(\frac{3}{2} \left(\right. x + 3 \left.\right) = 2 \left(\right. x - 3 \left.\right)\).

Giải phương trình trên ta nhận được \(x = 21\) (thỏa mãn)

Do đó vận tốc riêng của ca nô là \(21\) km/h.

Chiều dài khúc sông là: \(2 \left(\right. 21 - 3 \left.\right) = 36\) (km).

Vậy vận tốc riêng của cano là \(21\) km/h, chiều dài khúc sông là \(36\) km .

a) 3x - x = 5 + 4

2x = 9

x = \(\frac92\)

Vậy nghiệm của phương trình là x=\(\frac92\)

b) 3x - 3 - 7 = 5x + 10

3x -5x = 3 + 7 + 10

-2x = 20

x = -10

Vậy nghiệm của phương trình là x=-10

Go Green Club

NOTICE

12 January, 2024

Lecture on Water Pollution

Our Go Green Club is organising a lecture about Water pollution - one of the most serious problems in the world at the moment. Students from all the classes can participate in. If you are interested in our lecture, contact us by 22 January, 2024.

Lecture details:

Time: 2 p.m - 4 p.m., 6 March

Place: School Grand Hall

Topic: Water Pollution

If you have any questions, please contact us at 0936.120.169 or email at hotro@vietjack.com.

Club Leader,

Nguyen Hong Mai

191