Do \(A\) là trung điểm \(O B\), nên \(O B = 2. O A\).

Thay số \(O A = 2\) cm, ta có

\(O B = 2.2 = 4\) (cm)

2. (Không yêu cầu vẽ lại hình).

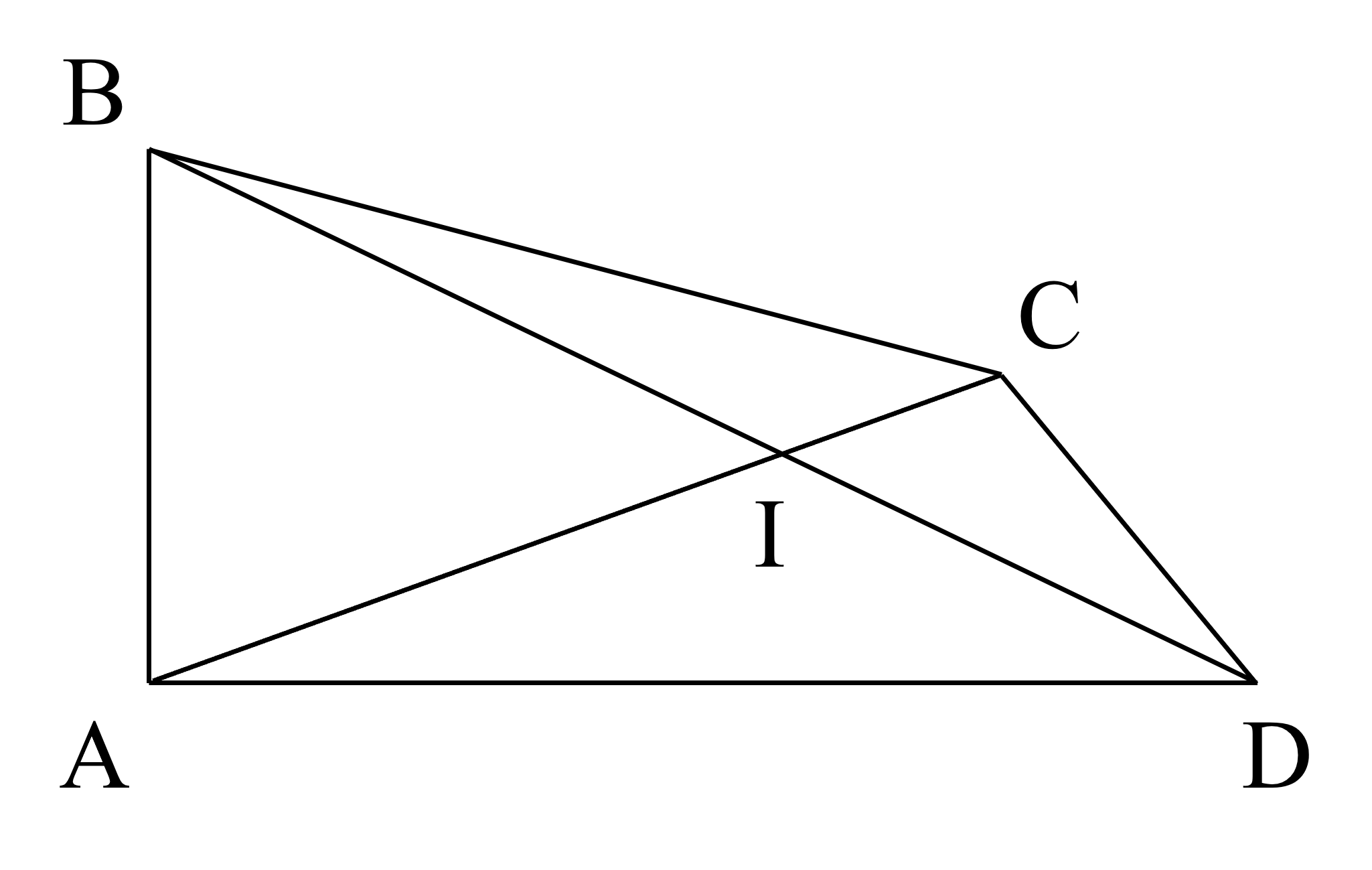
a) Điểm \(C\) và điểm \(I\) nằm trong góc \(B A D\).

b) (Học sinh nêu ra một góc bẹt sẽ đạt điểm tối đa phần này.)

Các góc bẹt trong hình là góc \(B I D\) và \(A I C\).

c) (Không trừ điểm học sinh khi đo góc có sai số từ \(1^{\circ}\) đến \(2^{\circ}\)).

Đo góc, ta lần lượt có các số đo góc như sau:

\(\hat{A I C} = 18 0^{\circ}\)

\(\hat{A C D} = 7 0^{\circ}\)

\(\hat{B C D} = 13 5^{\circ}\)

\(\hat{B A D} = 9 0^{\circ}\)

Sắp xếp các góc theo thứ tự tăng dần về số đo, ta được:

\(\hat{A C D} ; \hat{B A D} ; \hat{B C D} ; \hat{A I C}\).

Số học sinh đạt loại Tốt là:

\(45. \frac{4}{15} = 12\) (học sinh)

Số học sinh đạt loại Khá là:

\(12. \frac{5}{3} = 20\) (học sinh)

Số học sinh được xếp loại Đạt là:

\(45 - 12 - 20 = 13\) (học sinh)

Đáp số: \(13\) học sinh

a) \(\frac{1}{2} - \frac{1}{2} : x = \frac{3}{4}\)

\(\frac{1}{2} : x = \frac{1}{2} - \frac{3}{4}\)

\(\frac{1}{2} : x = \frac{- 1}{4}\)

\(x = \frac{1}{2} : \&\text{nbsp}; \frac{- 1}{4}\)

\(x = - 2\)

b) \(\frac{x - 1}{15} = \frac{3}{5}\)

\(\frac{x - 1}{15} = \frac{9}{15}\)

\(x - 1 = 9\)

\(x = 10\)

c) \(x + 2 , 5 = 1 , 4\)

\(x = 1 , 4 - 2 , 5\)

\(x = - 1 , 1\)

a) \(A = 2 , 34 + 5 , 35 + 7 , 66 + 4 , 65\)

\(= \left(\right. 2 , 34 + 7 , 66 \left.\right) + \left(\right. 4 , 65 + 5 , 35 \left.\right)\)

\(= 10 + 10\)

\(= 20\)

b) \(B = 2 , 13.75 + 2 , 13.25\)

\(= 2 , 13. \left(\right. 75 + 25 \left.\right)\)

\(= 2 , 13.100\)

\(= 213\)

c) \(C = \frac{1}{3} - \frac{1}{3} : \frac{3}{4}\)

\(= \frac{1}{3} - \frac{1}{3} . \&\text{nbsp}; \frac{4}{3}\)

\(= \frac{1}{3} - \frac{4}{9}\)

\(= \frac{3}{9} - \frac{4}{9}\)

\(= \frac{- 1}{9}\)

B=1.44​+4.74​+7.104​+....+94.974​+97.1004​

\(B = 4 \left(\right. \frac{1}{1.4} + \frac{1}{4.7} + \frac{1}{7.10} + . . . . + \frac{1}{94.97} + \frac{1}{97.100} \left.\right)\)

\(B = \frac{4}{3} \left(\right. \frac{3}{1.4} + \frac{3}{4.7} + \frac{3}{7.10} + . . . . + \frac{3}{94.97} + \frac{3}{97.100} \left.\right)\)

\(B = \frac{4}{3} \left(\right. 1 - \frac{1}{4} + \frac{1}{4} - \frac{1}{7} + \frac{1}{7} - \frac{1}{10} + . . . . + \frac{1}{94} - \frac{1}{97} + \frac{1}{97} - \frac{1}{100} \left.\right)\)

\(B = \frac{4}{3} \left(\right. 1 - \frac{1}{100} \left.\right)\)

\(B = \frac{4}{3} . \frac{99}{100}\)

\(B = \frac{33}{25}\).

Vậy \(B = \frac{33}{25}\).

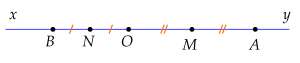
a) Ta có điểm \(M\) nằm giữa \(O\) và \(A\) \(\left(\right. M\) là trung điểm \(O A \left.\right)\) hay \(M\) và \(A\) cùng phía so với \(O\).

Mặt khác \(A\) thuộc tia \(O x\) nên \(M\) thuộc tia \(O x\).

Tương tự, điểm \(N\) nằm giữa \(O\) và \(B\) \(\left(\right. N\) là trung điểm \(O B \left.\right)\) hay \(N\) và \(B\) cùng phía so với \(O\).

Mặt khác \(B\) thuộc tia \(O y\) nên \(N\) thuộc tia \(O y\).

Mà \(O x\) và \(O y\) là hai tia đối nên \(M\) và \(N\) khác phía so với \(O\).

Vậy \(O\) nằm giữa \(M\) và \(N\).

b) Theo đề bài, ta có \(M\) là trung điểm của \(O A\) nên:

\(O M = M A = \frac{O A}{2} = 3\) cm.

Ta có \(N\) là trung điểm của \(O B\) nên:

\(O N = N B = \frac{O B}{2} = \frac{3}{2} = 1 , 5\) cm.

Vì \(O\) nằm giữa điểm \(M\) và \(N\) nên ta có:

\(O M + O N = M N\) hay \(M N = 3 + 1 , 5 = 4 , 5\) cm.

1. Cân nặng của quả dưa hấu là:

\(2 : \frac{2}{3} = 3\) (kg).

Vậy quả dưa hấu nặng \(3\) kg.

2. Số thí sinh Châu Á dự thi là:

\(152. \frac{7}{19} = 56\) (thí sinh)

Số thí sinh Châu Âu, Châu Phi và Châu Mỹ tham gia dự thi là:

\(152 - 56 = 96\) (thí sinh)

Số thí sinh Châu Âu tham gia dự thi là:

\(96. \frac{5}{8} = 60\) (thí sinh)

Số thí sinh Châu Phi và Châu Mỹ dự thi là:

\(96 - 60 = 36\) (thí sinh)

Số thí sinh Châu Mỹ nhiều hơn số thí sinh Châu Phi là \(8\).

Do đó, số thí sinh Châu Mỹ tham gia dự thi là:

\(\left(\right. 36 + 8 \left.\right) : 2 = 22\) (thí sinh)

Số thí sinh Châu Phi dự thi là:

\(22 - 8 = 14\) (thí sinh)

Vậy Châu Á có \(56\) thí sinh, Châu Âu có \(60\) thí sinh, Châu Mỹ có \(22\) thí sinh, Châu Phi có \(14\) thí sinh.

a) Em hãy trình bày khái quát tổ chức chính quyền thời Đinh – Tiền Lê?

* Tổ chức chính quyền thời Đinh:

- Trung ương:

+ Hoàng đế đứng đầu triều đình trung ương.

+ Giúp vua trị nước có các cao tăng và ban văn, ban võ.

+ Tướng lĩnh thân cận giữ chức vụ chủ chốt.

- Địa phương: gồm đạo (châu), giáp, xã.

* Tổ chức chính quyền thời Lê:

- Trung ương:

+ Vua đứng đầu chính quyền.

+ Phong vương cho các con, trấn giữ nơi quan trọng.

+ Thái sư, đại sư, quan văn, quan võ giúp vua.

- Địa phương: 

+ Lộ, phủ, châu, rồi đến giáp. Đơn vị cơ sở là xã. 

+ Quân đội: cấm quân và quân địa phương.

Nhận xét:

- Bộ máy nhà nước thời Đinh còn chưa hoàn chỉnh, sơ sài. 

- Sang đến thời Tiền Lê, bộ máy nhà nước được hoàn thiện, cải cách hành chính các cấp ở địa phương.

b) Giả sử em là Đinh Tiên Hoàng, em có chọn đặt kinh đô ở Hoa Lư không? Vì sao?

- Phương án 1: Nếu em là Đinh Tiên Hoàng, em sẽ chọn đặt kinh đô ở Hoa Lư. Vì:

+ Hoa Lư là quê hương và là nơi khởi nghiệp của Đinh Tiên Hoàng.

+ Hoa Lư là nơi địa hình hiểm trở, núi non trùng điệp, núi trong sông, sông trong núi. Sau lưng là rừng, trước là đồng bằng, xa nữa là biển... Căn cứ thủy bộ rất thuận tiện, đây là điều kiện thuận lợi để tạo thế phòng thủ đất nước, tránh sự xâm lược từ bên ngoài của kẻ thù vào những buổi đầu độc lập dân tộc.

- Phương án 2: Nếu em là Đinh Tiên Hoàng em sẽ không chọn Hoa Lư làm kinh đô vì:

+ Hoa Lư là nơi có địa hình hiểm trở, xung quanh đều là núi non bao bọc nên nếu bị quân địch bao vây chúng ta sẽ không thể thoát ra ngoài. Như vậy sẽ rất nguy hiểm cho nhân dân và triều đình.

+ Mặt khác, địa thế hiểm trở của Hoa Lư cũng hạn chế sự phát triển của đất nước.

* Lưu ý: Học sinh trình bày quan điểm cá nhân, lập luận chính xác vẫn được điểm. Quan điểm trên chỉ mang tính tham khảo.

a. Địa hình Bắc Mỹ phân hoá thành ba khu vực rõ rệt:

- Miền núi Coóc-đi-e ở phía tây, là một trong những hệ thống núi lớn trên thể giới. Miền núi có độ cao trung bình 3 000 - 4 000m, kéo dài khoảng 9 000km theo chiều bắc - nam, gồm nhiều dãy núi chạy song song, xen giữa là các cao nguyên và sơn nguyên.

- Miền đồng bằng ở giữa bao gồm đồng bằng Ca-na-đa, đồng bằng Lớn, đồng bằng Trung Tâm và đồng bằng Duyên Hải, độ cao từ 200 - 500m, thấp dần từ bắc xuống nam.

- Sơn nguyên trên bán đảo La-bra-đo và dãy núi A-pa-lát ở phía đông, có hướng đông bắc - tây nam. Dãy A-pa-lát gồm 2 phần: phần bắc có độ cao từ 400 - 500m; phần nam cao từ 1 000 - 1 500m.

b. Sự phân hóa tự nhiên theo chiều cao ở Nam Mỹ: 

- Sự phân hoá tự nhiên theo chiều cao ở Nam Mỹ thể hiện rõ nét nhất ở miền núi An-đét:

+ Ở dưới thấp, vùng Bắc và Trung An-đét thuộc các đới khí hậu nóng và ẩm ướt, có rừng mưa nhiệt đới; vùng Nam An-đét thuộc khí hậu ôn hòa, phát triển rừng cận nhiệt và ôn đới.

+ Càng lên cao, thiên nhiên càng thay đổi tương ứng với sự thay đổi của nhiệt độ và độ ẩm.

Giả sử ba số \(a\), \(b\), \(c\) không đồng thời là các số dương thì có ít nhất một số không dương.

Không mất tính tổng quát, ta giả sử \(a \leq 0\).

 Nếu \(a = 0\) thì \(a b c = 0\) (mâu thuẫn với giả thiết \(a b c > 0\));

 Nếu \(a < 0\) thì từ \(a b c > 0 \Rightarrow b c < 0\).

Ta có \(a b + b c + c a > 0 \Leftrightarrow a \left(\right. b + c \left.\right) > - b c \Rightarrow a \left(\right. b + c \left.\right) > 0 \Rightarrow b + c < 0 \Rightarrow a + b + c < 0\) (mâu thuẫn với giả thiết).

Vậy cả ba số \(a\), \(b\) và \(c\) đều dương.