

Trần Thị Khiêm
Giới thiệu về bản thân



































Ta có: \(A = 1 + 4 + 4^{2} + 4^{3} + . . . + 4^{2 \&\text{nbsp}; 024}\)
\(= \left(\right. 1 + 4 + 4^{2} \left.\right) + \left(\right. 4^{3} + 4^{4} + 4^{5} \left.\right) + . . . + \left(\right. 4^{2 \&\text{nbsp}; 022} + 4^{2 \&\text{nbsp}; 023} + 4^{2 \&\text{nbsp}; 024} \left.\right)\)
\(= \left(\right. 1 + 4 + 4^{2} \left.\right) + 4^{3} . \left(\right. 1 + 4 + 4^{2} \left.\right) + . . . + 4^{2 \&\text{nbsp}; 022} \left(\right. 1 + 4 + 4^{2} \left.\right)\)
\(= 21. \left(\right. 1 + 4^{3} + . . . + 4^{2 \&\text{nbsp}; 022} \left.\right)\)
Vì \(21 21\) nên \(A 21\).
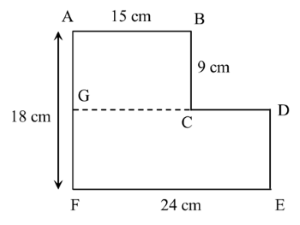

Độ dài CD là \(24 - 15 = 9\) (cm)
Độ dài DE là \(18 - 9 = 9\) (cm)
Chu vi mảnh đất là:
\(15 + 18 + 24 + 9 + 9 + 9 = 84\) (cm)
Diện tích mảnh đất là:
\(15.9 + 9.24 = 351\) (cm\(^{2}\))
Số nhóm được chia phải là ước của cả \(24\) và \(16\).
Số nhóm được chia phải là nhiều nhất có thể.
Vì vậy số nhóm được chia là ƯCLN\(\left(\right. 24 , 16 \left.\right)\).
Ta có ƯCLN\(\left(\right. 24 , 16 \left.\right) = 8\). Vậy chia được nhiều nhất \(8\) nhóm.
Khi đó một nhóm có:
\(24 : 8 = 3\) (nữ)
\(16 : 8 = 2\) (nam)
qdư
Bài 2 (1,5 điểm). Thực hiện phép tính (bằng cách hợp lí nếu có thể).
a) \(36 + 75 + 64 + 25 + 99\);
b) \(2 \&\text{nbsp}; 02 4^{0} + 3. \left[\right. 5^{2} . 10 - \left(\right. 23 - 13 \left.\right)^{2} \left]\right.\);
c) \(4^{2} . 65 + 35. 4^{2} - 1 500\).
Hướng dẫn giải:
a) \(36 + 75 + 64 + 25 + 99\)
\(= \left(\right. 36 + 64 \left.\right) + \left(\right. 75 + 25 \left.\right) + 99\)
\(= 100 + 100 + 99\)
\(= 200 + 99\)
\(= 299.\)
b) \(2 02 4^{0} + 3. \left[\right. 5^{2} . 10 - \left(\right. 23 - 13 \left.\right)^{2} \left]\right.\)
\(= 1 + 3. \left(\right. 25.10 - 1 0^{2} \left.\right)\)
\(= 1 + 3. \left(\right. 250 - 100 \left.\right)\)
\(= 1 + 3.150 = 451.\)
c) \(4^{2} . 65 + 35. 4^{2} - 1 500\)
\(= 16.65 + 35.16 - 1 500\)
\(= 16 \left(\right. 65 + 35 \left.\right) - 1 500\)
\(= 16.100 - 1 500\)
\(= 1 600 - 1 500\)
\(= 100\).
a) :M = {Cam tươi; Cóc ổi; Dưa hấu}.
b) Điền kí hiệu \(\in\) và \(\notin\) thích hợp vào ô trống.
Đào \(\notin\) \(M\); Cóc \(\notin\) \(M\); Dưa hấu \(\in\) \(M\).
c)
\(2\) cốc Cam tươi và \(3\) cốc Dưa hấu có giá là:
\(23 000.2 + 25 000.3 = 121 000\) (đồng)
Vậy mẹ của Hạnh đủ tiền để mua (vì \(121 000 < 150 000\)).
Bài 1:
a)
- Thanh \(A B\) không đáng kể khối lượng, treo tại điểm \(O\) (cách A một đoạn \(O A = \frac{1}{4} A B\)).
- Tại \(A\) treo vật \(m_{1} = 2 \textrm{ } k g\).
- Tại \(B\) treo vật \(m_{2}\).
- Yêu cầu: Tìm \(m_{2}\) để thanh cân bằng.
Giải:
Điều kiện cân bằng momen tại điểm \(O\):
\(m_{1} g \cdot O A = m_{2} g \cdot O B .\)Trong đó:
- \(O A = \frac{1}{4} A B\).
- \(O B = A B - O A = \frac{3}{4} A B\).
Suy ra:
\(m_{1} \cdot \frac{1}{4} A B = m_{2} \cdot \frac{3}{4} A B .\) \(m_{2} = \frac{m_{1}}{3} = \frac{2}{3} \textrm{ } k g .\)✅ Kết quả: \(m_{2} = \frac{2}{3} \textrm{ } k g\).
b)
- Vật \(m_{1}\) được nhúng vào chất lỏng có khối lượng riêng bằng ½ khối lượng riêng của vật.
- Khi đó lực đẩy Ác-si-mét:
→ \(F_{A} = \frac{1}{2} m_{1} g\).
Vậy trọng lượng biểu kiến của \(m_{1}\):
\(P^{'} = m_{1} g - F_{A} = m_{1} g - \frac{1}{2} m_{1} g = \frac{1}{2} m_{1} g .\)Thay \(m_{1} = 2 \textrm{ } k g\):
\(P^{'} = \left(\right. 1 \textrm{ } k g \left.\right) \cdot g .\)Nghĩa là khối lượng hiệu dụng còn 1 kg.
Khi cân bằng:
\(m_{1}^{'} \cdot O A = m_{2} \cdot x ,\)trong đó \(m_{1}^{'} = 1 \textrm{ } k g\), \(O A = \frac{1}{4} A B\), và \(x\) là khoảng cách từ \(O\) đến vị trí treo \(m_{2}\).
\(1 \cdot \frac{1}{4} A B = \frac{2}{3} \cdot x .\) \(x = \frac{\frac{1}{4} A B}{\frac{2}{3}} = \frac{3}{8} A B .\)✅ Vậy: Muốn cân bằng, phải treo \(m_{2}\) tại điểm cách \(O\) một đoạn \(\frac{3}{8} A B\) về phía \(B\).
Bài 2:
Một thanh kim loại quay quanh điểm \(O\).
- Điểm \(A\) cách điểm treo \(D\) một đoạn 0,6 m.
- Tại \(A\) treo \(m_{1} = 7 , 5 \textrm{ } k g\).
- Tại đầu \(D\) nối ròng rọc động treo vật \(m_{2} = 10 \textrm{ } k g\).
- Yêu cầu: tính chiều dài thanh.
👉 Đoạn này hơi dài, bạn có muốn mình trình bày chi tiết bước giải cho bài 2 luôn không (gồm phân tích lực căng dây, ròng rọc động giảm lực còn \(m_{2} g / 2\), lập phương trình cân bằng momen quanh \(O\))?
Bài 1:
a)
- Thanh \(A B\) không đáng kể khối lượng, treo tại điểm \(O\) (cách A một đoạn \(O A = \frac{1}{4} A B\)).
- Tại \(A\) treo vật \(m_{1} = 2 \textrm{ } k g\).
- Tại \(B\) treo vật \(m_{2}\).
- Yêu cầu: Tìm \(m_{2}\) để thanh cân bằng.
Giải:
Điều kiện cân bằng momen tại điểm \(O\):
\(m_{1} g \cdot O A = m_{2} g \cdot O B .\)Trong đó:
- \(O A = \frac{1}{4} A B\).
- \(O B = A B - O A = \frac{3}{4} A B\).
Suy ra:
\(m_{1} \cdot \frac{1}{4} A B = m_{2} \cdot \frac{3}{4} A B .\) \(m_{2} = \frac{m_{1}}{3} = \frac{2}{3} \textrm{ } k g .\)✅ Kết quả: \(m_{2} = \frac{2}{3} \textrm{ } k g\).
b)
- Vật \(m_{1}\) được nhúng vào chất lỏng có khối lượng riêng bằng ½ khối lượng riêng của vật.
- Khi đó lực đẩy Ác-si-mét:
→ \(F_{A} = \frac{1}{2} m_{1} g\).
Vậy trọng lượng biểu kiến của \(m_{1}\):
\(P^{'} = m_{1} g - F_{A} = m_{1} g - \frac{1}{2} m_{1} g = \frac{1}{2} m_{1} g .\)Thay \(m_{1} = 2 \textrm{ } k g\):
\(P^{'} = \left(\right. 1 \textrm{ } k g \left.\right) \cdot g .\)Nghĩa là khối lượng hiệu dụng còn 1 kg.
Khi cân bằng:
\(m_{1}^{'} \cdot O A = m_{2} \cdot x ,\)trong đó \(m_{1}^{'} = 1 \textrm{ } k g\), \(O A = \frac{1}{4} A B\), và \(x\) là khoảng cách từ \(O\) đến vị trí treo \(m_{2}\).
\(1 \cdot \frac{1}{4} A B = \frac{2}{3} \cdot x .\) \(x = \frac{\frac{1}{4} A B}{\frac{2}{3}} = \frac{3}{8} A B .\)✅ Vậy: Muốn cân bằng, phải treo \(m_{2}\) tại điểm cách \(O\) một đoạn \(\frac{3}{8} A B\) về phía \(B\).
Bài 2:
Một thanh kim loại quay quanh điểm \(O\).
- Điểm \(A\) cách điểm treo \(D\) một đoạn 0,6 m.
- Tại \(A\) treo \(m_{1} = 7 , 5 \textrm{ } k g\).
- Tại đầu \(D\) nối ròng rọc động treo vật \(m_{2} = 10 \textrm{ } k g\).
- Yêu cầu: tính chiều dài thanh.
Đề:
- Người A và B có số táo bằng nhau, gọi là \(n\) quả mỗi người.
- Giá dự kiến:
- A bán \(10000 / 3\) quả (≈ 3333 đ/quả).
- B bán \(10000 / 2\) quả (5000 đ/quả).
- Thực tế: B gộp chung, bán \(20000 / 5\) quả (4000 đ/quả).
- Sau khi bán hết, đếm tiền thì thiếu 15000 đ so với dự kiến.
- Hỏi số tiền của B thực thu nhiều hơn A bao nhiêu?
Bước 1: Tính tiền dự kiến nếu bán riêng
- A dự kiến:
\(T_{A} = \frac{10000}{3} \cdot n = \frac{10000 n}{3} .\) - B dự kiến:
\(T_{B} = \frac{10000}{2} \cdot n = 5000 n .\) - Tổng dự kiến:
\(T = \frac{10000 n}{3} + 5000 n .\)
Bước 2: Tính tiền thực tế khi gộp bán
- Tổng số táo: \(2 n\).
- Giá bán: \(20000 / 5 = 4000\) đ/quả.
- Tổng tiền thu được:
\(T^{'} = 4000 \cdot 2 n = 8000 n .\)
Bước 3: Lập phương trình “thiếu 15000 đ”
\(T - T^{'} = 15000.\)
Thay vào:
\(\left(\right. \frac{10000 n}{3} + 5000 n \left.\right) - 8000 n = 15000.\) \(\frac{10000 n}{3} - 3000 n = 15000.\) \(\frac{10000 n - 9000 n}{3} = 15000.\) \(\frac{1000 n}{3} = 15000 \Rightarrow n = 45.\)
Bước 4: Tính tiền của A và B trong thực tế
- A có 45 quả. Bán chung giá 4000 đ/quả →
\(T_{A}^{'} = 45 \cdot 4000 = 180000\). - B cũng 45 quả →
\(T_{B}^{'} = 45 \cdot 4000 = 180000\).
Bước 5: So sánh
- Dự kiến:
- A: \(\frac{10000}{3} \cdot 45 = 150000\).
- B: \(5000 \cdot 45 = 225000\).
- Thực tế:
- A: 180000.
- B: 180000.
→ Người A lãi thêm \(30000\) so với dự kiến.
→ Người B mất đi \(45000\) so với dự kiến.
→ So sánh A và B trong thực tế:
\(180000 - 180000 = 0.\)
✅ Kết quả:
Trong thực tế, số tiền của B không nhiều hơn A → hai người thu bằng nhau.
Nhưng vì đề hỏi “B thu ít hơn so với dự kiến bao nhiêu?” thì ta có: người B thu ít hơn người A 0 đồng, nhưng so với dự kiến thì B mất 45.000 đồng còn A được lợi 30.000 đồng.