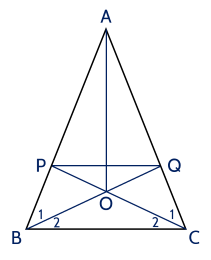
a)△ABC cân tại A nên ABC=ACB.

Vì BQ và CP là đường phân giác của B,C nên 2B1​​=B2​​=2ABC​, 2C1​​=C2​​=2ACB​.

Do đó B1​​=B2​​=C1​​=C2​​.

Suy ra △OBC cân tại O.

b) Vì O là giao điểm các đường phân giác CP và BQ trong △ABC nên O là giao điểm ba đường phân giác trong △ABC.

Do đó, O cách đều ba cạnh AB,AC và BC.

c) Ta có △ABC cân tại A,AO là đường phân giác của góc A nên AO đồng thời là trung tuyến và đường cao của △ABC.

Vậy đường thẳng AO đi qua trung điểm của đoạn thẳng BC và vuông góc với nó.

d) Ta có △PBC=△QCB (g.c.g)

⇒CP=BQ (hai cạnh tương ứng).

e) Ta có AP=AB−BP, AQ=AC−CQ (1);

△PBC=△QCB⇒BP=CQ (2).

Lại có AB=AC (tam giác ABC cân tại A) (3).

Từ (1), (2) và (3) suy ra AP=AQ.

Vậy tam giác APQ cân tại A.

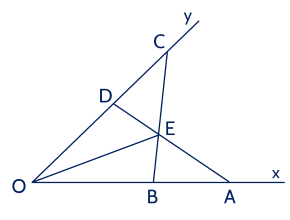
a) Xét △OAD và △OCB, có

OA=OC (giả thiết);

^O chung;

OD=OB (giả thiết).

Do đó △OAD=△OCB (c.g.c)

AD=CB (hai cạnh tương ứng).

b) Do OA=OC và OB=OD nên AB=CD.

Mà △OAD=△OCB (chứng minh trên)

⇒OBC=ODA; OAD=OCB (hai góc tương ứng)

Mặt khác ABE+OBC=CDE+ODA=180∘

⇒ABE=CDE

Xét △ABE và △CDE có

OAD=OCB (chứng minh trên);

AB=CD (chứng minh trên);

ABE=CDE (chứng minh trên) 

Do đó △ABE=△CDE (g.c.g).

c) Vi △ABE=△CDE (chứng minh trên) nên AE=CE (hai cạnh tương ứng).

Xét △AEO và △CEO có AE=CE (chứng minh trên);

OE cạnh chung;

OA=OC (giả thiết).

Do đó △AEO=△CEO (c.c.c)

⇒AOE=COE (hai góc tương ứng)

⇒OE là tia phân giác của xOy​.

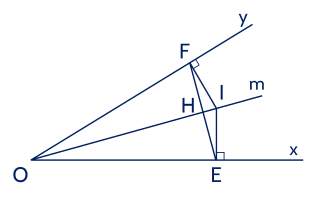
a) Xét △IOE và △IOF có

E=F=90∘ (giả thiết);

OI cạnh chung;

EOI=FOI (Om là tia phân giác).

Vậy △IOE=△IOF (cạnh huyền - góc nhọn).

b) △IOE=△IOF (chứng minh trên)

⇒OE=OF (hai cạnh tương ứng).

Gọi H là giao điểm của Om và EF.

Xét △OHE và △OHF, có

OE=OF (chứng minh trên);

EOH=FOH (Om là tia phân giác);

OHOH chung.

Do đó △OHE=△OHF (c.g.c)

⇒OHE=FHO (hai góc tương ứng)

Mà OHE+FHO=180∘ nên OHE=FHO=90∘.

Vậy EF⊥Om.

KẻIE⊥AD (với E∈AD).

Gọi Ax là tia đối của tia AB.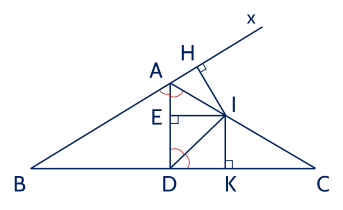

Vì ^BAC và ^CAx là hai góc kề bù
mà BAC=120∘ nên CAx=60∘ (1) 

Ta có AD là phân giác của BAC⇒DAC=1/2​BAC=60∘ (2)

Từ (1) và (2) suy ra AC là tia phân giác của ^DAx

⇒IH=IE (tính chất tia phân giác của một góc) (3)

Vì DI là phân giác của ^ADC nên IK=IE (tính chất tia phân giác của một góc) (4)

Từ (3) và (4)(4) suy ra IH=IK.

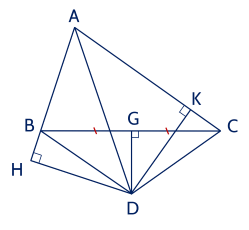
Ta có D thuộc phân giác của ^A;

DH⊥AB; DK⊥AC ⇒DH=DK (tính chất tia phân giác của một góc).

Gọi G là trung điểm củaBC.

Xét △BGD và △CGD, có

BGD=CGD=90∘ (DG là trung trực của BC ),

BG=CG (già thiết),

DG là cạnh chung.

Do đó △BGD=△CGD (hai cạnh góc vuông)

⇒BD=CD (hai cạnh tương ứng).

Xét △BHD và △CKD, có

BHD=CKD=90∘ (giả thiết);

DH=DK (chứng minh trên);

BD=CD (chứng minh trên).

Do đó △BHD=△CKD (cạnh huyền - cạnh góc vuông)

⇒BH=CK (hai cạnh tương ứng).

Câu 2:
a, B(x) = 7x^2 - x^4 - x - 7x^3 - 2x^2 + 11x^3 - x^4
B(x) = (7x^2 - 2x^2) - (x^4 - x^4) - x - (7x^3 + 11x^3)
B(x) = 5x^2 - 0 - x - 18x^3
B(x) = 5x^2 - x - 18x^3
Đa thức B(x) được sắp xếp theo số mũ tăng dần của biến là:
B(x) = 18x^3 - 5x^2 - x
b, Bậc của đa thức B(x) là 3
Hệ số cao nhất của đa thức B(x) là 18
Hệ số tự do của đa thức B(x) là 0
c, Ta có: B(x) = 7x^2 - x^4 - x - 7x^3 - 2x^2 + 11x^3 - x^4
Khi x=-1, có:
B(-1) = 7.(-1)^2 - (-1)^4 - (-1) - 7.(-1)^3 - 2.(-1)^2 + 11.(-1)^3 - (-1)^4
B(-1) = 7.1-1+1-[7.(-1)]-2.1+[11.(-1)]-1
B(-1) = 7-1+1+7-2-11-1 (mình có đổi dấu rồi nhé)
B(-1) = 0
d, Ta có: B(x) = 7x^2 - x^4 - x - 7x^3 - 2x^2 + 11x^3 - x^4
Khi x=0, có:
B(0) = 7.0^2 - 0^4 - 0 - 7.0^3 - 2.0^2 + 11.0^3 - 0^4
B(0) = 7.0 - 0 - 0 - (7.0) - (2.0) + (11.0) - 0
B(0) = 0-0-0-0-0+0-0
B(0) = 0
Vậy x=0 có là nghiệm của đa thức B(x)
Mình tự làm có gì sai sót thì bỏ qua nhé
(Cho mình 1 tick nhaa)

Câu 1:
a, A(x) = 5x^3 + x^4 - 1/2x - 7x^3 - 2x^2 + 6 - x^4
A(x) = (5x^3 - 7x^3) + (x^4 - x^4) - 1/2x -2x^2 +6
A(x) = -2x^3 + 0 - 1/2x - 2x^2 +6
A(x) = -2x^3 - 1/2x - 2x^2 +6
Đa thức A(x) được sắp xếp theo luỹ thừa giảm dần của biến là:
A(x) = -2x^3 - 2x^2 - 1/2x + 6
b, Bậc của đa thức A(x) là: 3
Các hệ số của đa thức A(x) là: -2, 1/2, 2, 6
c, Ta có: A(x) = 5x^3 + x^4 - 1/2x - 7x^3 - 2x^2 + 6 - x^4
Khi x=1, có:
A(1) = 5.1^3 + 1^4 - (1/2.1) - (7.1^3) - (2.1^2) + 6 - 1^4
A(1) = 5.1 + 1 - 1/2 - (7.1) -(2.1) + 6 - 1
A(1) = 5 + 1 - 1/2 - 7 - 2 + 6 - 1
A(1) = 3/2
d, Ta có: A(x) = 5x^3 + x^4 - 1/2x - 7x^3 - 2x^2 + 6 - x^4
Khi x=0, có:
A(0) = 5.0^3 + 0^4 - 1/2.0 - 7.0^3 - 2.0^2 + 6 - 0^4
A(0) = 5.0+0-0-(7.0)-(2.0)+6-0
A(0) = 0+0-0-0-0+6-0
A(0) = 6
Vậy x=0 không phải là nghiệm của đa thức A(x)
mình làm tạm bài 1 trc nhé bn chép đi để mình soạn nốt câu 2

cay

bạn chép phần mở bài và thân bài từ dàn ý rồi phần liên hệ, đánh giá với kết bài bạn tự bịa ra hoặc hỏi ChatGPT là đc mà

là tạm biệt:))