

Nguyễn Thị Thảo Quyên
Giới thiệu về bản thân



































a. Đặc điểm khí hậu của Ô-xtrây-li-a.
- Dải bờ biển hẹp phía Bắc lục địa:
+ Tính chất: cận xích đạo.
+ Nóng, ẩm.
+ Mưa nhiều, lượng mưa từ 1.000 - 1.5000 mm/năm.
- Khí hậu nhiệt đới chiếm phần lớn lục địa nhưng khác biệt từ Tây sang Đông.
+ Sườn Đông dãy Trường Sơn Ô-xtrây-li-a có khí hậu nhiệt đới: Ẩm, mưa nhiều, thời tiết mát mẻ và lượng mưa từ 1.000 - 1.500 mm/năm.
+ Từ sườn Tây dãy Trường Sơn Ô-xtrây-li-a đến bờ Tây lục địa có khí hậu nhiệt đới lục địa khắc nghiệt: Độ ẩm rất thấp, ít mưa (ở trung tâm, lượng mưa dưới 250 mm/năm). Mùa hạ nóng, mùa đông tương đối lạnh.
- Dải đất hẹp phía Nam lục địa: khí hậu cận nhiệt đới: Mùa hạ nóng, mùa đông ấm áp, lượng mưa dưới 1.000 mm/năm.
- Phía Nam đảo Ta-xma-ni-a: khí hậu ôn đới.
b. Nguyên nhân dẫn đến sự độc đáo về dân cư, xã hội của Ô-xtrây-li-a:
- Sự du nhập của dân cư từ khắp các châu lục trên thế giới.
- Lịch sử phát triển lãnh thổ khá lâu đời.
Hướng dẫn giải:
Số đã cho: 1 053 194.
a) Chữ số hàng chục nghìn của số trên là chữ số 5, có giá trị là 50 000.
b) Do chữ số hàng chục nghìn của số trên là 5 nên khi làm tròn số đó đến hàng trăm nghìn, ta được số 1 100 000 (làm tròn lên).
Hướng dẫn giải:
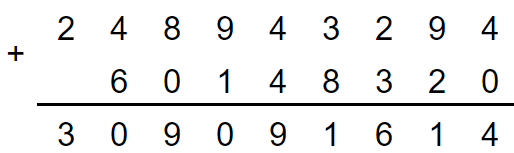
a) 248 943 294 + 60 148 320
b) 34 506 728 − 8 243 809

c) 23 729 × 2
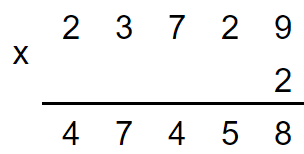
d) 17 423 : 3
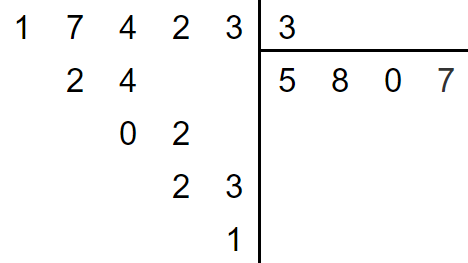
mình đã tặng cô 350 xu vì cô thích xu nên cho cô
Ta cùng giải bài toán này nhé 👇
Bài toán:
- Hai bạn Bình và Định chạy ngược chiều nhau trên một đường tròn.
- Vận tốc Bình: \(v_{1} = 4 , 5 \textrm{ } \text{m}/\text{s}\)
- Vận tốc Định: \(v_{2} = 5 , 5 \textrm{ } \text{m}/\text{s}\)
- Thời gian gặp nhau lần đầu: \(t = 40 \textrm{ } \text{s}\)
Bước 1: Xác định vận tốc tương đối
Khi chạy ngược chiều nhau, quãng đường mà cả hai cùng đi được cho đến lúc gặp nhau chính bằng chu vi đường chạy.
Vận tốc tương đối:
\(v = v_{1} + v_{2} = 4 , 5 + 5 , 5 = 10 \textrm{ } \text{m}/\text{s}\)
Bước 2: Tính quãng đường gặp nhau
Trong thời gian \(t = 40\) giây, tổng quãng đường cả hai đi được:
\(S = v \times t = 10 \times 40 = 400 \textrm{ } \text{m}\)
Kết quả:
Độ dài đường chạy (chu vi sân) là:
400m
Công thức tính diện tích hình chữ nhật là:
\(S = a \times b\)
Trong đó:
- \(a\) là chiều dài,
- \(b\) là chiều rộng,
- \(S\) là diện tích hình chữ nhật. ✅
- Ok, mình làm ví dụ cụ thể nhé 🙂
Ví dụ:
Một hình chữ nhật có chiều dài \(a = 12 \textrm{ } c m\) và chiều rộng \(b = 5 \textrm{ } c m\).
Tính diện tích hình chữ nhật đó.
Bài giải:
\(S = a \times b = 12 \times 5 = 60 \textrm{ } \left(\right. c m^{2} \left.\right)\)
👉 Vậy diện tích hình chữ nhật là 60 cm²
Ta cùng tính từng bước:
\(2 + \left(\right. 8 \times 8 \times 2 \left.\right) \times 56\)- \(8 \times 8 = 64\)
- \(64 \times 2 = 128\)
- \(128 \times 56 = 7168\)
- \(2 + 7168 = 7170\)
👉 Kết quả là 7170 ✅
Question 1: last night - dấu hiệu thì quá khứ đơn
(-) S + didn’t + V(bare-inf).
thirsty là tính từ → cần to be ở trước. Chủ ngữ “I” → to be: was
Đáp án: Last night, I didn't order a milkshake because I was not thirsty.
Dịch: Tối qua tôi không gọi sữa lắc vì tôi không khát.
Question 2: time - N(không đếm được) → dùng How much
spend time/money on something
each day - dấu hiệu thì hiện tại đơn
Đáp án: How much time do you spend on math homework each day?
Dịch: Bạn dành bao nhiêu thời gian cho bài tập toán mỗi ngày?
Question 3: to be + the + tính từ ngắn - est
heavy tận cùng là y → coi là tính từ ngắn
Đáp án: Eating fruits and vegetables is the healthiest way to stay fit.
Dịch: Ăn trái cây và rau quả là cách lành mạnh nhất để giữ dáng.
Question 1: to be interested in V-ing = fancy V-ing: thích làm gì
Đáp án: I fancy taking part in a clean-up event this month.
Dịch: Tôi thích tham gia vào một sự kiện dọn dẹp trong tháng này.
Question 2: to be as + tính từ + as = to be the same + danh từ + as
Đáp án: The bookshelves are the same height as the windows.
Dịch: Giá sách có cùng chiều cao với cửa sổ.
Question 3: Mẫu câu đề nghị
Let’s V. = Why don’t we V?
Đáp án: Why don’t we collect old plastic bottles and paper in our school?
Dịch: Sao chúng ta không thu thập chai nhựa và giấy đã sử dụng ở trường?
Question 4: Dùng “and” để nối các phần có cùng chức năng
Đáp án: My friends and I go to the studio to practice dancing.
Dịch: Tôi và bạn bè tới studio để tập nhảy.
Question 1: We planted trees together in the community garden a month ago.
Question 2: Her voice is as beautiful as a melody from a fairy tale.
Question 3: We have a school assembly in the school yard on Monday mornings.