
mn cho mình xin cách giải 2 bài này với ạ!:>
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: 4/25=16/100
-7/4=-175/100
9/50=18/100
b: -7/10=-28/40
11/20=22/40
-10/40=-10/40
c: 5/18=10/36
7/12=21/36
11/6=66/36

31−43−(−53)+721−92−361+151
=\frac{1}{3}-\frac{3}{4}+\frac{3}{5}+\frac{1}{72}-\frac{2}{9}-\frac{1}{36}+\frac{1}{15}=31−43+53+721−92−361+151
=\left(\frac{1}{3}-\frac{2}{9}\right)+\left(-\frac{3}{4}-\frac{1}{36}\right)+\left(\frac{3}{5}+\frac{1}{15}\right)+\frac{1}{72}=(31−92)+(−43−361)+(53+151)+721
=\left(\frac{3}{9}-\frac{2}{9}\right)+\left(-\frac{27}{36}-\frac{1}{36}\right)+\left(\frac{9}{15}+\frac{1}{15}\right)+\frac{1}{72}=(93−92)+(−3627−361)+(159+151)+721
=\frac{1}{9}+\frac{-7}{9}+\frac{2}{3}+\frac{1}{72}=91+9−7+32+721
=-\frac{2}{3}+\frac{2}{3}+\frac{1}{72}=−32+32+721
=0+\frac{1}{72}=\frac{1}{72}=0+721=721

#include <bits/stdc++.h>
using namespace std;
int main (){
int n;
cin >> n;
int a[n];
long long t=0,k=0;
for (int i=1;i<=n;i++) cin >> a[i];
for (int i=1;i<=n;i++) {
int lt=1;
for (int j=1;j<=i;j++)
lt=lt*a[i];
t=t+lt;
}
cout << t;
return 0;
}

\(y'=-3mx^2+2x-3\)
Hàm nghịch biến trên khoảng đã cho khi với mọi \(x\in\left(-3;0\right)\) ta có:
\(-3mx^2+2x-3\le0\)
\(\Leftrightarrow2x-3\le3mx^2\)
\(\Leftrightarrow\dfrac{2x-3}{3x^2}\le m\)
\(\Rightarrow m\ge\max\limits_{\left(-3;0\right)}\left(\dfrac{2x-3}{3x^2}\right)\)
Xét hàm \(f\left(x\right)=\dfrac{2x-3}{3x^2}\Rightarrow f'\left(x\right)=\dfrac{2\left(3-x\right)}{3x^3}< 0;\forall x\in\left(-3;0\right)\)
\(\Rightarrow f\left(x\right)>f\left(-3\right)=-\dfrac{1}{3}\)
\(\Rightarrow m\ge-\dfrac{1}{3}\)

10:
\(a+b=50^0+40^0=90^0\)
=>\(sina=cosb;sinb=cosa;tana=cotb;cota=tanb\)
=>sina=cosb
=>Chọn C
11:
Xét ΔABC vuông tại A có \(AC=BC\cdot sinB\)
=>\(AC=12\cdot sin30=6\)
=>Chọn B

A = 4 + 4² + 4³ + ... + 4¹⁰⁰
⇒ 4A = 4² + 4³ + 4⁴ + ... + 4¹⁰¹
⇒ 3A = 4A - A
= (4² + 4³ + 4⁴ + ... + 4¹⁰¹) - (4 + 4² + 4³ + ... + 4¹⁰⁰)
= 4¹⁰¹ - 4
⇒ 12A = 4.3A = 4.(4¹⁰¹ - 4)
= 4¹⁰² - 4²
⇒ 12A + 4² = 4¹⁰²
Mà 12A + 4² = 4ⁿ
⇒ 4ⁿ = 4¹⁰²
⇒ n = 102
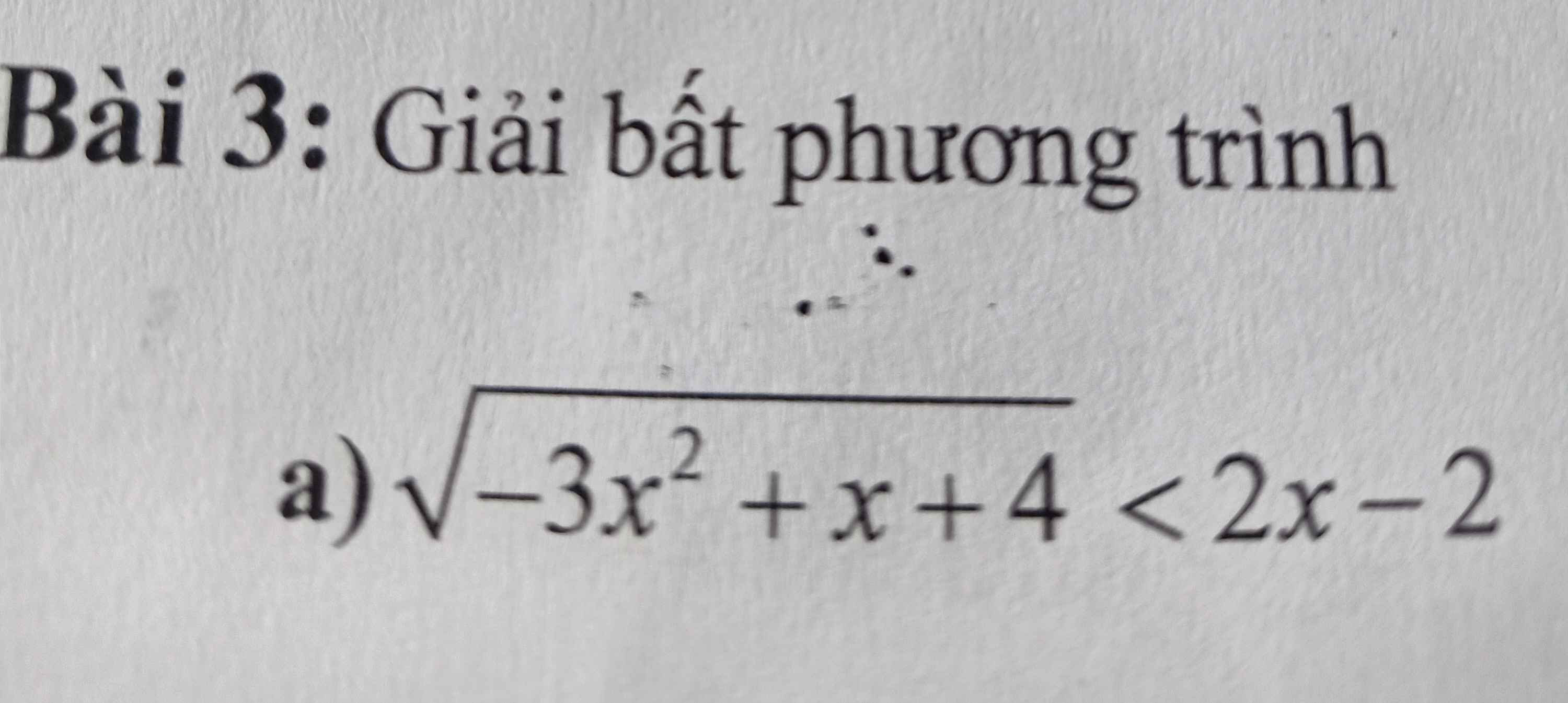
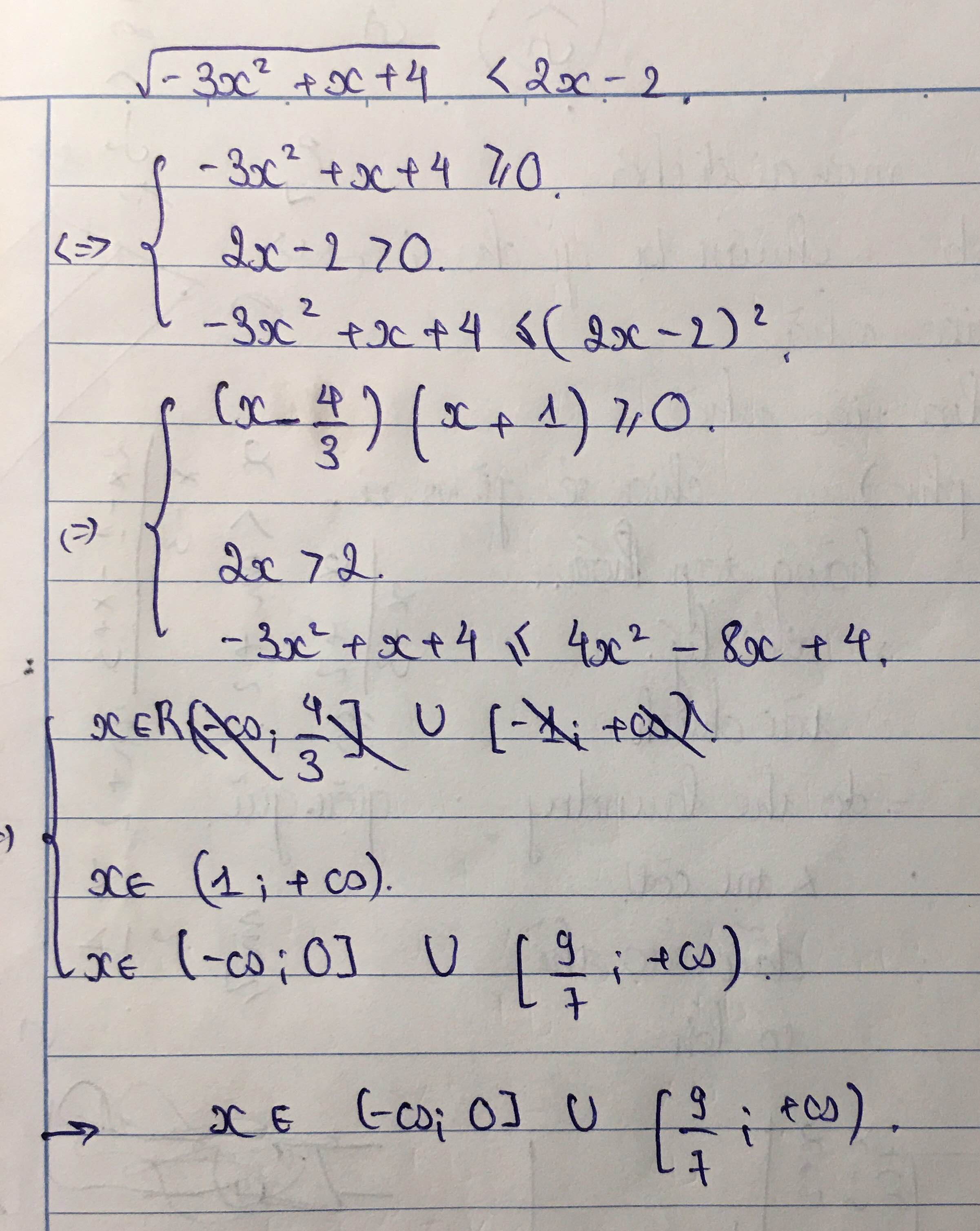
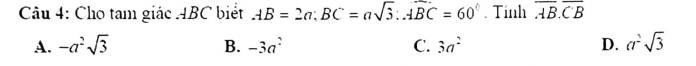
 cho em xin cách giải và đáp án bài này với ạ
cho em xin cách giải và đáp án bài này với ạ

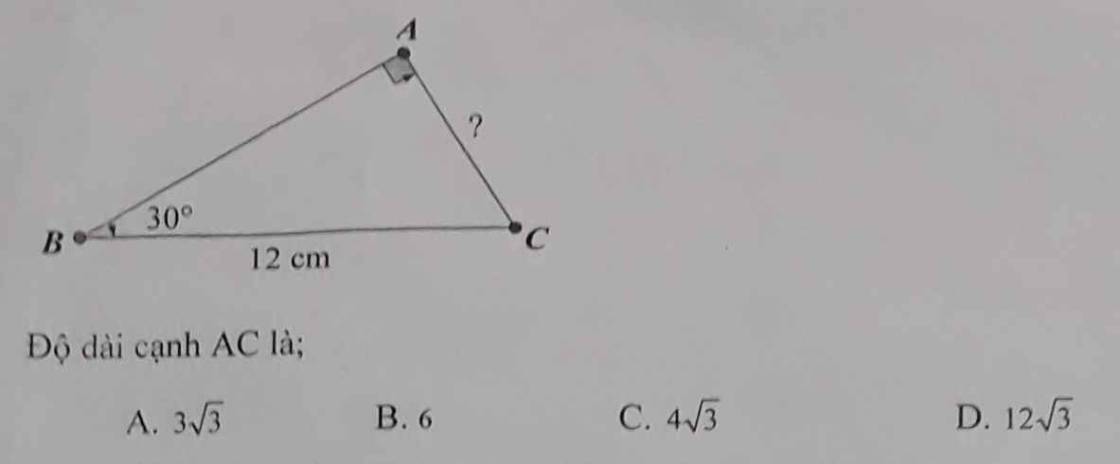
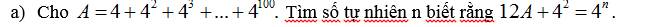 cho mình xin lời giải và công thức bài này với ạ !!!
cho mình xin lời giải và công thức bài này với ạ !!!