(x+1)^3-(x^3+3x)=-5
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
10 tháng 11 2021
\(A=2x^3+3x^2-3-5x^2-5x=2x^3-2x^2-5x-3\\ B=125-150x+60x^2-8x^3-25+9x^2=-8x^3+69x^2-150x+100\\ C=\left(3x+1-2x+1\right)\left(3x+1+2x-1\right)=5x\left(x+2\right)=5x^2+10x\\ D=\left(2x+1-3+x\right)^2=\left(3x-2\right)^2=9x^2-12x+4\\ E=x^3-6x^2+12x-8-x^3+x+6x^2-18x=-5x-8\\ F=x^3-3x^2+3x-1-3+3x^2-x^3+1-3x=-3\)
16 tháng 6 2023
1: \(=6x^2+2x-15x-5-x^2+6x-9+4x^2+20x+25-27x^3-27x^2-9x-1\)
=-27x^3-18x^2+4x+10
2: =4x^2-1-6x^2-9x+4x+6-x^3+3x^2-3x+1+8x^3+36x^2+54x+27
=7x^3+37x^2+46x+33
5:
\(=25x^2-1-x^3-27-4x^2-16x-16-9x^2+24x-16+\left(2x-5\right)^3\)
\(=8x^3-60x^2+150-125+12x^2-x^3+8x-60\)
=7x^3-48x^2+8x-35
PT
18 tháng 9 2018
a) \(3\left(x^2-2x+1\right)+x\left(2-3x\right)=7\)
\(\Rightarrow3x^2-6x+3+2x-3x^2=7\)
\(\Rightarrow-4x+3=7\)
\(\Rightarrow-4x+3-7=0\)
\(\Rightarrow-4x-4=0\)
\(\Rightarrow-4\left(x+1\right)=0\)
\(\Rightarrow x+1=0\)
\(\Rightarrow x=-1\)
b) \(5\left(x-2\right)+2\left(x+3\right)=10\)
\(\Rightarrow5x-10+2x+6=10\)
\(\Rightarrow7x-4=10\)
\(\Rightarrow7x=10+4=14\)
\(\Rightarrow x=\dfrac{14}{7}=2\)
c) \(\left(x+1\right)\left(-3\right)+5\left(x-4\right)=-3\)
\(\Rightarrow-3x-3+5x-20=-3\)
\(\Rightarrow2x-23=-3\)
\(\Rightarrow2x=-3+23=20\)
\(\Rightarrow x=\dfrac{20}{2}=10\)
d) \(2\left(x-1\right)-x\left(3-x\right)=x^2\)
\(\Rightarrow2x-2-3x+x^2=x^2\)
\(\Rightarrow-x-2+x^2-x^2=0\)
\(\Rightarrow-x-2=0\)
\(\Rightarrow-x=2\)
\(\Rightarrow x=-2\)
đ) \(3x\left(x+5\right)-2\left(x+5\right)=3x^2\)
\(\Rightarrow3x^2+15x-2x-10=3x^2\)
\(\Rightarrow3x^2-3x^2+13x-10=0\)
\(\Rightarrow13x-10=0\)
\(\Rightarrow13x=10\)
\(\Rightarrow x=\dfrac{10}{13}\)
e) \(4x\left(x+2\right)+x\left(4-x\right)=3x^2+12\)
\(\Rightarrow4x^2+8x+4x-x^2=3x^2+12\)
\(\Rightarrow3x^2+12x=3x^2+12\)
\(\Rightarrow3x^2+12x-3x^2-12=0\)
\(\Rightarrow12\left(x-1\right)=0\)
\(\Rightarrow x-1=0\)
\(\Rightarrow x=1\)
f) \(\dfrac{1}{3}x\left(3x+6\right)-x\left(x-5\right)=9\)
\(\Rightarrow x^2+2x-x^2+5x=9\)
\(\Rightarrow7x=9\)
\(\Rightarrow x=\dfrac{9}{7}\)
8 tháng 9 2023
2:
a: =>x^2+3x-4x-12-(x^2-5x+x-5)=8
=>x^2-x-12-x^2+4x+5=8
=>3x-7=8
=>3x=15
=>x=5
b: =>3x^2+3x-2x-2-3x^2-21x=13
=>-20x=15
=>x=-3/4
c: =>x^2-25-x^2-2x=9
=>-2x=25+9=34
=>x=-17
d: =>x^3-1-x^3+3x=1
=>3x-1=1
=>3x=2
=>x=2/3
8 tháng 6 2019
Tìm x:
1. 3x (2x + 3) - (2x + 5).(3x - 2) = 8
\(\Leftrightarrow6x^2+9x-6x^2+4x-15x+10=0 \)
\(\Leftrightarrow-2x+10=0\Leftrightarrow x=5\)
Vậy x = 5
2. 4x (x -1) - 3(x2 - 5) -x2 = (x - 3) - (x + 4)
\(\Leftrightarrow4x^2-4x-3x^2+15-x^2=x-3-x-4\)
\(\Leftrightarrow-4x+15=-7\)
\(\Leftrightarrow-4x=-22\Leftrightarrow x=\frac{11}{2}\)
Vậy x = \(\frac{11}{2}\)
3. 2 (3x -1) (2x +5) - 6 (2x - 1) (x + 2) = -6
\(\Leftrightarrow2\left(6x^2+15x-2x-5\right)-6\left(2x^2+4x-x-2\right)=-6\)
\(\Leftrightarrow12x^2+30x-4x-10-12x^2-24x+6x+12=-6\)
\(\Leftrightarrow8x=-8\Leftrightarrow x=-1\)
Vậy x = -1
4. 3 ( 2x - 1) (3x - 1) - (2x - 3) (9x - 1) - 3 = -3
\(\Leftrightarrow3\left(6x^2-2x-3x+1\right)-18x^2+2x+27x-3-3=-3\)
\(\Leftrightarrow18x^2-6x-9x+3-18x^2+2x+27x-6=-3\)
\(\Leftrightarrow14x=0\Leftrightarrow x=0\)
Vậy x = 0
5. (3x - 1) (2x + 7) - ( x + 1) (6x - 5) = (x + 2) - (x - 5)
\(\Leftrightarrow6x^2+21x-2x-7-6x^2+5x-6x+5=7\)
\(\Leftrightarrow18x=9\Leftrightarrow x=\frac{1}{2}\)
Vậy x = \(\frac{1}{2}\)
6. 3xy (x + y) - (x + y) (x2 + y2 + 2xy) + y3 = 27
\(\Leftrightarrow3x^2y+3xy^2-\left(x+y\right)^3+y^3=27\)
\(\Leftrightarrow3x^2y+3xy^2-x^3-y^3-3x^2y-3xy^2+y^3=27\)
\(\Leftrightarrow-x^3=27\)
\(\Leftrightarrow x=-3\)
Vậy x = -3
7. 3x (8x - 4) - 6x (4x - 3) = 30
\(\Leftrightarrow24x^2-12x-24x^2+12x=30\)
\(\Leftrightarrow0=30\) ( vô lý)
Vậy pt vô nghiệm
8. 3x (5 - 2x) + 2x (3x - 5) = 20
\(\Leftrightarrow15x-6x^2+6x^2-10x=20\)
\(\Leftrightarrow5x=20\Leftrightarrow x=4\)
Vậy x = 4
26 tháng 3 2020
a) (3x + 1)^2 - 2(3x + 1)(3x - 5) + (3x - 5)^2
= 9x^2 + 6x + 1 - 18x^2 + 24x + 10 + 9x^2 - 30x + 25
= 36
b) (3x^2 - y)^2
= 9x^4 - 6x^2y + y^2
c) (3x + 5)^2 + (3x - 5)^2 - (3x + 2)(3x - 2)
= 9x^2 + 30x + 25 + 9x^2 - 30x + 25 - 9x^2 + 4
= 9x^2 + 54
d) 2x(2x - 1)^2 - 3x(x + 3)(x - 3) - 4x(x + 1)^2
= 8x^3 - 8x^2 + 2x - 3x^2 + 27x - 4x^3 - 8x^2 - 4x
= x^3 - 16x^2 + 25x
e) (x - 2)(x^2 + 2x + 4) - (x + 1)^2 + 3(x - 1)(x + 1)
= x^3 - 8 - x^2 - 2x - 1 + 3x^2 - 2
= x^3 + 2x^2 - 2x - 12
f) (x^4 - 5x^2 + 25)(x^2 + 5) - (2 + x^2)^2 + 3(1 + x^2)^2
= x^6 + 125 - 4 - 4x^2 - x^2 + 3 + 6x^2 + 3x^4
= x^6 + 2x^4 + 2x^2 + 124
26 tháng 1 2021
a, làm tương tự với phần b bài nãy bạn đăng
b, \(\left(x+1\right)^2-5=x^2+11\)
\(\Leftrightarrow x^2+2x+1-5=x^2+11\)
\(\Leftrightarrow2x-10=0\Leftrightarrow x=5\)
Vậy tập nghiệm của phương trình là S = { 5 } ( kết luận như thế với các phần sau nhé ! )
c, \(3\left(3x-1\right)=3x+5\Leftrightarrow9x-3-3x-5=0\)
\(\Leftrightarrow6x-8=0\Leftrightarrow x=\frac{4}{3}\)
d, \(3x\left(2x-3\right)-3\left(3+2x^2\right)=0\)
\(\Leftrightarrow6x^2-9x-9-6x^2=0\Leftrightarrow-9x=9\Leftrightarrow x=-1\)
e, khai triển nó ra rút gọn rồi giải thôi nhé! ( tự làm )
f, \(\left(x-1\right)^2-x\left(x+1\right)+3\left(x-2\right)+5=0\)
\(\Leftrightarrow x^2-2x+1-x^2+x+3x-6+5=0\)
\(\Leftrightarrow2x=0\Leftrightarrow x=\frac{0}{2}\)vô lí
Vậy phương trình vô nghiệm
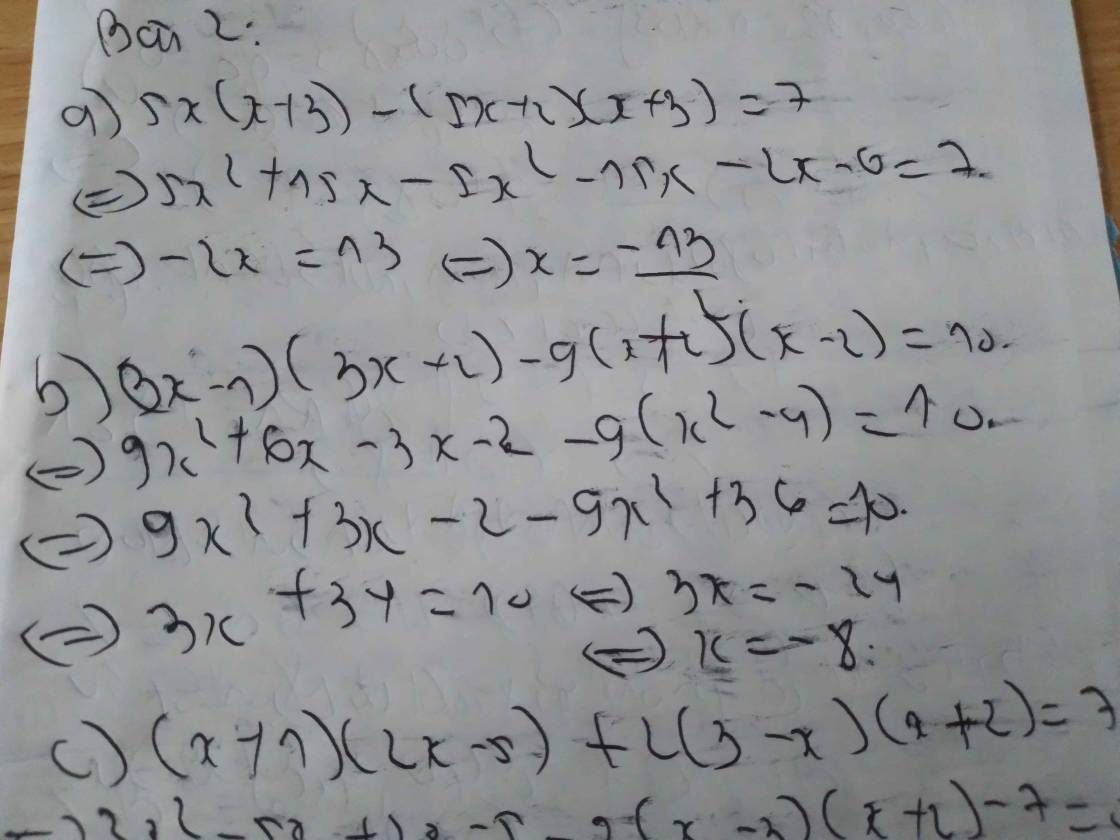
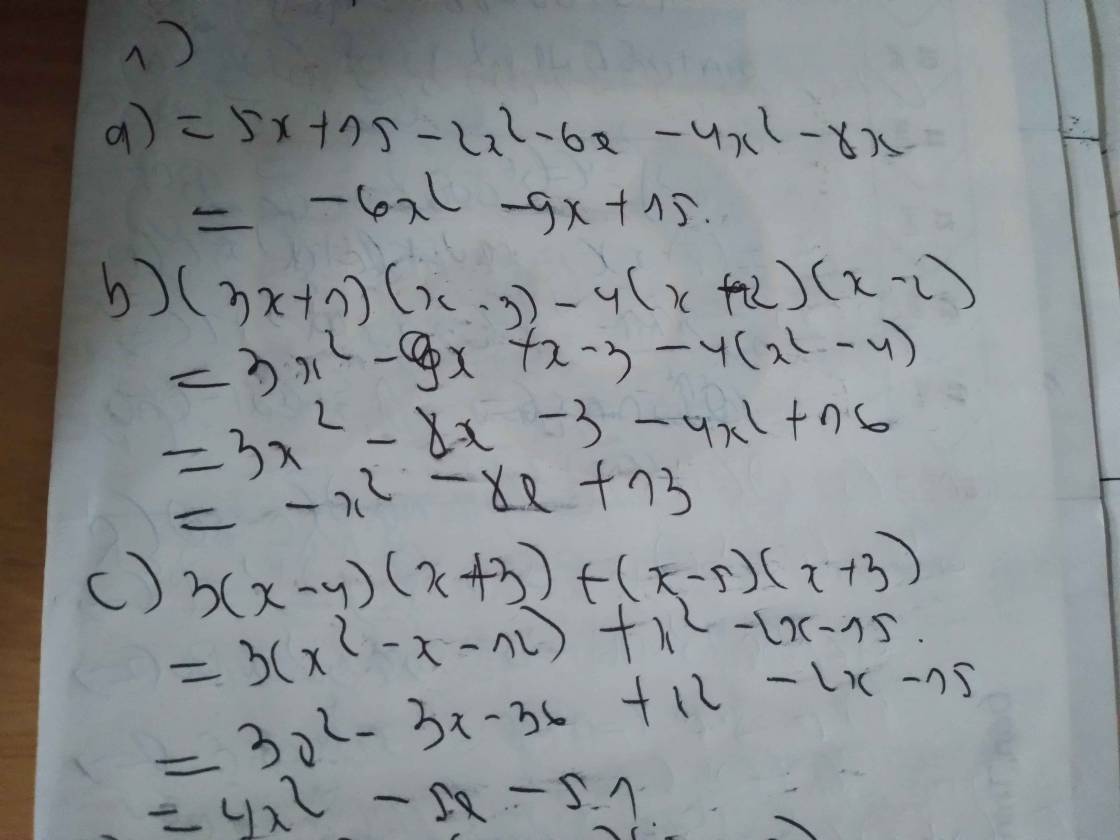
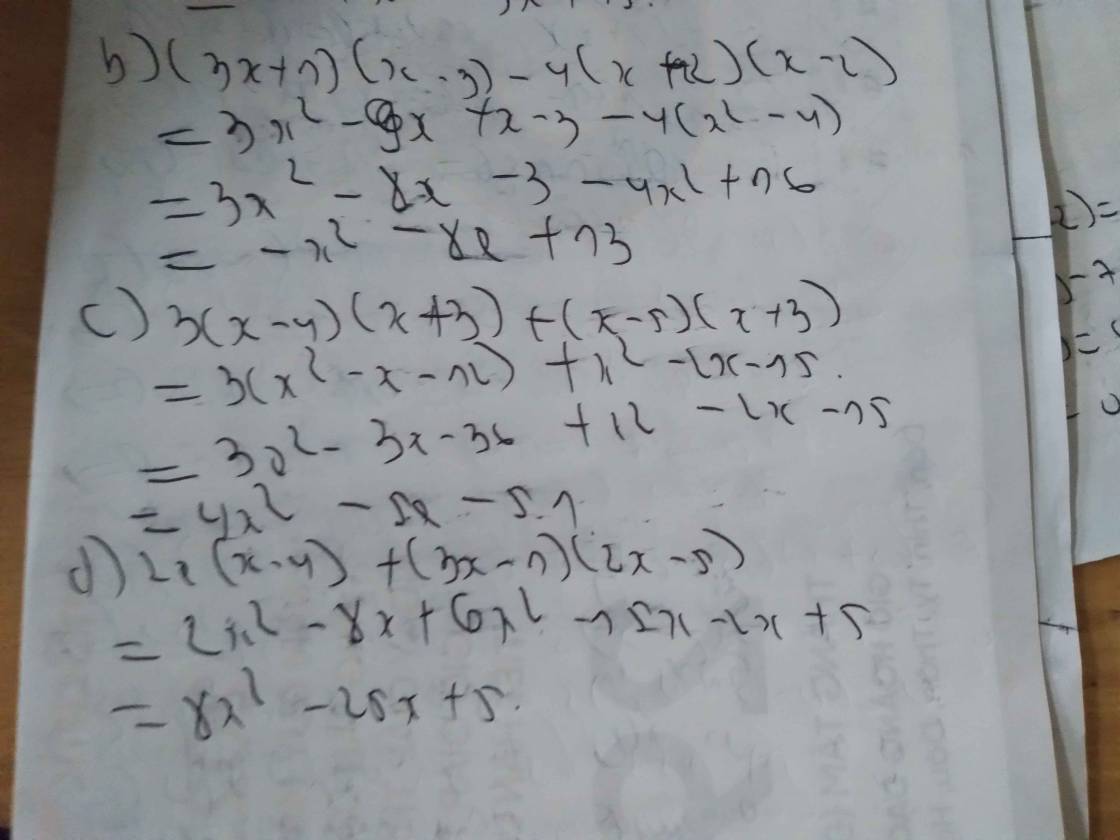
(x+1)3−(x3+3x)=−5 \(x^{3} + 3 x^{2} + 3 x + 1 - x^{3} - 3 x = - 5\) \(3 x^{2} + 1 = - 5 \Rightarrow 3 x^{2} = - 6 \Rightarrow x^{2} = - 2\)
Vì \(x^{2} = - 2\) không có nghiệm thực ⇒ Phương trình vô nghiệm.
\(\left(x+1\right)^3-\left(x^3+3x\right)=-5\)
=>\(x^3+3x^2+3x+1-x^3-3x=-5\)
=>\(3x^2+1=-5\)
=>\(3x^2=-6\)
=>\(x^2=-2\) (vô lý)
=>x∈∅