em cám ơn cô
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
TK
2
Những câu hỏi liên quan
PK
0
CH
Cô Hoàng Huyền
Admin
VIP
1 tháng 11 2016
Tính chất đối xứng - Toán lớp 8 [Online Math - olm.vn] - YouTube
Em có thể xem bài giảng tại đây nhé, ở đó cô đã trình bày rõ hai loại đối xứng tâm và đối xứng trục.
PK
0
13 tháng 2 2022
-Vì bài dài quá nên mình nói tóm tắt:
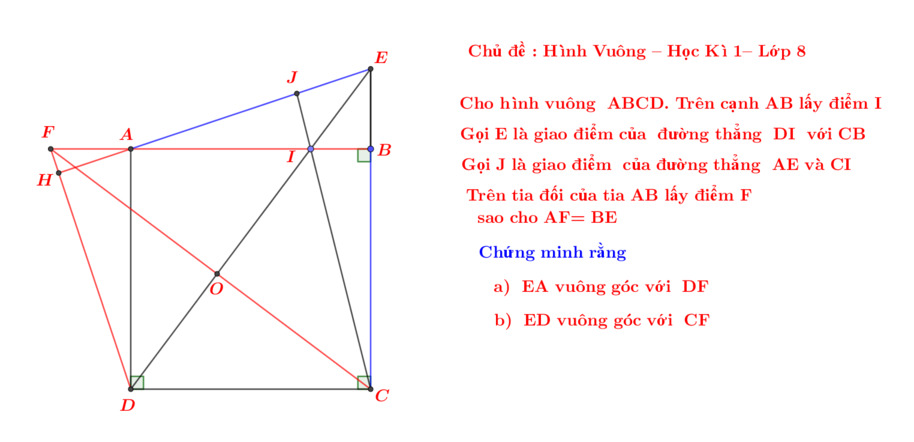
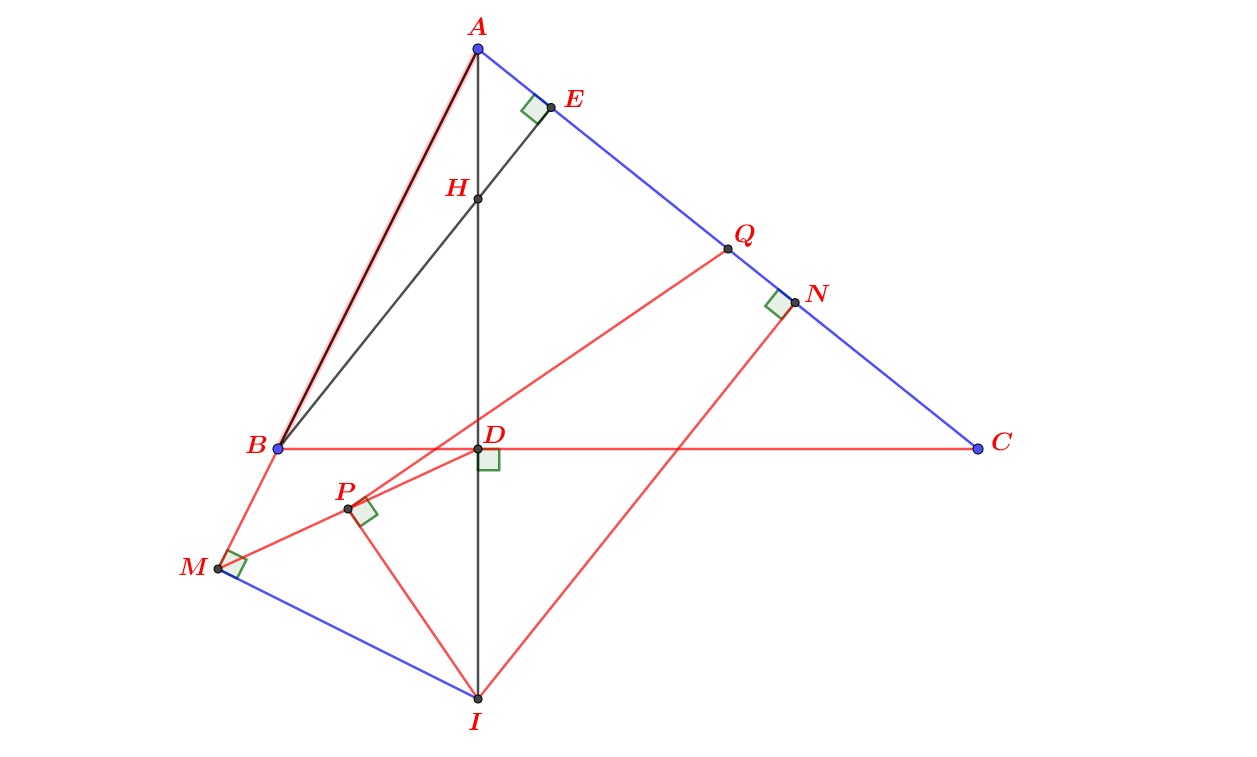
a) -Bạn chứng minh △ABM = △BCN (g-c-g) do có \(AB=BC\) , \(\widehat{BCN}=\widehat{ABM}=90^0\),\(\widehat{NBC}=\widehat{MAB}\) (bạn tự chứng minh).
-Suy ra: \(BM=CN\) .
-Suy ra 2 điều:
+\(QM^2-BQ^2=MN^2-MC^2\)
+\(QM+BQ=MN+MC\) (1)
\(QM^2-BQ^2=MN^2-MC^2\)
\(\Rightarrow\left(QM-BQ\right)\left(QM+BQ\right)=\left(MN-MC\right)\left(MN+MC\right)\)
\(\Rightarrow QM-BQ=MN-MC\) (2)
-Từ (1),(2) suy ra \(QM=MN\) nên △BMQ=△CNM (ch-cgv).
\(\Rightarrow\) MQ vuông góc với MN (bạn tự c/m).
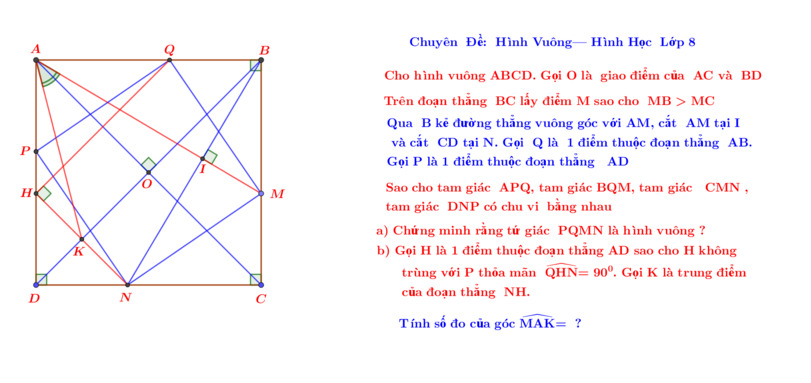
\(QM=MN\) nên \(BQ=MC\) nên \(AQ=BM\Rightarrow PQ^2-AP^2=QM^2-BQ^2;QM+BQ=PQ+AP\)
Nên \(PQ=QM;\Delta APQ=\Delta BQM\) nên PQ⊥QM ; AP=BQ nên PQ=AQ
-Từ PQ=AQ bạn tự c/m PN=PQ (theo sườn mình đã cho) rồi sau đó c/m tam giác APQ=tam giác DNP rồi từ đó suy ra PQ vuông góc PN
.......
PK
0
cô Hoài ns đúng đó bn cs thể vào đây học nhiều hơn để nhận thêm nhiều bài học hay và tình cảm của mn dành cho bn!
Olm chào em. Khi nhận được sự dạy dỗ, bảo ban, quan tâm giúp đỡ hỗ trợ, người biết nói cảm ơn luôn thành công hơn người khác.
Chúc em học tập hiệu quả và vui vẻ cùng Olm cảm ơn em đã đồng hành cùng olm trên hành trình tri thức.