Question

[dảk dảk bruh bruh lmao]

kẻ hình và gải

Answer 1

[Nguyễn Lê Phước Thịnh]

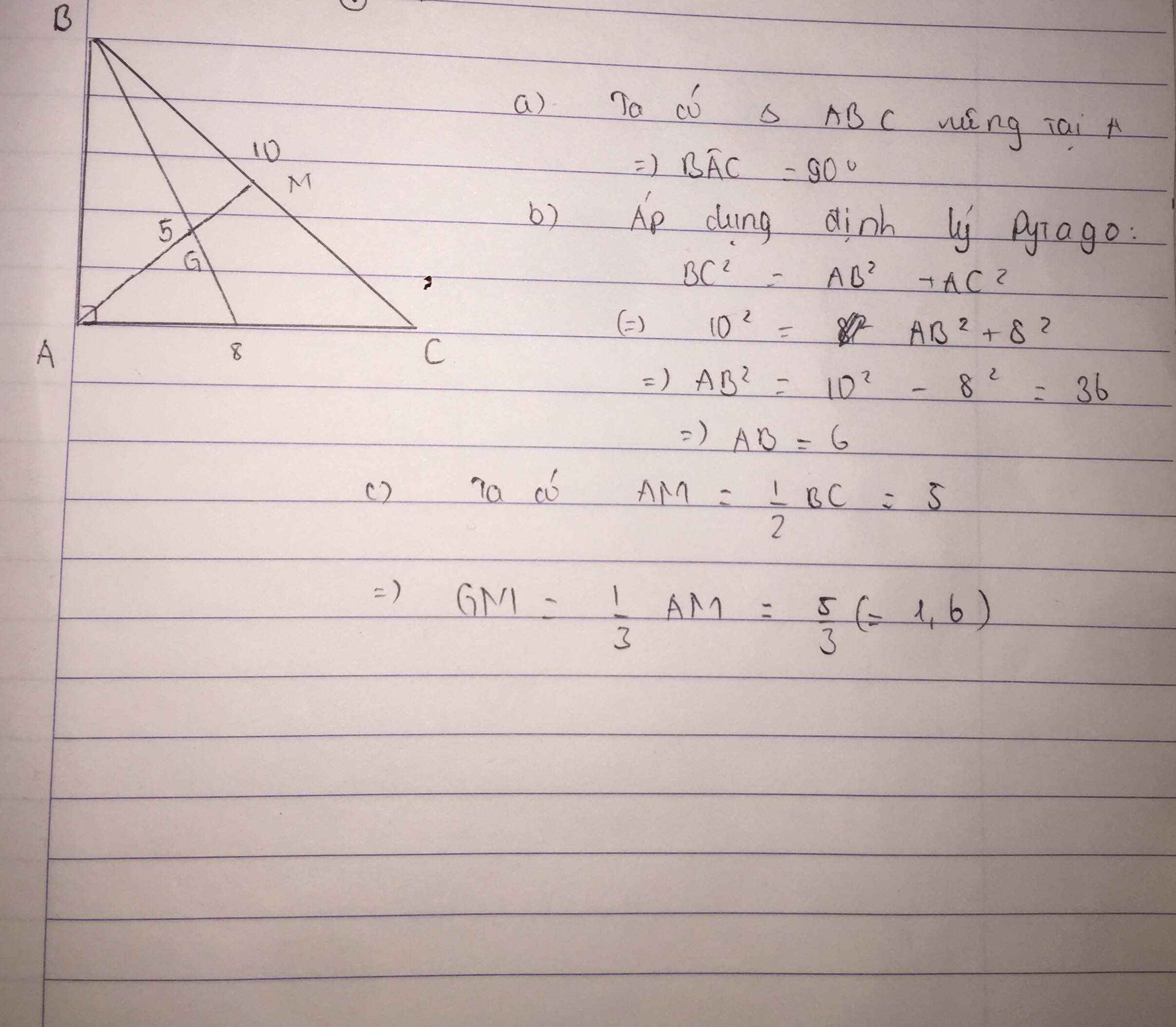
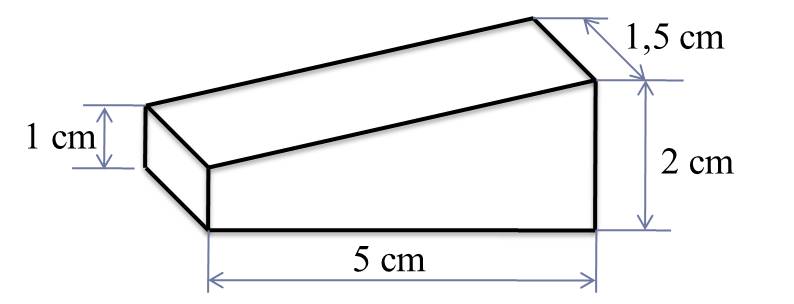
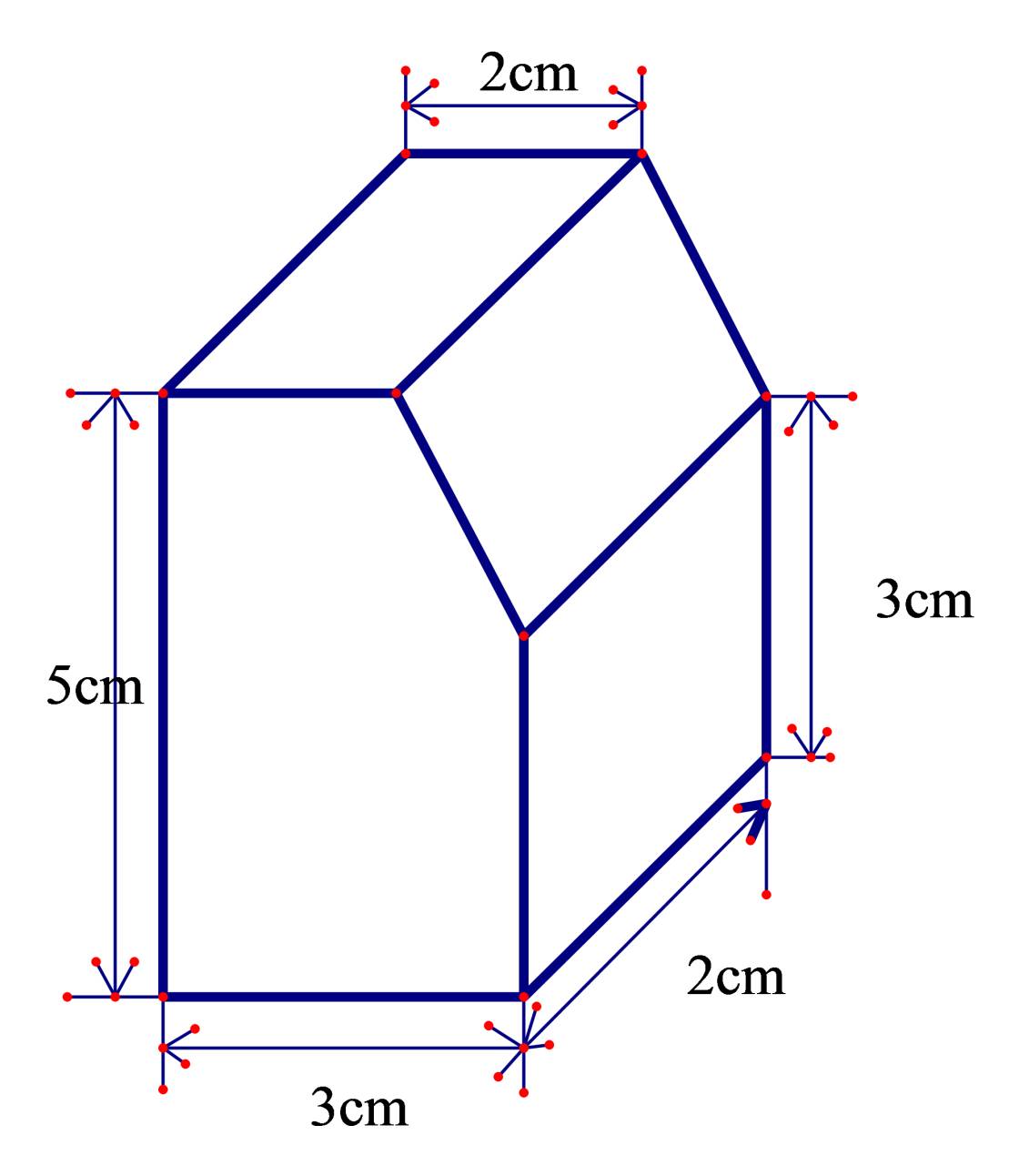
Bài 5:

a: ΔABC cân tại A

mà AM là đường trung tuyến

nên AM⊥BC tại M

Xét tứ giác AMCK có

I là trung điểm chung của AC và MK

=>AMCK là hình bình hành

Hình bình hành AMCK có \(\hat{AMC}=90^0\)

nên AMCK là hình chữ nhật

b: ta có: AMCK là hình chữ nhật

=>AK//CM và AK=CM

AK//CM

=>AK//BM

Ta có: AK=CM

BM=CM

Do đó: AK=BM

Xét tứ giác AKMB có

AK//MB

AK=MB

Do đó: AKMB là hình bình hành

c: Xét tứ giác ABEC có

M là trung điểm chung của AE và BC

=>ABEC là hình bình hành

Hình bình hành ABEC có AB=AC

nên ABEC là hình thoi

Bài 6:

a: ta có: \(BE=EC=\frac{BC}{2}\)

\(FA=FD=\frac{AD}{2}\)

\(AB=CD=\frac{BC}{2}\)

mà AD=BC(ABCD là hình bình hành)

nên BE=EC=FA=FD=AB=CD

Xét tứ giác ABEF có

BE//AF

BE=AF

Do đó: ABEF là hình bình hành

Hình bình hành ABEF có BE=BA

nên ABEF là hình thoi

=>BF⊥AE

b: Xét ΔBAF có AB=AF và \(\hat{BAF}=60^0\)

nên ΔBAF đều

=>\(\hat{ABF}=\hat{AFB}=60^0\)

Ta có: BC//AD

=>\(\hat{BFA}=\hat{FBC}\) (hai góc so le trong)

=>\(\hat{FBC}=60^0\)

ABCD là hình bình hành

=>\(\hat{BAD}=\hat{BCD}\)

=>\(\hat{BCD}=60^0\)

Xét tứ giác BCDF có

BC//DF

\(\hat{FBC}=\hat{DCB}\left(=60^0\right)\)

Do đó: BCDF là hình thang cân

c: Ta có; BA=CD

BA=BM

Do đó: BM=CD

Ta có: BA//CD

=>BM//CD

Ta có: ΔABF đều

=>BF=FA=AD/2

Xét ΔABD có

BF là đường trung tuyến

\(BF=\frac{AD}{2}\)

Do đó: ΔABD vuông tại B

=>BD⊥BA tại B

=>BD⊥MA tại B

Xét tứ giác BDCM có

BM//CD
BM=CD

Do đó: BDCM là hình bình hành

Hình bình hành BDCM có BD⊥BM

nên BDCM là hình chữ nhật

d: Ta có: BDCM là hình chữ nhật

=>BC cắt DM tại trung điểm của mỗi đường

mà E là trung điểm của BC

nên E là trung điểm của DM

=>M,E,D thẳng hàng

Bài 7:

a: Ta có: AK=KI=IH

mà AK+KI+IH=AH

nên \(AK=KI=IH=\frac{AH}{3}\)

Xét ΔAHB có MK//BH

nên \(\frac{AK}{AH}=\frac{AM}{AB}\)

=>\(\frac{AM}{AB}=\frac13\)

Xét ΔAHB có EI//BH

nên \(\frac{AI}{AH}=\frac{AE}{AB}\)

=>\(\frac{AE}{AB}=\frac23\)

Xét ΔACB có MN//BC

nên \(\frac{MN}{BC}=\frac{AM}{AB}=\frac13\)

=>\(MN=\frac{BC}{3}=5\left(\operatorname{cm}\right)\)

Xét ΔACB có EF//BC

nên \(\frac{EF}{CB}=\frac{AE}{AB}=\frac23\)

=>\(EF=CB\cdot\frac23=15\cdot\frac23=10\left(\operatorname{cm}\right)\)

b: Xét ΔAEF và ΔABC có

\(\hat{AEF}=\hat{ABC}\) (hai góc đồng vị, EF//BC)

\(\hat{BAC}\) chung

Do đó: ΔAEF~ΔABC

=>\(\frac{S_{AEF}}{S_{ABC}}=\left(\frac{AE}{AB}\right)^2=\frac49\)

=>\(S_{AEF}=270\cdot\frac49=120\left(\operatorname{cm}^2\right)\)

Xét ΔAMN và ΔAEF có

\(\hat{AMN}=\hat{AEF}\) (hai góc đồng vị, MN//EF)

\(\hat{MAN}\) chung

Do đó: ΔAMN~ΔAEF

=>\(\frac{S_{AMN}}{S_{AEF}}=\left(\frac{AM}{AE}\right)^2=\left(\frac12\right)^2=\frac14\)

=>\(S_{AMN}=S_{AEF}\cdot\frac14=\frac{120}{4}=30\left(\operatorname{cm}^2\right)\)

Ta có: \(S_{AMN}+S_{MNFE}=S_{AEF}\)

=>\(S_{MNFE}=120-30=90\left(\operatorname{cm}^2\right)\)