Rút gọn
B=-1+1/2-1/2^2+...-1/2^2n+1/2^2n+1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KT
4 tháng 1 2018
\(B=\frac{1^2}{2^2-1}.\frac{3^2}{4^2-1}.\frac{5^2}{6^2-1}...\frac{\left(2n+1\right)^2}{\left(2n+2\right)^2-1}\)
\(=\frac{1^2}{\left(2-1\right)\left(2+1\right)}.\frac{3^2}{\left(4-1\right)\left(4+1\right)}...\frac{\left(2n+1\right)^2}{\left(2n+2-1\right)\left(2n+2+1\right)}\)
\(=\frac{1}{1.3}.\frac{3^2}{3.5}...\frac{\left(2n+1\right)^2}{\left(2n+1\right)\left(2n+3\right)}\)
\(=\frac{1}{2n+3}\)
TP
1
NX
1
8 tháng 4 2021
Đề có phải là \(\dfrac{1}{2\sqrt{x}}-\dfrac{1}{2\sqrt{x}}+\dfrac{2-\sqrt{x}}{1-x}\) không bạn?
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 12 2020
Xét khai triển:
\(\left(1+2x\right)^{2n+1}=C_{2n+1}^0+C_{2n+1}^1.2x+C_{2n+1}^2\left(2x\right)^2+...+C_{2n+1}^{2n+1}\left(2x\right)^{2n+1}\)
Đạo hàm 2 vế:
\(2\left(2n+1\right)\left(1+2x\right)^{2n}=2C_{2n+1}^1+2^2C_{2n+1}^2x+...+\left(2n+1\right)2^{2n+1}C_{2n+1}^{2n+1}x^{2n}\)
\(\Leftrightarrow\left(2n+1\right)\left(1+2x\right)^{2n}=C_{2n+1}^1+2C_{2n+1}^2x+...+\left(2n+1\right)2^{2n}C_{2n+1}^{2n+1}x^{2n}\)
Cho \(x=-1\) ta được:
\(2n+1=C_{2n+1}^1-2C_{2n+1}^2+...+\left(2n+1\right)2^{2n}C_{2n+1}^{2n+1}\)
\(\Rightarrow2n+1=2019\Rightarrow n=1009\)
G
6 tháng 8 2023
a. ĐK: \(x\ne\pm2\)
\(M=\left[\dfrac{x\left(x+2\right)}{\left(x+2\right)\left(x-2\right)}-\dfrac{\left(x+1\right)\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}-\dfrac{2x+7}{\left(x-2\right)\left(x+2\right)}\right]:\dfrac{3-x+x-2}{x-2}\)
\(=\dfrac{x^2+2x-\left(x^2-2x+x-2\right)-2x-7}{\left(x-2\right)\left(x+2\right)}.\left(x-2\right)\)
\(=\dfrac{x-5}{x+2}\)
b. \(\dfrac{x-5}{x+2}< 1\Leftrightarrow\dfrac{x-5}{x+2}-1< 0\)
\(\Leftrightarrow\dfrac{-7}{x+2}< 0\Leftrightarrow x+2>0\)
\(\Leftrightarrow x>-2\)
Vậy \(x>-2,x\ne2\)
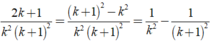
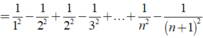
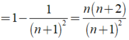
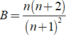
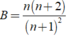
chịu r
\(B=-1+\frac12-\frac{1}{2^2}+\cdots-\frac{1}{2^{2n}}+\frac{1}{2^{2n+1}}\)
=>\(2B=-2+1-\frac12+\cdots-\frac{1}{2^{2n-1}}+\frac{1}{2^{2n}}\)
=>\(2B+B=-2+1-\frac12+\cdots-\frac{1}{2^{2n-1}}+\frac{1}{2^{2n}}-1+\frac12-\frac{1}{2^2}+\cdots-\frac{1}{2^{2n}}+\frac{1}{2^{2n+1}}\)
=>\(3B=-2+\frac{1}{2^{2n+1}}=\frac{-2^{2n+2}+1}{2^{2n+1}}\)
=>\(B=\frac{-2^{2n+2}+1}{3\cdot2^{2n+1}}\)