Bài 6. Cho hình thang ABCD có đáy AB = 3/7 CD. Nối A với C; B với D, chúng cắt nhau tại M. Biết diện tích hình tam giác BMC bằng 50 cm2, tính diện tích hình thang ABCD.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
11 tháng 12 2021
diện tích hình tam giác CMD là:
15 ÷ 4 × 7 = 26,25 (cm2)
diện tích hình tam giác BCD là:
15 + 26,25 = 41,25 (cm2)
Diện tích tam giác ABC là:
41,25 ÷ 7 × 4 = 1657 ( cm2)
Diện tích hình thang ABCD là:
23,57 + 41,25 = 64,82 ( cm2)
Đ/s : 64,82 cm2
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
8 tháng 7 2023
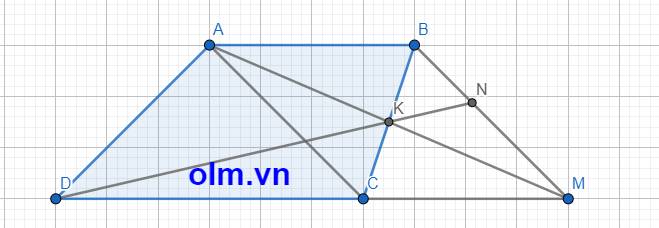
a, Chiều cao hình thang là: (12 + 18): 2 = 15 (cm)
Diện tích hình thang là: (18 + 12)\(\times\)15 : 2 = 225 (cm2)
b, Độ dài đoạn CM là: 18 \(\times\) \(\dfrac{2}{3}\) = 12 (cm)
vậy CM = AB = 12 cm
SABM = SACM vì (hai tam giác có hai đường cao bằng nhau và hai cạnh đáy tương ứng bằng nhau).
Xét tứ giác ABMC có: AB // CM và AB = CM
Nên tứ giác ABMC là hình bình hành
Vì K là giao điểm hai đường chéo của hình bình hành nên K là trung điểm của BC vậy KB = KC
8 tháng 7 2023
Chiều cao của hình thang abcd là:
(18+12):2=15(cm)
a)Diện tích hình thang abcd là:
(18+12)x15:2=225(cm2)
xin lỗi vì mình chỉ giải được phần a thôi!khi nào giải được thì tôi giải tiếp nhé!
11 tháng 5 2016
Do dai day AB cua hinh thang ABCD la :
6 : 3 x 2 = 4 ( cm )
Do dai chieu cao CD cua hinh thang ABCD la :
4 : 2 x 1 = 2 ( cm )
Dien h hinh thang ABCD la :
( 6 + 4 ) x 2 :2 = 10 ( cm2 )
Chieu cao va day CD cua hinh thang ABCD bang chieu cao va do dai day hinh tam giac ACD nen dien h cua hinh tam giac ACD la :
6 x 2 : 2 = 6 ( cm2 )
Chieu cao va day AB cua hinh thang ABCD bang chieu cao va do dai day hinh tam giac ABC nen dien h cua hinh tam giac BCD la :
4 x 2 : 2 = 4 ( cm2 )
Dien h hinh tam giac ACD hon dien h hinh tam giac ABC la :
6 - 4 = 2 ( cm2 )
Dap so : a ) 10 cm2
b ) 2 cm2
c ) 4 cm2
NH
11 tháng 2 2020
Xét tam giác \(ABC\) và tam giác \(ACD\) có \(\frac{AD}{CD}=\frac{4}{7}\) khoảng cách từ \(A\) xuống \(DC\) bằng khoảng cách từ \(C\) xuống \(AB\) nên \(\frac{S_{ABC}}{S_{ACD}}=\frac{4}{7}\)
Xét tam giác \(ABC\) và tam giác \(ACD\) có chung đáy \(AC\)\(\frac{S_{ABC}}{S_{ACD}}=\frac{4}{7}\) nên khoảng cách từ \(B\) đến \(AC\) bằng \(\frac{4}{7}\) khoảng cách từ \(D\) đến \(AC\)
Xét tam giác \(BMC\) và tam giác \(DMC\) có chung đáy \(MC\) khoảng cách từ \(B\)đến \(AC\) bằng\(\frac{4}{7}\) khoảng cách từ \(D\) đến \(AC\) nên \(\frac{S_{BMC}}{S_{CMD}}=\frac{4}{7}\)
Diện tích tam giác \(CMD\) là:
\(15\div4\times7=26,25\)( cm2 )
Diện tích tam giác \(BCD\) là:
\(15+26,25=41,25\)( cm2 )
Diện tích tam giác \(ABC\) là:
\(41,25\div7\times4=\frac{165}{7}=23,57\)( cm2 )
Diện tích hình thang \(ABCD\) là:
\(23,57+41,25=64,82\)( cm2 )
Đáp số : \(64,82\)cm2
19 tháng 3 2020
S tam giác CMD là:
15 : 4.7 = 26,25 (cm2 )
S tam giác BCD là:
15 + 26,25 = 41,25(cm2 )
S tam giác ABC là:
41,25 : 7. 4 = 1657 (cm2 )
S hình thang ABCD là:
23,57 + 41,25 = 64,82(cm2 )
NB
8 tháng 2 2023
*SABC=1/3SABCD(Vì có đáy = đáy bé và có chiều cao=chiều cao hình thang ABCD)
=>SABCD=24x3=72 cm2
Đáp số: 72 cm2
Vì AB//CD
nên \(\frac{MA}{MC}=\frac{MB}{MD}=\frac{AC}{BD}=\frac37\)
Vì \(\frac{AM}{MC}=\frac37\) nên \(\frac{S_{MAB}}{S_{MBC}}=\frac{MA}{MC}=\frac37\)
=>\(S_{AMB}=50\times\frac37=\frac{150}{7}\left(\operatorname{cm}^2\right)\)
Vì \(\frac{BM}{MD}=\frac37\) nên \(\frac{S_{AMB}}{S_{AMD}}=\frac37\)
=>\(S_{AMD}=\frac73\times S_{AMB}=\frac73\times\frac{150}{7}=\frac{150}{3}=50\left(\operatorname{cm}^2\right)\)
Vì \(\frac{MA}{MC}=\frac37\) nên \(\frac{S_{AMD}}{S_{DMC}}=\frac{AM}{MC}=\frac37\)
=>\(S_{DMC}=\frac73\times S_{AMD}=\frac73\times50=\frac{350}{3}\left(\operatorname{cm}^2\right)\)
\(S_{ABCD}=S_{AMB}+S_{BMC}+S_{MCD}+S_{MAD}\)
\(=\frac{150}{7}+50+50+\frac{350}{3}=\frac{5000}{21}\left(\operatorname{cm}^2\right)\)
Vì AB//CD
nên \(\frac{M A}{M C} = \frac{M B}{M D} = \frac{A C}{B D} = \frac{3}{7}\)
Vì \(\frac{A M}{M C} = \frac{3}{7}\) nên \(\frac{S_{M A B}}{S_{M B C}} = \frac{M A}{M C} = \frac{3}{7}\)
=>\(S_{A M B} = 50 \times \frac{3}{7} = \frac{150}{7} \left(\right. \left(cm \right)^{2} \left.\right)\)
Vì \(\frac{B M}{M D} = \frac{3}{7}\) nên \(\frac{S_{A M B}}{S_{A M D}} = \frac{3}{7}\)
=>\(S_{A M D} = \frac{7}{3} \times S_{A M B} = \frac{7}{3} \times \frac{150}{7} = \frac{150}{3} = 50 \left(\right. \left(cm \right)^{2} \left.\right)\)
Vì \(\frac{M A}{M C} = \frac{3}{7}\) nên \(\frac{S_{A M D}}{S_{D M C}} = \frac{A M}{M C} = \frac{3}{7}\)
=>\(S_{D M C} = \frac{7}{3} \times S_{A M D} = \frac{7}{3} \times 50 = \frac{350}{3} \left(\right. \left(cm \right)^{2} \left.\right)\)
\(S_{A B C D} = S_{A M B} + S_{B M C} + S_{M C D} + S_{M A D}\)
\(= \frac{150}{7} + 50 + 50 + \frac{350}{3} = \frac{5000}{21} \left(\right. \left(cm \right)^{2} \left.\right)\)