Cho tỉ lệ thức a/b=c/d.Chứng minh:a^2+b^2/a^2-b^2=c^2+d^2/c^2-d^2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
H
1
DD
Đoàn Đức Hà
Giáo viên
21 tháng 10 2021
Đặt \(\frac{a}{b}=\frac{c}{d}=t\Rightarrow\hept{\begin{cases}a=bt\\c=dt\end{cases}}\).
\(\frac{ac}{bd}=\frac{bt.dt}{bd}=t^2\)
\(\frac{a^2-c^2}{b^2-d^2}=\frac{\left(bt\right)^2-\left(dt\right)^2}{b^2-d^2}=\frac{t^2\left(b^2-d^2\right)}{b^2-d^2}=t^2\)
Suy ra đpcm.
CT
3
2 tháng 11 2019
Ta có: \(\frac{a}{b}=\frac{c}{d}\)
\(\Rightarrow\frac{a^2}{b^2}=\frac{c^2}{d^2}=\frac{ac}{bd}=\frac{a^2-c^2}{b^2-d^2}\)( tính chất của dãy tỉ số bằng nhau )
Vậy ...
M
2 tháng 11 2019
TL :
Đặt \(\frac{a}{b}=\frac{c}{d}=k\Rightarrow a=bk;c=dk\)
=> Vế trái \(=\frac{ac}{bd}=\frac{bkdk}{bd}=k^2\)
=> Vế phải \(=\frac{a^2+c^2}{b^2+d^2}=\frac{b^2k^2+d^2k^2}{b^2+d^2}=\frac{k^2.\left(b^2+d^2\right)}{b^2+d^2}=k^2\)
\(\Rightarrow\)Vế trái = Vế phải
\(\Rightarrowđpcm\)
6 tháng 11 2019
*\(\frac{a}{b}=\frac{c}{d}\)=> \(\frac{a^2}{b^2}=\frac{c^2}{d^2}=\frac{a^2-c^2}{b^2-d^2}=\frac{a}{b}.\left(\frac{a}{b}\right)=\frac{ac}{bd}\)(đpcm)
* \(\frac{a}{b}=\frac{c}{d}=\frac{a+c}{b+d}\)=> \(\frac{a^2}{b^2}=\frac{c^2}{d^2}=\left(\frac{a+c}{b+d}\right)^2\)(1)
Ta lại có \(\frac{a}{b}=\frac{c}{d}\)=>\(\frac{a^2}{b^2}=\frac{c^2}{d^2}=\frac{a^2+c^2}{b^2+d^2}\)(2)
Từ (1),(2) => đpcm
T
30 tháng 7 2019
#)Giải :
Ta có : \(\frac{a}{b}=\frac{c}{d}\Rightarrow\frac{a}{c}=\frac{b}{d}\Rightarrow\frac{a^2}{c^2}=\frac{b^2}{d^2}=\frac{a^2+b^2}{c^2+d^2}=\frac{a^2-b^2}{c^2-d^2}\left(1\right)\)
Lại có : \(\frac{a^2}{c^2}=\frac{b^2}{d^2}=\left(\frac{a}{c}\right)^2=\left(\frac{b}{d}\right)^2=\left(\frac{a+b}{c+d}\right)^2=\frac{\left(a+b\right)^2}{\left(c+d\right)^2}\left(2\right)\)
\(\Rightarrowđpcm\)
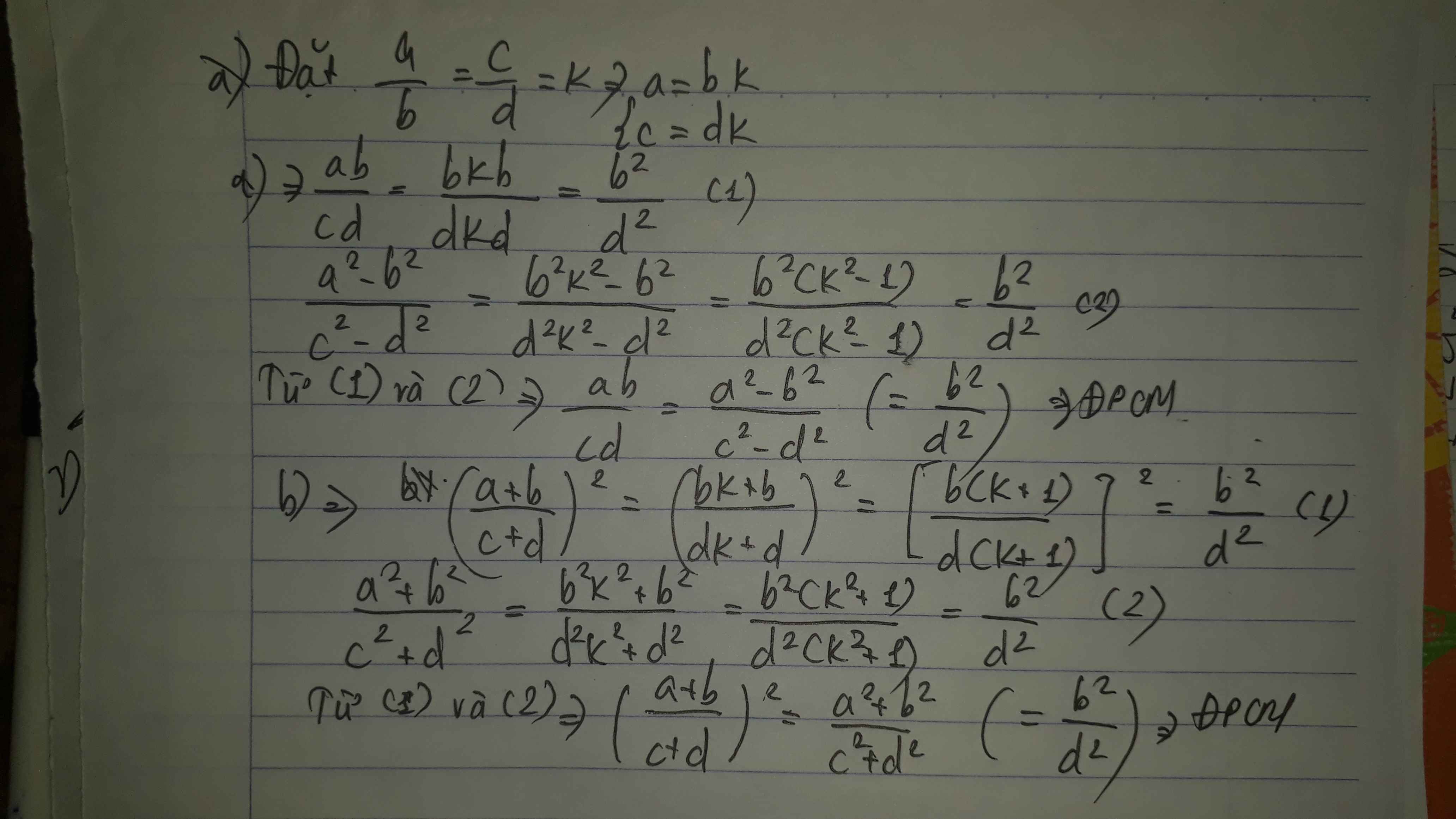
Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\)
=>a=bk; c=dk
\(\dfrac{a^2+b^2}{a^2-b^2}=\dfrac{\left(bk\right)^2+b^2}{\left(bk\right)^2-b^2}=\dfrac{b^2\left(k^2+1\right)}{b^2\left(k^2-1\right)}=\dfrac{k^2+1}{k^2-1}\)
\(\dfrac{c^2+d^2}{c^2-d^2}=\dfrac{\left(dk\right)^2+d^2}{\left(dk\right)^2-d^2}=\dfrac{d^2\left(k^2+1\right)}{d^2\left(k^2-1\right)}=\dfrac{k^2+1}{k^2-1}\)
Do đó: \(\dfrac{a^2+b^2}{a^2-b^2}=\dfrac{c^2+d^2}{c^2-d^2}\)
Ta cần chứng minh bất đẳng thức sau từ tỉ lệ thức \(\frac{a}{b} = \frac{c}{d}\), tức là \(a d = b c\):
\(\frac{a^{2} + b^{2}}{a^{2} - b^{2}} = \frac{c^{2} + d^{2}}{c^{2} - d^{2}}\)
Bước 1: Sử dụng tỉ lệ thức \(\frac{a}{b} = \frac{c}{d}\)
Từ tỉ lệ thức \(\frac{a}{b} = \frac{c}{d}\), ta có:
\(a d = b c\)
Bước 2: Biến đổi phương trình cần chứng minh
Ta muốn chứng minh rằng:
\(\frac{a^{2} + b^{2}}{a^{2} - b^{2}} = \frac{c^{2} + d^{2}}{c^{2} - d^{2}}\)
Để làm điều này, ta sẽ tìm cách viết lại các biểu thức này sao cho chúng trở nên tương đương.
Bước 3: Sử dụng phép nhân chéo để chứng minh
Ta nhân chéo các vế trong phương trình:
\(\left(\right. a^{2} + b^{2} \left.\right) \left(\right. c^{2} - d^{2} \left.\right) = \left(\right. c^{2} + d^{2} \left.\right) \left(\right. a^{2} - b^{2} \left.\right)\)
Bây giờ, ta sẽ mở rộng hai vế:
Như vậy, phương trình trở thành:
\(a^{2} c^{2} - a^{2} d^{2} + b^{2} c^{2} - b^{2} d^{2} = c^{2} a^{2} - c^{2} b^{2} + d^{2} a^{2} - d^{2} b^{2}\)
Bước 4: So sánh các hạng tử
Ta có thể thấy rằng các hạng tử ở cả hai vế là giống nhau, chỉ khác vị trí. Do đó, ta có thể khẳng định rằng hai vế này là tương đương.
Vậy, ta đã chứng minh được:
\(\frac{a^{2} + b^{2}}{a^{2} - b^{2}} = \frac{c^{2} + d^{2}}{c^{2} - d^{2}}\)
Do đó, ta đã chứng minh được đẳng thức cần chứng minh.