Cho A=(-1,1) B(2,3) C(1,4)
a) phương trình đường trung trực cạnh AB
b)phương trình cạnh AC
c)phương trình đường trung bình ứng với cạnh BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AT
16 tháng 7 2021
a) Gọi pt đường thẳng AB là \(y=ax+b\)
\(\Rightarrow\left\{{}\begin{matrix}1=a+b\\-1=b\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}a=2\\b=-1\end{matrix}\right.\Rightarrow y=2x-1\)
b) Thế \(C\left(2;3\right)\) vào pt đường thẳng AB thì ta thấy \(3=2.2-1\)
\(\Rightarrow C\in\) đường thẳng AB \(\Rightarrow A,B,C\) thẳng hàng
1 tháng 4 2016
a) Gọi M là trung điểm cạnh CA thì \(M\left(\frac{3}{2};1\right)\) và \(\overrightarrow{BM}=\left(\frac{9}{2};-3\right)\).
Đường trung tuyến BM của tam giác có vec tơ chỉ phương \(\overrightarrow{u}=\frac{2}{3}.\overrightarrow{BM}=\left(3;-2\right)\) suy ra ta có phương trình
\(\frac{x+3}{3}=\frac{y-4}{-2}\)
b) Do đường cao kẻ từ A có phương vuông góc với đường thẳng BC nên nó nhận \(\overrightarrow{BC}=\left(5;-4\right)\) làm vec tơ pháp tuyến. Suy ra có phương trình.
\(5.\left(x-1\right)-4\left(y-2\right)=0\) hay \(5x-4y+3=0\)
c) Ta có \(\overrightarrow{AB}=\left(-4;2\right)=2.\left(-2;1\right)\). Gọi N là trung điểm AC thì N(-1;3)
Đường trung trực của cạnh AB đi qua N(-1;3) và có vec tơ pháp tuyến
\(\overrightarrow{n}=\frac{1}{2}.\overrightarrow{AB}=\left(-2;1\right)\)
Suy ra có phương trình
\(-2.\left(x+1\right)+1.\left(y-3\right)=0\) hay \(-2x+y-5=0\)
7 tháng 3 2024
bạn ơi trên −−→BM=(92;−3)��→=(92;−3)
dưới −−→BM=(3;−2) là sao bạn
30 tháng 6 2023
a: vecto AB=(1;-1)
=>VTPT là (1;1)
Phương trình AB là:
1(x-0)+1(y-3)=0
=>x+y-3=0
vecto AC=(-3;2)
=>VTPT là (2;3)
Phương trình AC là:
2(x-0)+3(y-3)=0
=>2x+3y-9=0
vecto BC=(-4;3)
=>VTPT là (3;4)
Phương trình BC là;
3(x-1)+4(y-2)=0
=>3x-3+4y-8=0
=>3x+4y-11=0
vecto BC=(-4;3)
=>AH có VTPT là (-4;3)
Phương trình AH là;
-4(x-0)+3(y-3)=0
=>-4x+3y-9=0
b: vecto AC=(-3;2)
=>BK có VTPT là (-3;2)
Phương trình BK là:
-3(x-1)+2(y-2)=0
=>-3x+3+2y-4=0
=>-3x+2y-1=0
Tọa độ K là:
-3x+2y-1=0 và -4x+3y-9=0
=>K(15;23)
d: vecto AB=(1;-1)
=>Đường trung trực của AB có VTPT là (1;-1)
Tọa độ N là trung điểm của AB là:
x=(0+1)/2=1/2 và y=(2+3)/2=2,5
Phương trình đường trung trực của AB là:
1(x-0,5)+(-1)(y-2,5)=0
=>x-y+2=0
14 tháng 4 2023
vecto AB=(-4;4)=(-1;1)
Tọa độ trung điểm của AB là:
x=(-1-5)/2=-6/2=-3 và y=(-1+3)/2=1
Phương trình trung trực của AB là:
-1(x+3)+1(y-1)=0
=>-x-3+y-1=0
=>-x+y-4=0
CM
17 tháng 11 2017
Đáp án: B
Gọi I là trung điểm của AB ⇒ I(0;-1)
A(1;-3), B(-1;1)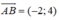 
Đường thẳng trung trực của AB là đường thẳng đi qua I và nhận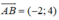 
là vecto pháp tuyến: -2(x - 0) + 4(y + 1) = 0 ⇔ x - 2y - 2 = 0
KC
1
AH
Akai Haruma
Giáo viên
28 tháng 1 2024
Lời giải:
$\overrightarrow{AB}=(2,-6)$
PT đường trung trực của $AB$ gọi là $(d)$.
$(d)\perp AB\Rightarrow VTPT(d) = \overrightarrow{AB}=(2,-6)$
$\Rightarrow VTCP(d) = (6,2)$ (1)
$(d)$ đi qua trung điểm của $AB$ là $(2,-1)$ (2)
Từ (1); (2)$ suy ra PTTS của $(d)$ là: \(\left\{\begin{matrix} x=2+6t\\ y=-1+2t\end{matrix}\right.\)
a: Tọa độ trung điểm I của AB là:
\(\left\{{}\begin{matrix}x=\dfrac{-1+2}{2}=\dfrac{1}{2}\\y=\dfrac{1+3}{2}=\dfrac{4}{2}=2\end{matrix}\right.\)
=>I(1/2;2)
A(-1;1); B(2;3)
=>\(\overrightarrow{AB}=\left(2+1;3-1\right)\)
=>\(\overrightarrow{AB}=\left(3;2\right)\)
Gọi d là đường trung trực của AB
mà I là trung điểm của AB
nên d\(\perp\)AB tại I
d\(\perp\)AB nên d nhận \(\overrightarrow{AB}=\left(3;2\right)\) làm vecto pháp tuyến
Phương trình d là:
\(3\left(x-\dfrac{1}{2}\right)+2\left(y-2\right)=0\)
=>\(3x+2y-\dfrac{11}{2}=0\)
b: \(A\left(-1;1\right);C\left(1;4\right)\)
=>\(\overrightarrow{AC}=\left(1+1;4-1\right)=\left(2;3\right)\)
=>AC có vecto pháp tuyến là (-3;2)
Phương trình đường thẳng AC là:
-3(x+1)+2(y-1)=0
=>-3x-3+2y-2=0
=>-3x+2y-5=0
c: Tọa độ trung điểm M của AC là:
\(\left\{{}\begin{matrix}x=\dfrac{-1+1}{2}=\dfrac{0}{2}=0\\y=\dfrac{1+4}{2}=\dfrac{5}{2}\end{matrix}\right.\)
Xét ΔABC có
I,M lần lượt là trung điểm của AB,AC
=>IM là đường trung bình của ΔABC
=>IM//BC
I(1/2;2) M(0;5/2)
\(\overrightarrow{IM}=\left(0-\dfrac{1}{2};\dfrac{5}{2}-2\right)=\left(-\dfrac{1}{2};\dfrac{1}{2}\right)=\left(-1;1\right)\)
=>IM có vecto pháp tuyến là (1;1)
Phương trình đường trung bình ứng với cạnh BC là:
1(x-0)+1(y-5/2)=0
=>\(x+y-\dfrac{5}{2}=0\)